참조: https://junstar92.tistory.com/197
참조: https://freedeveloper.tistory.com/390
참조: https://sexy-developer.tistory.com/56
1. 위상 정렬이란?
사이클이 없는 방향 그래프(DAG 또는 방향 비순환 그래프)의 모든 노드를 방향성에 거스르지 않도록 순서ㅐ로 나열하는 것을 의미한다.(시간 복잡도: O(V+E))
예시) 인물 캐스팅 그래프
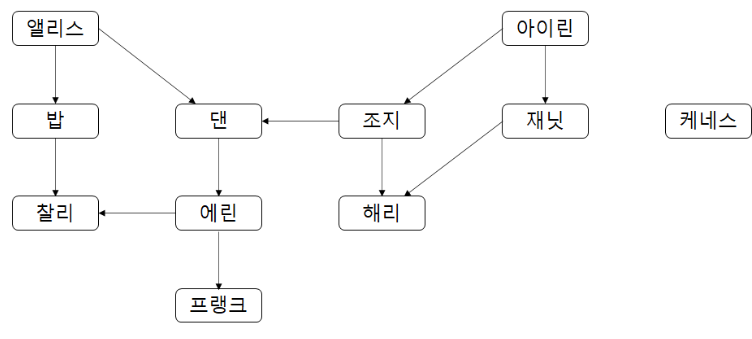
- 이 그래프에서 위상 정렬을 한다고 했을 때, 위상 정렬은 이미 앞에 있는 사람들에게 연락했을 때만 뒤의 누군가에게 연락하는 데 사용할 수 있는 사람들의 순서.(어떤 사람에게 마지막으로 연락할 것인가를 생각하면 된다.)
- 마지막으로 연락할 사람의 후보로는 찰리, 프랭크, 해리, 케네스가 있다.
- 마지막으로 연락할 사람을 찾았으면, 이 사람 전에 누구에게 연락할 것인지 찾으면 되는 방식.
- 예를 들어 마지막 사람으로 프랭크를 선택했다면 찰리, 해리, 케네스가 후보로 남는다. 그 후 찰리를 선택했다고 가정하면, 마지막으로 프랭크에게 연락하고 프랭크 전에 찰리한테 연락하는 순서를 가진다.
2. 위상 정렬 방법
- 큐를 이용한 위상 정렬
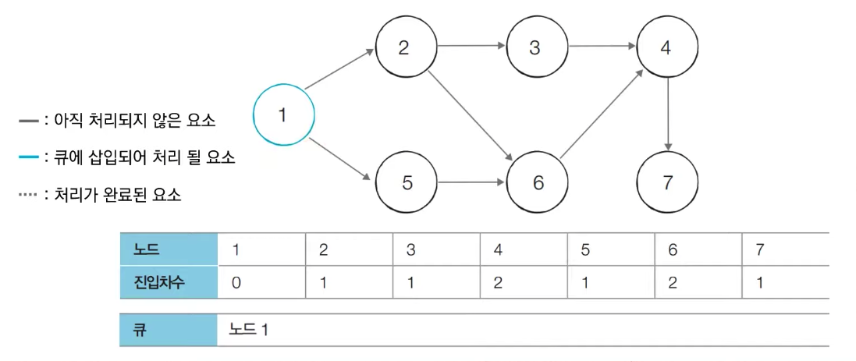
- 진입 차수가 0인 모든 노드를 큐에 넣는다.
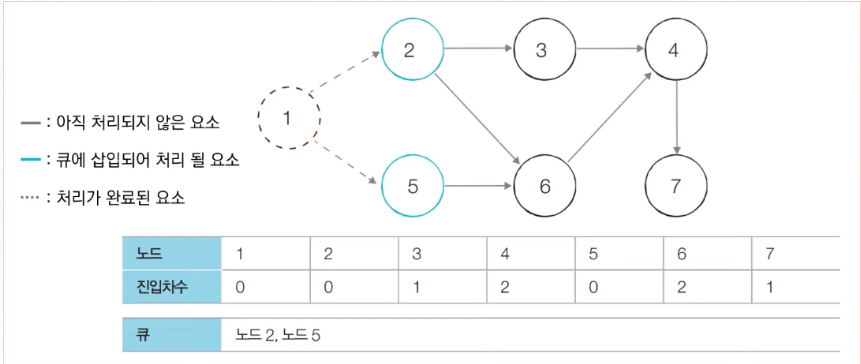
- 큐에서 노드 1을 꺼낸 뒤에 노드 1에서 나가는 간선을 제거한다.
- 새롭게 진입차수가 0이 된 노드들을 큐에 삽입한다.
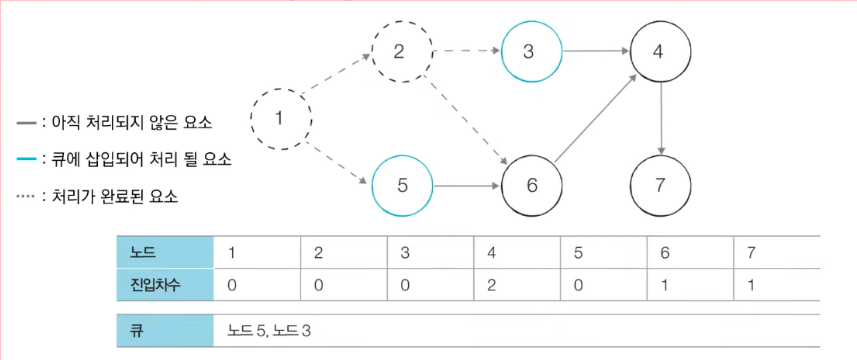
- 큐에서 노드 2를 꺼낸 뒤에 노드 2에서 나가는 간선을 제거한다.
- 새롭게 진입차수가 0이 된 노드들을 큐에 삽입한다.
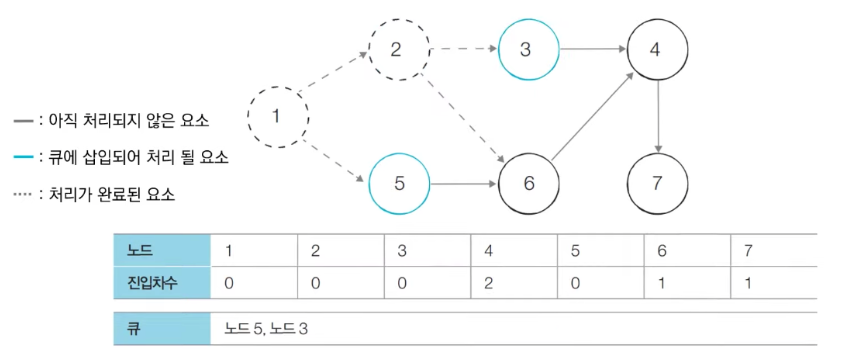
- 큐에서 노드 5를 꺼낸 뒤에 노드 5에서 나가는 간선을 제거한다.
- 새롭게 진입차수가 0이 된 노드들을 큐에 삽입한다.
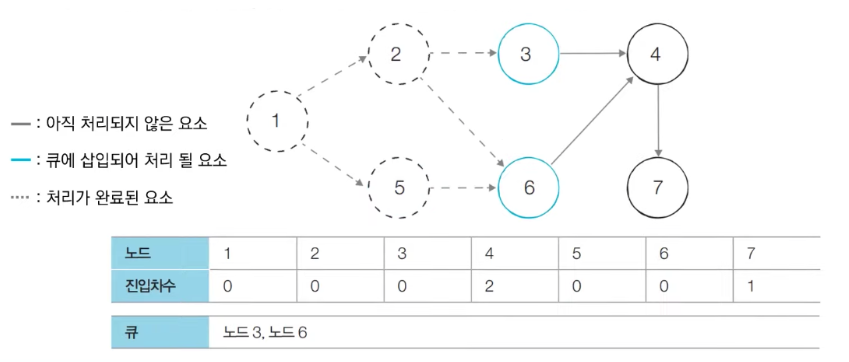
- 큐에서 노드 3를 꺼낸 뒤에 노드 3에서 나가는 간선을 제거한다.
- 새롭게 진입차수가 0이 된 노드들을 큐에 삽입한다.
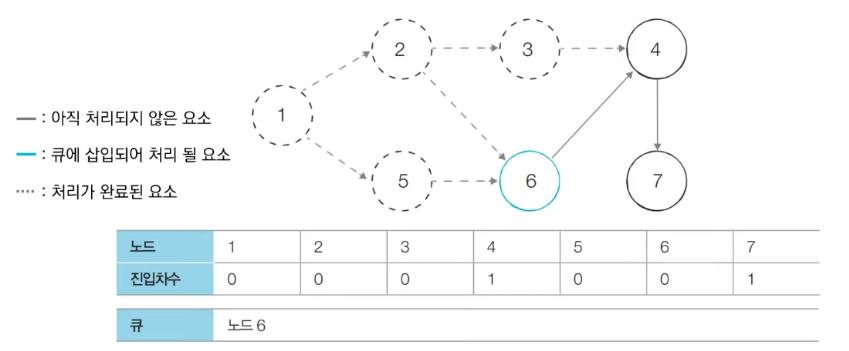
- 큐에서 노드 6를 꺼낸 뒤에 노드 6에서 나가는 간선을 제거한다.
- 새롭게 진입차수가 0이 된 노드들을 큐에 삽입한다.
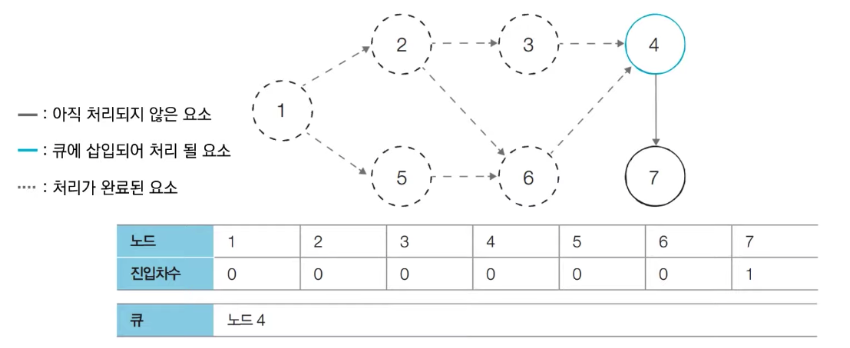
- 큐에서 노드 4를 꺼낸 뒤에 노드 4에서 나가는 간선을 제거한다.
- 새롭게 진입차수가 0이 된 노드들을 큐에 삽입한다.
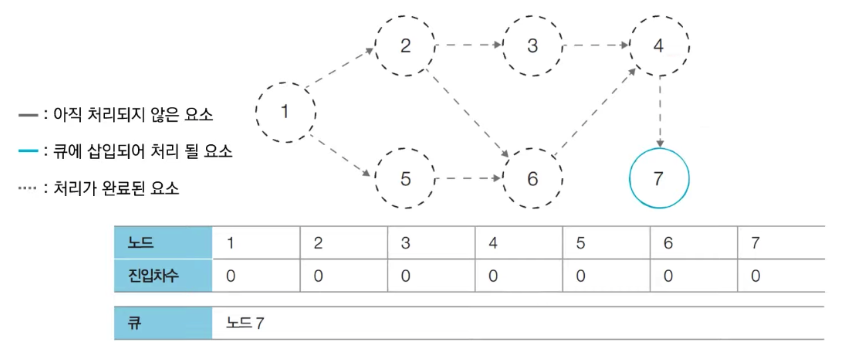
- 큐에서 노드 7를 꺼낸 뒤에 노드 7에서 나가는 간선을 제거한다.
- 새롭게 진입차수가 0이 된 노드들을 큐에 삽입한다.
큐에 삽입된 전체 노드 순서: 1 -> 2 -> 5 -> 3 -> 6 -> 4 -> 7
스택으로 구현시, 방식은 같지만 결과가 다르게 나온다.
큐를 사용한 위상 정렬 코드
import sys
from collections import deque
input = sys.stdin.readline
v, e = map(int, input().split()) # 노드의 갯수와 간선의 갯수를 입력 받기
inDegree = [0] * (v+1) # 모든 노드에 대한 진입 차수는 0으로 초기화
graph = [[] for _ in range(v+1)] # 각 노드에 연결된 간선 정보를 달기 위한 연결 리스트 초기화
# 방향 그래프의 모든 간선 정보를 입력 받기
for i in range(e):
a, b = map(int, input().split())
graph[a].append(b) # 노드 A에서 B로 이동 가능
inDegree[b] += 1 # 진입 차수를 1 증가
# 위상 정렬 함수
def TopologySort():
result = [] # 알고리즘 수행 결과를 담을 리스트
queue = deque() # 큐 기능을 위한 deque 라이브러리 사용
for i in range(1, v+1): # 첫 시작때 진입 차수가 0인 노드를 큐에 삽입
if inDegree[i] == 0:
queue.append(i)
while queue: # 큐가 빌 때까지 반복
current = queue.popleft() # 큐에서 원소 꺼내기
result.append(current)
for i in graph[current]: # 해당 원소와 연결된 노드들의 진입 차수 1 빼기
inDegree[i] -= 1
if inDegree[i] == 0: # 새롭게 진입 차수가 0이 되는 노드를 큐에 삽입
queue.append(i)
for i in result:
print(i, end='')
TopologySort()3. 인접 행렬, 인접 리스트 형태의 그래프 위상 정렬
인접 행렬
from collections import deque
adj_mat = [[0, 0, 1, 1, 0, 0],
[0, 0, 0, 1, 1, 0],
[0, 0, 0, 1, 0, 1],
[0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 1],
[0, 0, 0, 0, 0, 0]]
def TopologicalSort(matrix):
inDegree = []
que = deque()
answer = []
for i in range(len(matrix)):
temp = 0
for j in range(len(matrix)):
temp += matrix[j][i]
inDegree.append(temp)
for i in range(len(inDegree)):
if inDegree[i] == 0:
que.append(i)
while que:
node = que.popleft()
answer.append(node)
for i in range(len(matrix[node])):
if matrix[node][i] != 0:
inDegree[i] -= 1
if inDegree[i] == 0:
que.append(i)
return answer
print(TopologicalSort(adj_mat)) 인접 리스트
import queue
adj_list = {0:[2, 3], 1:[3, 4], 2:[3, 5], 3:[5], 4:[5], 5:[]}
def TopologicalSort(list):
myQue = queue.Queue()
inDegree = [0] * len(list)
answer = []
for i in range(len(list)):
for j in range(len(list)):
temp = list[j]
for k in range(len(temp)):
if temp[k] == i:
inDegree[i] += 1
for i in range(len(inDegree)):
if inDegree[i] == 0:
myQue.put(i)
while not myQue.empty():
node = myQue.get()
answer.append(node)
for i in range(len(list[node])):
idx = list[node][i]
inDegree[idx] -= 1
if inDegree[idx] == 0:
myQue.put(idx)
return answer
print(TopologicalSort(adj_list))