참조: https://www.youtube.com/watch?v=GtqHli8HIqk
참조: https://galid1.tistory.com/507
1. Dynamic Programming이란
먼저, Optimization Problem(최적화 문제)에 대해 알아보자
Optimization Problem(최적화 문제)
- 문제를 해결하는 최적의 답(Optimal Solution)을 찾아야 하는 문제
- Optimal Solution은 하나 이상일 수 있다.
- Maximum 혹은 Minimum Value를 가지는 Solution을 찾는 문제들이 주를 이룬다.
ex
1. 가장 빨리 도착하는 경로의 소요 시간은?
-> 여기서 소요 시간은 Value이며, 경로 자체는 Solution이 된다
2. 언제 주식을 사고 팔 때 가장 수익이 높은지?
-> 마찬가지로, 주식을 사고 팔 때 자체가 Solution이 되며 수익이 Value가 된다.
Dynamic Programming(DP)
- 이러한 Optimization Problem을 해결하는 전략 중 하나
- Subproblem(s)의 Optimal Solution(s)를 활용해서 문제의 최적의 해를 찾는 방식
- 겹치는(Overlapping) Subproblem은 한번만 계산하고, 그 결과를 저장한 뒤 재사용한다.
2. Dynamic Programming 접근 방식

Top-Down 방식
- Divide and Conquer와 비슷하지만 DP의 경우 작은 부분의 문제의 답이 항상 같아야한다.
- 재귀함수로 구현하여 큰 문제를 진입하여 만약 풀리지 않는다면, 작은 문제부터 풀어나가는 식이다.
- Memoization: Function Call 결과를 저장해서 이 후에 같은 input에 대한 호출은 저장한 결과를 사용하는 것
Bottom-Up 방식
- for loop를 돌며 작은 문제부터 차근차근 구해나아가는 방법.
3. DP를 사용한 알고리즘 설계 순서
- 순서는 다음과 같다.
1. 주어진 문제의 Optimal Solution이 구조적으로 어떤 특징을 가지는 지 분석한다.
2. 재귀적인 형태로 Optimal Solution의 value를 정의한다.
3. 위의 주어진 방식으로 Optimal Solution의 value를 구한다.
4. 지금까지 계산된 정보를 바탕으로 Optimal Solution을 구한다.
4. DP를 활용한 예제 문제
Climbing Stairs

Top-Down 방식
- 주어진 문제를 subproblem들로 나눈다.
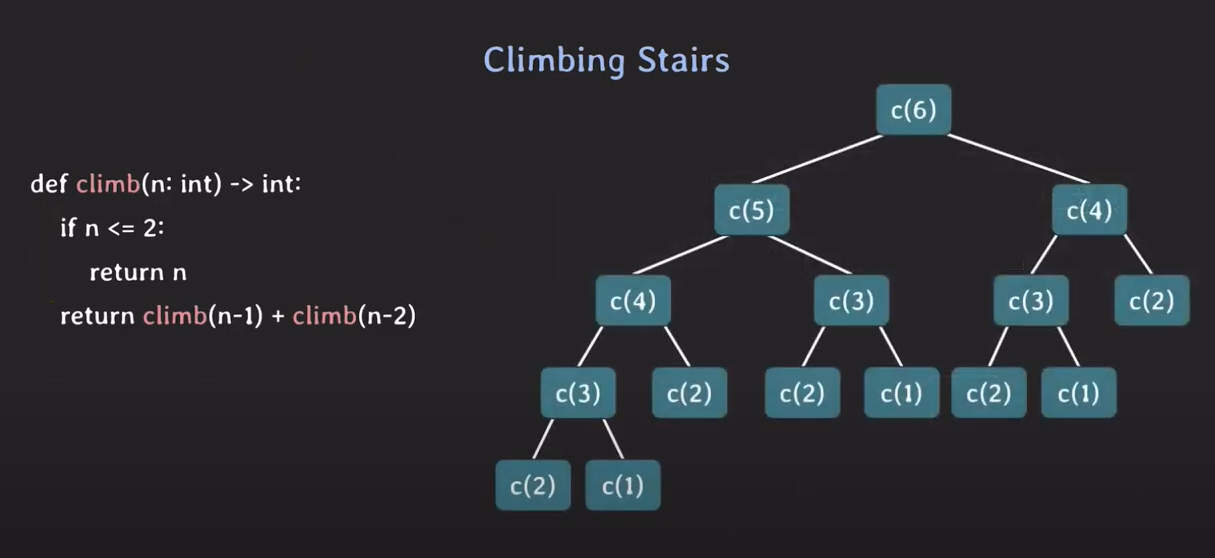
- 이렇게 재귀적으로 나누고, n값에 6을 호출한다면 오른쪽 표와 같이 중복된 값들이 나오게 된다.
- 이렇게 겹치는(Overlapping) Subproblem은 처음 한번만 계산하고, 결과를 메모해 뒀다가 이 후에 재사용하는 방식으로 설계한다.
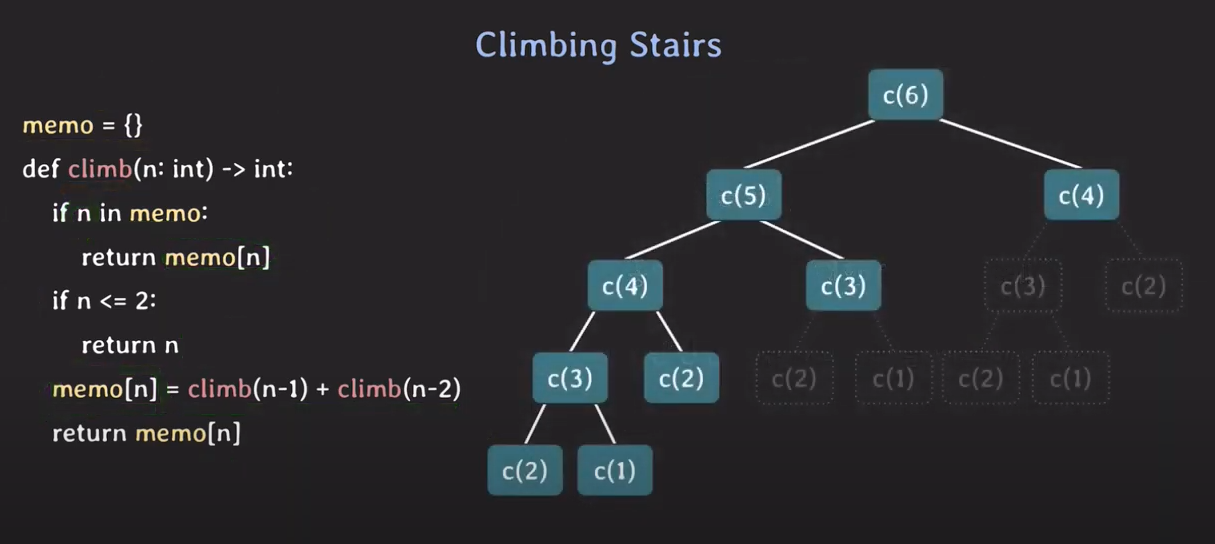
- 이렇게 설계한다면, 중복되는 c(1), c(2), c(3), c(4)를 재사용하게 된다.
Bottom-Up 방식

5. 예제의 시간 복잡도

