참조: https://velog.io/@cyranocoding/%EB%8F%99%EC%A0%81-%EA%B3%84%ED%9A%8D%EB%B2%95Dynamic-Programming%EA%B3%BC-%ED%83%90%EC%9A%95%EB%B2%95Greedy-Algorithm-3yjyoohia5
참조: https://www.youtube.com/watch?v=_IZuE7NIeW4&t=151
Greedy Algorithm(탐욕법)이란
- 문제를 해결하는 과정에서 그 순간순간마다 최적이라고 생각되는 결정하는 방식으로 진행한다.
즉, 미래를 고려하지 않고 오직 현재 시점에 가장 좋은 선택을 하며 최종 해답에 도달하는 문제 해결 방식이다.
가장 숫자가 큰 요소 찾기
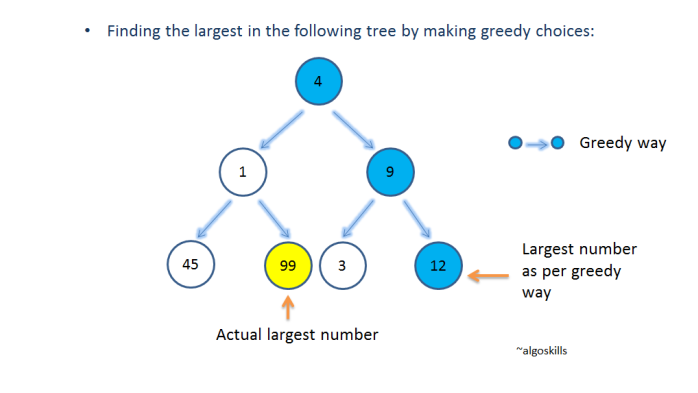
해당 예시에서 가장 큰 수는 99이지만, 그리디 알고리즘을 사용한다면, 4 -> 9 -> 12 순으로 현재 시점에 가장 좋은 선택을 하며 진행을 하고, 결국 12라는 결과가 나오게 된다.
이처럼 그리디 알고리즘은 항상 최적의 해의 결과가 나오지 않지만 가장 큰 장점은 계산 속도가 매우 빠르다는 점이다.
Greedy Algorithm(탐욕법) 사용 조건
- 탐욕스런 선택 조건(Greedy Choice Property)
: 탐욕적인 선택은 항상 안전하다는 것이 보장되어야 한다. 즉, 현재의 선택이 미래에 선택에 영향을 주지 않는 조건
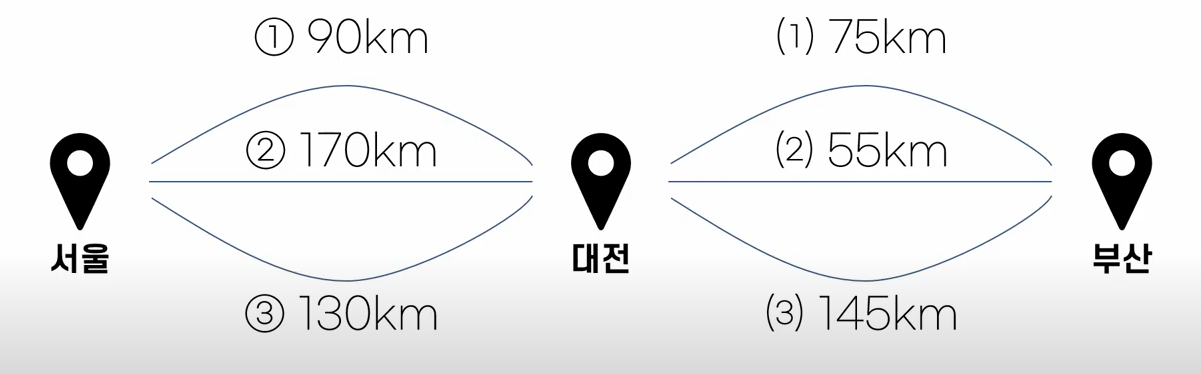
서울에서 부산까지 최소 경로로 이동하는 해답을 찾고 있을때, 서울에서 대전까지 경로를 선택하는 것이 대전에서 부산까지 경로를 선택하는 것에 영향을 미치지 않으니 현재 서울에서 대전까지 가는 최소 경로를 선택하면 된다.
- 최적 부분 구조 조건(Optimal Substructure)
: 문제에 대한 최종 해결 방법이 부분 문제에 대해서도 또한 최적의 해결 방법이다. 즉, 부분의 최적 해가 모이면 전체의 최적 해가 된다.
위의 예시에서 서울에서 부산까지 가는 경로를 구할때, 서울에서 대전까지 가는 경로 구하기와 대전에서 부산까지 가는 경로구하기로 나눌 수 있다.
핵심은 어떻게 정렬해야 이 두 가지 조건을 만족할지, 어떻게 정렬해야 미래에 선택을 따지지 않고 현재만 고려해도 최적 해를 구할 수 있을까를 생각해야한다.
예제
백준 예제 11047문제
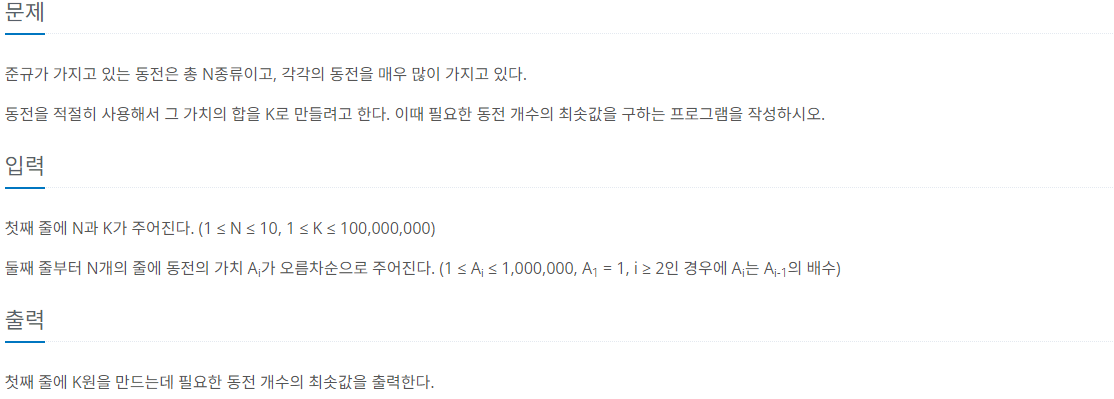
- 가장 대표적인 탐욕법을 활용한 문제이다.
- 입력 조건의 경우 동전의 가치가 전 동전의 배수 만큼 들어온다.
- 동전 입력은 오름차순으로 입력된다.
동전 개수의 최솟값을 출력하는 문제이니 가장 큰 동전부터 나눠 몫을 카운트 해주며 받은 돈이 0이 될 때까지 진행한다.
import sys
input = sys.stdin.readline
N, total = map(int, input().split())
coins = []
for _ in range(N):
coins.append(int(input()))
result = 0
def Exchange():
global result
global total
for i in range(N-1, -1, -1):
if total <= 0:
break
result += total // coins[i]
total = total % coins[i]
Exchange()
print(result)