[C++] 백준 2437번: 저울

문제 출처

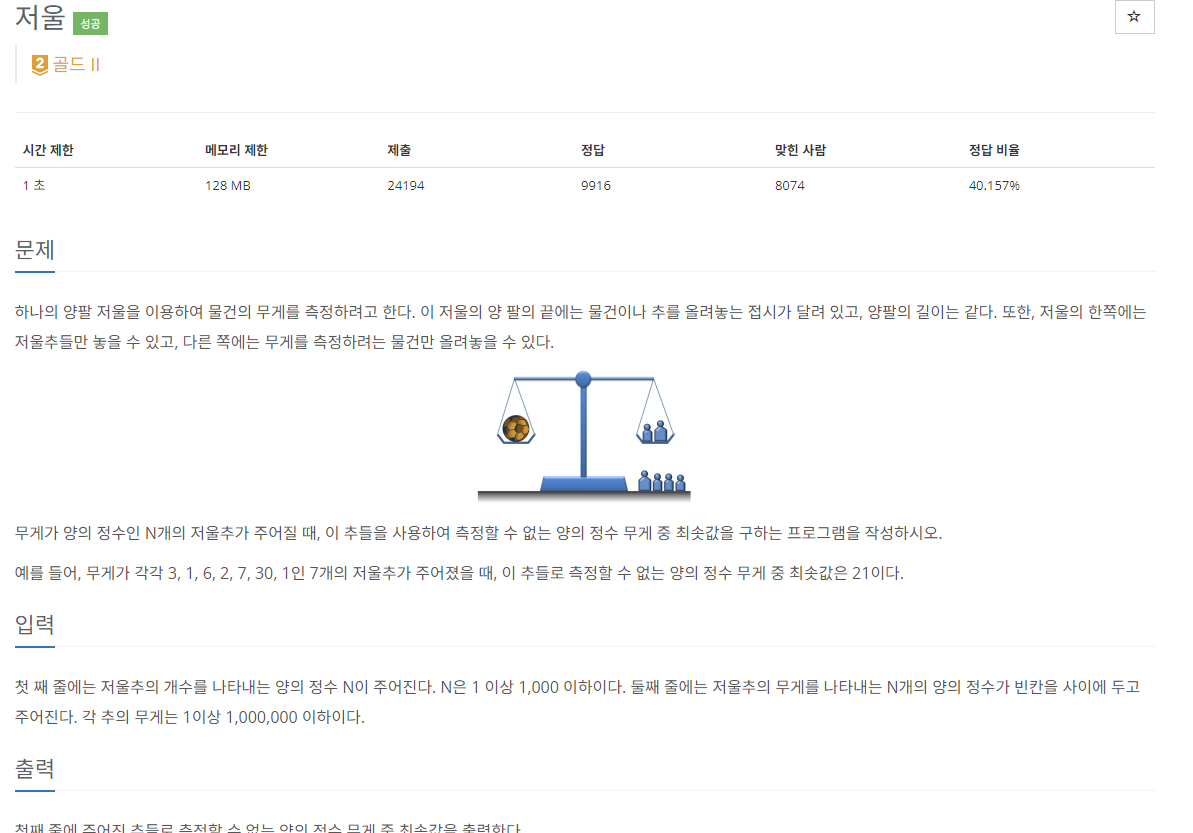
오랜만에 되게 재밌는 문제를 만났다. 처음엔 DP를 생각하였지만 1,000,000 * 1000이 이미 십억이기에 일반적인 DP로는 풀 수 없겠다. 생각하고 변형DP를 찾아보았지만 그마저도 쉽지 않았다. 그러다 예시에 나와있는 숫자들을 하나씩 써보니 해답이 나왔다.

풀이

풀이는 다음과 같은 두 가지 사전 작업으로 이뤄진다.

1. 우선 추들이 무게 순으로 정렬이 되어있다.
2. i번째 추까지 도달하였다는 것은 그 앞에것들은 이미 1부터 k수까지 연속이다.

2번이 이해하기 좀 어려운데 예시를 살펴보면

무게가 1 1 2 5인 총 4개의 추가 있다.
index = 0 일때 1이고 index가 2일때 1,2를 나타낼수 있다. index가 3일때 1,2 에 +2를 해서 1,2,3,4까지 만들 수 있다. 눈치빠르면 다음과 같이 생각할 수 있다. 마지막 가장큰 수만 저장해놓으면 되겠구나. 여기서 index 4가 되면 무게가 5인 추가있다. 따라서 1,2,3,4,5,6,7,8,9까지 만들수 있다. 가장큰 수인 4만 저장해두었다가 5와 더하면된다. 만약 이때 다음 index 에 해당하는 추의 무게가 11이상이라면 10이 답이된다. 결국 핵심은 가장 큰 수를 계속 저장해두는 것이다.

전체 풀이는 다음과 같다.

#include<iostream>
#include<vector>
#include<algorithm>
#include<queue>
#include<tuple>
#include<map>
#include<stack>
#include<set>

using namespace std;

int N;
vector<int> arr;

int main()
{
	ios_base::sync_with_stdio(false); cin.tie(NULL); cout.tie(NULL);
	cin >> N;
	
	arr.resize(N);
	
	for ( int i = 0; i < N; i++ )
	{
		cin >> arr[i];
	}
	sort(arr.begin(), arr.end());
	if ( arr[0] != 1 )
	{
		cout << 1 << endl;
		return 0;
	}
	int max_num = arr[0];
	for ( int i = 1; i < N; i++ )
	{
		if ( arr[i] - 1 <= max_num )
		{
			max_num += arr[i];
		}
		else
		{
			cout << max_num + 1 << endl;
			return 0;
		}
	}

	cout << max_num + 1 << endl;

	return 0;
}