[11049] 행렬 곱셈 순서

Benjamin·2023년 4월 30일

BAEKJOON

목록 보기

61/70

💁‍♀️ dp이용!

이 문제는 dp로 접근하는것을 몰랐으면 못풀었을것같고, 또 dp인걸 알고있음에도 점화식을 어떻게 세워야할지 감이오지않았던 문제이다.

📌점화식을 구하기 막막할 때는 동적 계획법의 특징을 다시 한 번 떠올려보자!
📌부분 문제를 구해 큰 문제를 해결하는 방식이 중요하다!!
📌따라서 부분 문제가 해결됐다고 가정하고, 점화식을 떠올려 보는것도 점화식을 세울 수 있는 좋은 방법 중 하나이다.

문제 분석

1~N개를 모두 곱했을 때 최소 연산 횟수를 구하는 문제이다.
만약 전체 N개가 아닌부분 영역, 예를 들면 1~N-1, 2~N, 3 ~ N-2 등 전체 N을 제외한 모든 부분 구역을 1개의 행렬로 만드는 데 필요한 최소 연산 횟수를 알고 있다고 가정해보자.

어떻게 최소 연산 횟수를 구할 수 있을까?
점화식을 정의해보자.

D[i][j] : i~j 구간의 행렬을 합치는 데 드는 최소 연산 횟수

다음과 같이 N번째 행렬을 제외한 모든 행렬이 합쳐진 경우를 떠올려보자.

D[1][N-1],D[N][N]을 안다고 가정했으므로 1개의 행렬로 합치는 데 드는 횟수는 다음과 같다.

D[1][N-1] + D[N][N] + a
(a = 두 행렬을 합치는 데 드는 값)

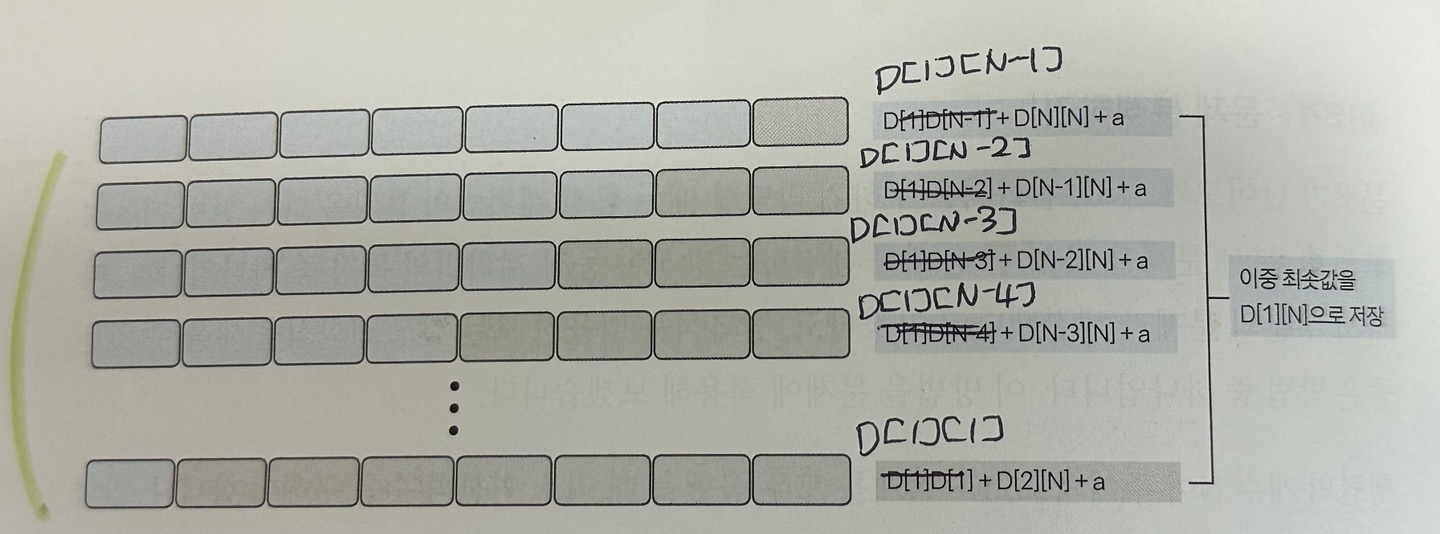
이 아이디어를 바탕으로 생각해보면 최솟값을 찾는 식을 구할 수 있다.

풀이 방법 1

행렬 구간에 행렬이 1개일 때 = 0 리턴
행렬 구간에 행렬이 2개일 때 = 앞 행렬 row 값 뒤 행렬 row 값 뒤 행렬 column값 리턴
행렬 구간에 행렬이 3개 이상일 때 : 다음 조건식의 결괏값 리턴

for(i : 시작행렬 ~종료 행렬) {
	min = Math.min(min, D[s][i] + D[i+1][e] + a(s행렬의 row * i행렬의 row * e행렬의 column))
}

구하려는 영역의 행렬 개수가 3개 이상일 때는 영역을 다시 재귀 형식으로 쪼개면서 계산하면된다.
점화식을 재귀 형태, 즉 톱-다운 방식으로 구현한다.

Troubleshooting

import java.io.IOException;
import java.util.Scanner;
public class Main {
	public static void main(String[] args) throws IOException {
		Scanner sc = new Scanner(System.in);
		int N = sc.nextInt();
		int[][] info = new int[N][2];
		int[][] result = new int[N][4];
		for(int i=0; i<N ;i++) {
			info[i][0] =  sc.nextInt();
			info[i][1] =  sc.nextInt();
		}
		//A정보
		result[0][0] = 0;
		result[0][1] = 0;
		result[0][2] = info[0][0];
		result[0][3] = info[0][1];
		
		//B정보
		result[1][0] = result[0][2]; //A의 행
		result[1][1] = result[0][3]; //A의 열
		result[1][2] = info[1][0]; //B의 행
		result[1][3] = info[1][1]; //B의 열
		
		System.out.println(dp(N, info, result));
	}
	
	public static int dp(int N, int[][] info, int[][] result) {
		int answer = 0;
		for(int i=2; i<N; i++) {
			int cnt = 0;
			int cRow = info[i][0];
			int cColumn = info[i][1];
			int aRow = result[i-1][0];
			int aColumn = result[i-1][1];
			int bRow = result[i-1][2];
			int bColumn = result[i-1][3];
			
			long firstAndSecondMultiple = (aRow * aColumn * bColumn) + (aRow * bColumn * cColumn);
			long secondAndThirdMultiple = (bRow * bColumn * cColumn) + (aRow * aColumn * cColumn);
			
			if(firstAndSecondMultiple < secondAndThirdMultiple) {
				result[i][0] = aRow;
				result[i][1] = bColumn;
				result[i][2] = cRow;
				result[i][3] = cColumn;
				cnt = aRow * aColumn * bColumn;
			} else {
				result[i][0] = aRow;
				result[i][1] = aColumn;
				result[i][2] = bRow;
				result[i][3] = cColumn;
				cnt = bRow * bColumn * cColumn;
			}
			answer += cnt;
		}
		answer += (result[N-1][0] * result[N-1][1] * result[N-1][3]);
		return answer;
	}
}

문제

틀렸습니다

원인

반례를 찾았다.

특정 부분이 원인이라기보다, 이렇게하면 결국 새로운 값을 구할때에는 이전에 구한값을 기준으로 하기때문에 비교의 의미보다 값이 누적되는것같다.

해결

비교하며 최솟값을 찾을 수 있도록 아예 다시 짰다.

제출코드

톱-다운 방식으로 구현

import java.io.IOException;
import java.util.Scanner;
public class Main {
	static int[] N;
	static Matrix[] M;
	static int[][] D;
	public static void main(String[] args) throws IOException {
		Scanner sc = new Scanner(System.in);
		int N = sc.nextInt();
		M = new Matrix[N+1];
		D = new int[N+1][N+1];
		for(int i=0; i<D.length ;i++) {
			for(int j=0; j<D[i].length; j++) {
				D[i][j] = -1;
			}
		}
		for(int i=1; i<=N; i++) {
			int y = sc.nextInt();
			int x = sc.nextInt();
			M[i] = new Matrix(y,x);
		}
		System.out.println(dp(1,N));
	}
	
	public static int dp(int s, int e) {
		int result = Integer.MAX_VALUE;
		if(D[s][e] != -1) {
			return D[s][e];
		}
		if(s==e) {
			return 0;
		}
		if(s+1 == e) {
			return M[s].y *M[s].x *M[e].x;
		}
		for(int i=s; i<e; i++) {
			result = Math.min(result, M[s].y* M[i].x*M[e].x + dp(s,i) + dp(i+1, e));
		}
		return D[s][e] = result;
	}
	
	static class Matrix {
		private int y;
		private int x;
		Matrix(int y, int x) {
			this.y =y;
			this.x =x;
		}
	}
}

풀이 방법 2

예시 : ABCD의 행렬의 최솟값을 구하기 위해서는
A(BCD)
(AB)(CD)
(ABC)D
ABCD
중 최솟값을 구하면 된다. 이때 BCD 값, ABC값들은 ABCD 최솟값을 구하는 과정과 똑같은 과정을 거쳐 답을 구할 수 있다.

DP 그래프는 다음과 같이 구상할 수 있다.

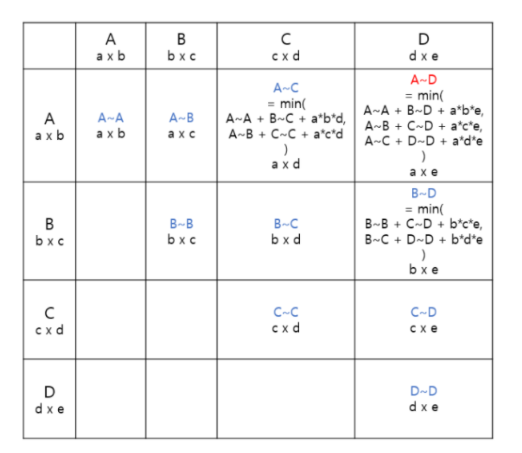
맨 처음에는 모두 0 혹은 문제에서 결과로 불가능한 값을 가지고 있는 dp 이차원 배열 리스트를 만들고, 자기 자신을 곱하는 행렬의 값은 0이다. (자기 자신은 곱하지 않으므로)

위의 그래프를 보면 ABCD (dp[0][4]) 를 구하기 위해서는 BCD, AB,CD ,ABC값이 필요하며 ABC값을 구하기 위해서는 AB와 BC값이 반드시 필요하다.

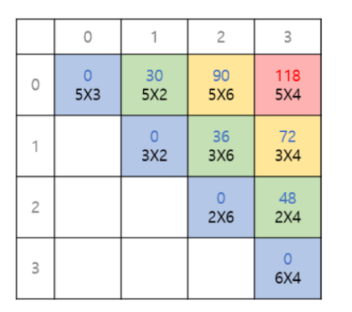
초록 - 주황 - 빨강 순으로 그래프를 채워나가야 한다.

코드

public static void main(String[] args) throws NumberFormatException, IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st;
		int N = Integer.parseInt(br.readLine());
		int[][] dp = new int[N][N];
		int[][] process = new int[N][2];
		for(int i=0; i<N; i++) {
			st = new StringTokenizer(br.readLine());
			process[i][0] = Integer.parseInt(st.nextToken());
			process[i][1] = Integer.parseInt(st.nextToken());
		}
		for(int k=1; k<N; k++) {
			for(int i=0; i+k<N; i++) {
				dp[i][i+k] = Integer.MAX_VALUE;
				for(int j=i; j<i+k; j++)
					dp[i][i+k] = Math.min(dp[i][i+k], dp[i][j]+dp[j+1][i+k] + process[i][0]*process[j][1]*process[i+k][1]);
			}
		}
		System.out.println(dp[0][N-1]);
}

출처
Do it! 알고리즘 코딩 테스트 자바편
https://velog.io/@taurus429/JAVA-%EB%B0%B1%EC%A4%80-11049-%ED%96%89%EB%A0%AC%EA%B3%B1%EC%85%88%EC%88%9C%EC%84%9C
https://velog.io/@turtle601/%EB%B0%B1%EC%A4%80-%ED%96%89%EB%A0%AC-%EA%B3%B1%EC%85%88-%EC%88%9C%EC%84%9C-11049%EB%B2%88