문제분석
최대공약수가 1이라는 이야기는 두 수가 서로소의 관계에 있다는 이야기이다.
n과 서로소 관계에 있는 k의 개수를 구하면 되는 문제이기때문에, 오일러 피를 이용해서 n일때 값을 구하면 된다.
슈도코드
n입력받기
int[] disjoint = new int[n+1];
for(int i=2;i<=n; i++){
if(disjoint[i] == i) {
for(int j=i; j<=n; j = j+i) {
disjoint[j] = disjoint[j] - disjoint[j]/i
}
}
}
disjoint[n] 출력Troubleshooting
import java.util.Scanner;
public class Main {
static int n;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
int[] disjoint = new int[n+1];
for(int i=1 ;i<=n; i++) {
disjoint[i] =i;
}
eulerPhi(disjoint);
System.out.println(disjoint[n]);
}
public static void eulerPhi(int[] disjoint) {
for(int i=2;i<=n; i++){
if(disjoint[i] == i) {
for(int j=i; j<=n; j = j+i) {
disjoint[j] = disjoint[j] - disjoint[j]/i;
}
}
}
}
}문제
백준에서 '런타임에러'가 났다.
원인
A,B의 최대크기가 10^12이기때문에 int타입으로 받을 수 없다.
따라서 long으로 바꿔야하는데, 문제는 여기서 또 발생한다.

빨간 밑줄 오류 : Type mismatch: cannot convert from long to int
배열의 인덱스나 크기에 long타입의 변수를 사용하는 부분은 다 위와같은 오류가 발생하는것이다.
해결
알아보니, array자체가 int크기까지만 가능하도록 디자인되어서 크기(인덱스)를 long으로 할수는 없다고한다.
https://stackoverflow.com/questions/32057664/array-index-property-in-java
-> 이 방법으로는 할 수 없을것같아서, 오일러 피의 다른 공식을 사용하기로 했다.
사용할 방법
Euclidean algorithm을 사용해 풀이할 수 있지만, 최대 10^12의 수들에 대해 계산을 해야하므로 시간제한에 걸린다.
Euler product formula을 사용해 쉽게 풀이할 수 있다.

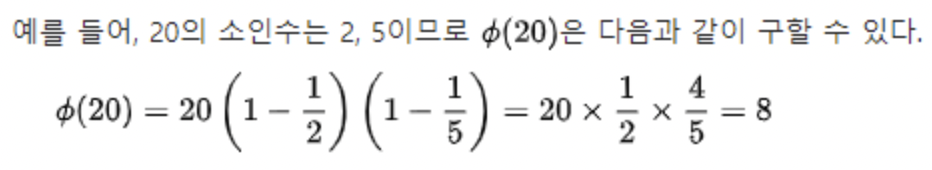
출처 : 위키백과 - 오일러 피 함수
나누어 떨어지는 소인수(p)를 찾아 Euler product formula에 적용시키면 된다.
p-1 / p(= 1- 1/p)를 n에 곱해주어야 한다.
p로 먼저 나눈 후 p-1을 곱해주자.
그런 다음 계속해서 소인수를 찾을지 말지 여부를 결정해주기 위해 n이 p로 나누어 떨어지지 않을 때까지, n/p를 해줃다.
❗️다음과 같은 예외가 있다.
- n이 소수일 때
- n제곱근보다 큰 소인수 중 1인 소인수를 가질 때
Euler product formula을 1회 적용해 두 조건에 대한 euler를 얻을 수 있다.
Troubleshooting 2
import java.util.Scanner;
public class Main {
static long n;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextLong();
long pi = n;
for(int i=2; i*i<=n; i++) {
if(n%i == 0) pi = pi/i*(i-1);
while(n%i == 0) n = n/i;
}
if(n != 1) pi = pi/n*(n-1);
System.out.println(pi);
}
}문제
백준에서 '시간초과'가 났다.
원인
for문에서 i*i<=n;까지 돌도록 조건문을 쓴게 문제였다.
해결
i*i<=n; -> Math.sqrt(n) 으로 수정했다.
sqrt()쓰는것보다 곱셈을하고, n이랑 비교연산을하는게 더 오래걸리는구나.
그리고 이런 작은것에도 시간초과가 날 수 있구나.
제출코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
public class Main {
static long n;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Long.parseLong(br.readLine());
long pi = n;
for(int i=2; i<= Math.sqrt(n); i++) {
if(n%i == 0) pi = pi/i*(i-1);
while(n%i == 0) n = n/i;
}
if(n != 1) pi = pi/n*(n-1);
System.out.println(pi);
}
}아주아주 헷갈렸던 사항
-
for문을 돌 때,
if(n%i == 0)이면 오일러 곱 공식을 쓰는데, 이때 적용되는 i가 어떻게 무조건 소수가 되는건지 처음에 이해가 안됐다.
-> 처음에 2부터 시작하며, 배수는n = n/i;이 식을 통해 가능한 경우가 지워지므로 이후에 오일러 곱 공식에는 무조건 어떤 수의 배수가 아닌 소수만 적용된다! -
마지막에 if문으로 n이 1인지 검사해서, 크다면 오일러 곱 공식을 한 번 더 적용하는데, 이건 n제곱근보다 큰 소인수가 한 개일거라는것이 당연하다고 생각하고 코드를 짜는데, 어떻게 한 개로 보장되는지 이해되지않았다.
에라토스테네스의 체는 왜 n제곱근까지 검사해도 될까?
에라토스테네스의 체를 이용해서 1~n중 소수를 구할 때, n제곱근까지만 검사한다.
n=ab 일때, a가 n제곱근보다 작아지면, b는 n제곱근보다 커지는데 이때 b의 경우는 2가지가 있다.
//
1. n제곱근보다 큰 b가 소수일 때
2. n제곱근보다 큰 b가 소수가 아닐때
//
1번의 경우는 소수이므로, 건드지 않는게 맞다.
2번의 경우는 'b = cd' 이런식으로 표현될 수 있는데, c가 b제곱근보다 작고, d가 b제곱근보다 크면, 'n제곱근 > b제곱근'이므로 'n제곱근 > c'라서 b의 인수인 c로 b가 진작에 나눠지므로 b를 삭제했을것이다.
따라서 에라토스테네스의 체는 n제곱근까지만 검사하면 된다.
n=a*b 일때, a가 n제곱근보다 작아지면, b는 n제곱근보다 커지는것을 생각해보자.
n제곱근이 반으로 나누는 것이기때문에, 이것보다 큰 수 2개를 곱하면 무조건 n보다 커진다.
따라서 n제곱근보다 큰 소인수가 있다면, 그것은 무조건 한 개 일것이다.
- for문 안에서 for문 조건에 쓰이는 기준변수가 업데이트되면, 그 다음 반복부터는 업데이트 된 변수로 적용될까?
for(int i=2; i*i<=n; i++) {
if(n%i == 0) pi = pi/i*(i-1);
while(n%i == 0) n = n/i;
}답은 yes!
-> 아니 그러면, 계속해서 업데이트 된 n제곱근까지만 for문을 도는데, 이렇게 업데이트 된 기준으로 돌아도 for문을 끝내고나서 소인수가 남는경우에는 그게 한 개라는게 어떻게 증명되지?
