🙋🏻♀️에라토스테네스의 체 이용!
문제분석
A이상 B이하의 거의 소수 개수를 출력하는 문제다.
에라토스테네스의 체를 이용해 B의 제곱근까지 소수를 구하고, 제곱했을 떄 A이상 B이하인 수의 개수를 출력하면 될 것 같다.
에라토스테네스의 체를 이용하니, 시간제한 2초안에 가능할 것으로 판단된다.
슈도코드
A B 입력받기
int[] number = new int[B+1]
primeNumber(number)
int count=0;
for(int i = Math.sqrt(A); i<= Math.sqet(B); i++) {
number의 값이 0이면 count++
}
count 출력
public static void primeNumber(int[] number) {
for(int i=2; i<Math.sqrt(B); i++){
for(int j=2*i; j<=B; j = j+i) {
if(값이 0이먄) {
continue
}
해당 값 0으로 만들기
}
}
}Troubleshooting
import java.util.Scanner;
public class Main {
static int A, B;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
A = sc.nextInt();
B = sc.nextInt();
int[] number = new int[B+1];
int count=0;
primeNumber(number);
for(int i = (int)Math.sqrt(A); i<= Math.sqrt(B); i++) {
if(number[i]==0) count++;
}
System.out.println(count);
}
public static void primeNumber(int[] number) {
for(int i=2; i<Math.sqrt(B); i++){
for(int j=2*i; j<=B; j = j+i) {
if(number[j] == 0) {
continue;
}
number[j] =0;
}
}
}
}문제

예제1에서는 답이 25인데, 31이 출력됐다.
원인
- main에서 for문에
int i = (int)Math.sqrt(A)부터 시작하는데, (int)Math.sqrt(A) == 1 이면, 1도 count++ 된다. 하지만 1은 소수가 아니므로 제외해야한다. - 또한 (int)Math.sqrt(A) 부터 탐색하면 안된다. double형으로 소수점까지 나올 수 있기때문에 강제로 int형변환하면 버림되는데, 버림하는게아니라 올림을 해야한다.
- number배열을 인덱스와 같은 값으로 초기화하지않았다.
해결
- i == 1이면 continue되도록했다.
- Math.ceil()을 써서 올림했다.
- for문을 사용해 인덱스와 동일한 값으로 초기화했다.
Troubleshooting 2
문제
여전히 예제의 결과가 답과 다르게 나온다.
원인
N제곱에서 N이 무조건 2일것이라고 잘못생각했다.
해결
3제곱, 4제곱... 도 표현할 수 있게 로그 밑변환공식을 사용했다.
제출코드
import java.util.Scanner;
public class Main {
static long A, B;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
A = sc.nextLong();
B = sc.nextLong();
int[] number = new int[(int)Math.ceil(Math.sqrt(B))+1];
long count=0;
for(int i=2; i<=number.length-1; i++) {
number[i]= i;
}
primeNumber(number);
for(int i=2; i <= Math.sqrt(B); i++) {
for(int square=2; square<=Math.log(B)/Math.log(i); square++) {
if(number[i] != 0) {
long num = (long)Math.pow(i,square);
if(num >= A && num <= B) count++;
}
}
}
System.out.println(count);
}
public static void primeNumber(int[] number) {
for(int i=2; i<Math.sqrt(B); i++){
for(int j=2*i; j<=number.length-1; j = j+i) {
if(number[j] == 0) {
continue;
}
number[j] =0;
}
}
}
}공부한 사항
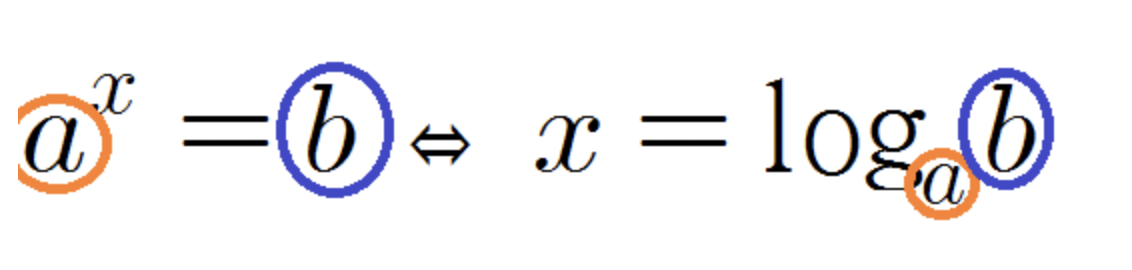
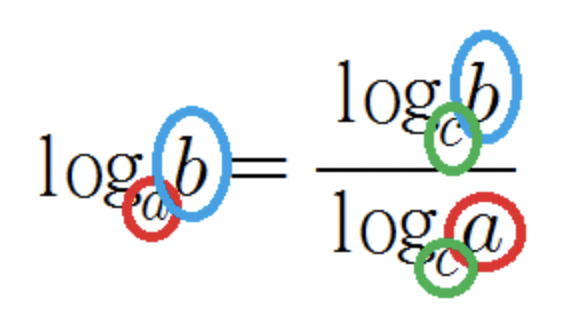
- Math.log(), Math.log10()
- 거듭제곱 : Math.pow(a,n) -> a의 n승
