LCS는 문자열을 이용한 대표적인 동적 계획법 문제입니다.
LCS개념 혹은 풀이접근법을 공부하지않으면 이해하기 어려울 수 있기때문에, 이번시간에 공부해봅시다.
개념
우선, 2개의 문자열이 주어집니다.
이 둘의 공통된 가장 긴 문자열을 찾으면 그게 LCS입니다.
공통된 문자열은 서로 왼쪽에서 오른쪽 순으로 이어져야 하며, 이때 중요한건 한 문자열 내에서 꼭 근접한 문자들을 고르지 않아도 됩니다.
예를 들어 "abc", "abg", "bdf", "aeg", "acefg", .. 등등 은 "abcdefg" 의 부분 문자열입니다.
("gfe" 는 거꾸로 적혔으니까 안됩니다.)
-> 길이가 n인 문자열이 있다면 2^n개의 부분문자열의 경우의 수가 있습니다.
이 문제는 컴퓨터과학 문제중 가장 기본적인 문제면서도 diff 라는 두 파일을 비교하는 프로그램을 만드는데 가장 핵심이 됩니다.
DP의 조건
LCS의 가장 기본적인 솔루션은 주어진 문자열들의 모든 부분문자열들을 만들어보고 그중에서 서로 맞는 가장 긴 부분문자열을 고르면 되는것입니다. 이 솔루션은 완전탐색으로 시간복잡도가 큽니다.
따라서 이를 해결하기위해 DP로 풀 수 있습니다.
일단 이 문제가 왜 동적계획법(DP) 로 풀어야 하는지 알아봅시다.
1. 최적의 서브구조
(아래의 경우가 있다고 가정)
- 주어진 각 문자열의 길이 = m, n
- 배열로 표현한 각 문자열 = X[0..m-1], Y[0..n-1]
- L(X[0..m-1], Y[0..n-1])= 두 문자열 X 와 Y의 LCS 의 길이를 반환하는 함수
아래의 내용은 L(X[0..m-1], Y[0..n-1]) 를 재귀적으로 이용한것과 같습니다.
만약 두 문자열의 마지막 문자가 같다면 (X[m-1] == Y[n-1])
L(X[0..m-1], Y[0..n-1]) = 1 + L(X[0..m-2], Y[0..n-2]) 가 됩니다.
즉, 뒤에서부터 같은 문자를 찾으면, LCS 의 길이를 1 증가시키고 각 문자열을 하나씩 줄인뒤 다시 LCS 를 찾는 재귀형식으로 접근하는 것입니다.
만약 두 문자열의 마지막 문자가 같지 않다면 (X[m-1] != Y[n-1])
L(X[0..m-1], Y[0..n-1]) = MAX ( L(X[0..m-2], Y[0..n-1]), L(X[0..m-1], Y[0..n-2])가 됩니다.
즉, 서로 문자가 같지 않으면 두 문자열중 하나만 다음으로 넘어가고 하나는 그대로 두는 방법을 택합니다.
그래프상에서 왼쪽이나 위 중 큰 값을 선택합니다.
그리고 그 문자열들중에 LCS를 다시 찾아서 가장 '긴' 문자열을 찾습니다. (MAX)
<예제>
1) "AGGTAB" 와 "GXTXAYB" 가 LCS 를 구해야할 두개의 문자열이라고 가정.
마지막 문자 'B' 가 서로 같습니다.
L(X[0..m-1], Y[0..n-1]) = 1 + L(X[0..m-2], Y[0..n-2]) == L(“AGGTAB”, “GXTXAYB”) = 1 + L(“AGGTA”, “GXTXAY”)
재귀적인 상황을 살펴보면, 주 LCS 문제는 서브 LCS 문제의 솔루션을 이용해서 풀릴 수 있다는 점이 '최적의 서브구조' 성질을 만족함을 알 수 있습니다.
2. 중복되는 서브문제들
아래에 작성된 코드는 LCS 문제의 재귀적 해결방법 입니다. 알고리즘 자체는 위에 언급된 공식을 따라 작성했습니다.
# python 을 이용한 LCS 문제 해결을 위한 재귀적 솔루션
def lcs(X, Y, m, n):
if m == 0 or n == 0:
return 0;
elif X[m-1] == Y[n-1]:
return 1 + lcs(X, Y, m-1, n-1);
else:
return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n));이렇게 완전탐색 할 경우 최악의 시간복잡도는 O(2n)입니다.
문자열 X 와 Y 가 하나도 맞는 문자가 없을때 나타나는 경우가 최악의 경우죠.
즉, LCS 의 문자열의 개수는 0 이 되는 상황입니다.
위 프로그램의 실행 중에 부분 문자열 AXYT 과 AYZX 의 부분 재귀 트리는 아래와 같습니다.
lcs("AXYT", "AYZX")
/ \
lcs("AXY", "AYZX") lcs("AXYT", "AYZ")
/ \ / \
lcs("AX", "AYZX") lcs("AXY", "AYZ") lcs("AXY", "AYZ") lcs("AXYT", "AY")위의 부분 재귀 트리를 보시면 lcs("AXY", "AYZ") 가 두번 중복해서 실행되는것을 보실 수 있습니다. 같은 문제를 두번 풀게 만드는거죠.
전체의 재귀 트리를 그린다면 더 많은 서브 문제들이 중복되서 풀리고 또 풀리게 될겁니다.
이런 문제를 해결하기위해 Memozation 또는 tabulation 을 이용한 DP로 풀여야합니다.
아래는 LCS 문제를 풀기위해 tabulation 을 적용한 솔루션 입니다.
풀이 (LCS의 길이)
배열을 쉽게 구분하기 위해 각 문자열의 첫번째 자리 index를 1 로 설정했습니다. (index 0 인 부분은 Φ (빈자리)로 처리)
행의 'G' 부터 보겠습니다. 'G' 와 'A' 는 서로 공통된 부분이 없으므로 LCS 는 없습니다. 그래서 table[1][1] = 0 이 됩니다.
Φ A G G T A B
----------------
Φ | 0 0 0 0 0 0 0
G | 0 0
X |
T |
X |
A |
Y |
B |'G'와 'AG' 는 'G' 라는 LCS 가 있습니다. 그러니까 LCS 의 길이는 1 이므로 table[1][2] = 1 이 됩니다.
이때 이 1의 값은 대각선 방향으로 넘어오는 값입니다. 즉, 아무것도 없는 행의 공백과 열의 'A' 를 나타내는 table[0][1] = 0 에서 + 1 을 하게되면 table[1][2] = 1 이 되는것 입니다.
이것은 위에서 언급한 '양쪽 문자열의 끝이 일치할 경우, L(X[0..m-1], Y[0..n-1]) = 1 + L(X[0..m-2], Y[0..n-2])' 의 공식과 일치합니다.
Φ A G G T A B
----------------
Φ | 0 0 0 0 0 0 0
G | 0 0 1
X |
T |
X |
A |
Y |
B |'G'와 'AGG' 는 역시 'G' 라는 LCS 가 있습니다. 한쪽 문자열이 하나밖에 없으므로 'G'가 다른쪽 문자열에 두개 있다 하더라도 LCS 가 2배가 될 수는 없겠죠? 그러므로 LCS 는 여전히 1 이므로 table[1][3] = 1 이 됩니다.
(한쪽 문자열이 하나밖에 없고, 특정 위치에서 1의 값이 나왔다면 해당 행 또는 열에서는 그 이후의 모든 값이 1이 될 수 밖에없다)
Φ A G G T A B
----------------
Φ | 0 0 0 0 0 0 0
G | 0 0 1 1
X |
T |
X |
A |
Y |
B |쭉 가다가 'T' 에서는 'GXT' 와 'AGGT' 부분에서 LCS 가 'GT' 가 되어 값이 2가 되는 경우를 보입니다. 즉, table[3][4] = table[2][3] + 1 이 됩니다.
Φ A G G T A B
----------------
Φ | 0 0 0 0 0 0 0
G | 0 0 1 1 1 1 1
X | 0 0 1 1 1 1 1
T | 0 0 1 1 2
X |
A |
Y |
B |나머지도 위와 같은 방식으로 전부 채우면 최종 테이블은 다음과 같습니다.
Φ A G G T A B
----------------
Φ | 0 0 0 0 0 0 0
G | 0 0 1 1 1 1 1
X | 0 0 1 1 1 1 1
T | 0 0 1 1 2 2 2
X | 0 0 1 1 2 2 2
A | 0 1 1 1 2 3 3
Y | 0 1 1 1 2 3 3
B | 0 1 1 1 2 3 4결과적으로 LCS 는 'GTAB' 가 되고 값은 table[7][6] = 4 이 됩니다.
이 인덱스의 뜻은 각 문자열의 끝 문자까지 비교하며 얻은 최대 LCS의 값을 의미합니다.
위의 프로그램 실행의 시간 복잡도는 O(mn)입니다.
구현
//java코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class LCS {
static char[] A, B;
static int[][] dp;
static int max = 0;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 각 문자열을 입력 받는다.
String a = br.readLine();
String b = br.readLine();
// 각 문자열의 길이가 다르므로 따로 저장해둔다.
int alength = a.length();
int blength = b.length();
// 각 문자열을 나눠서 저장할 char 배열.
A = new char[alength + 1];
B = new char[blength + 1];
// 각 문자열을 char 배열에 문자 하나씩 옮겨 담는다.
for(int i = 1; i <= alength; i++) {
A[i] = a.charAt(i - 1);
}
for(int i = 1; i <= blength; i++) {
B[i] = b.charAt(i - 1);
}
// 각 문자의 비교가 끝났을 때, 해당 위치에서 가질 수 있는 LCS의 값을 저장할 2차원 dp테이블을 정의한다.
// 첫 행에서도 이전 문자를 참고할 수 있도록 패딩을 준다.
dp = new int[blength + 1][alength + 1];
// B의 모든 문자열을 A문자열과 비교
for(int i = 1; i <= blength; i++) {
for(int j = 1; j <= alength; j++) {
// 만일 두 문자가 같은 경우
if(B[i] == A[j]) {
// 대각선의 값을 참고하여 LCS의 값을 + 1한다.
dp[i][j] = dp[i - 1][j - 1] + 1;
}
// 두 문자가 다른 경우
else {
// 각 문자열의 이전 문자 중 최대 LCS값을 선택.
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
// 최종으로 탐색한 위치에 LCS의 최대 값이 저장되어 있을 것이다.
System.out.println(dp[blength][alength]);
}
}풀이 (LCS의 문자열)
그렇다면 실제 LCS의 문자열을 어떻게 찾을 수 있을까?
완성된 도표를 이용하면 쉽게 찾을 수 있다.
또 다른 완성된 예시를 보자.
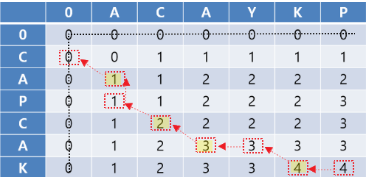
① 마지막 지점 (x, y)에서 부터 출발한다.
② A[x] == B[y] 이면, 대각선 방향으로 좌측상단 이동한다.
③ A[x] != B[y] 이면, 현재 LCS[x-1][y], LCS[x][y-1] 중에서 같은 값이 있는 방향으로 이동
④ x == 0 || y ==0 일 때까지 과정 ①~③을 반복. (LCS[x][y] == 0 인 지점)
⑤ 일치했던 문자를 역순으로 출력한다.
구현
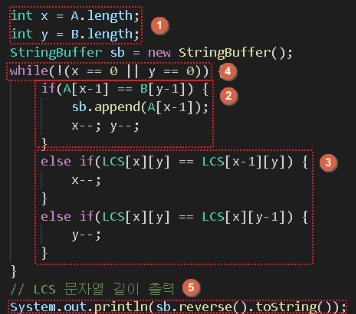
출처
https://www.geeksforgeeks.org/longest-common-subsequence-dp-4/
https://zoosso.tistory.com/187
