TSP
도시들이 있고, 특정 도시에서 도시로 이동할 때 드는 비용이 주어졌을 때 불특정한 도시에서 출발해서 모든 도시를 돌고 다시 출발도시로 돌아왔을 때 드는 최소 비용을 구하는 문제
- 컴퓨터 과학 분야에서 가장 중요하게 취급되는 문제 중 하나
출발도시를 어디로 하느냐?
출발도시를 정해주지 않는데, 사실 어떠한 도시를 출발도시로 하던지 모든 도시를 돌아서 다시 출발도시로 돌아오는데 드는 최소 비용은 같습니다.
다시 출발 도시로 돌아오기 때문에 사이클이 발생하기 때문입니다!
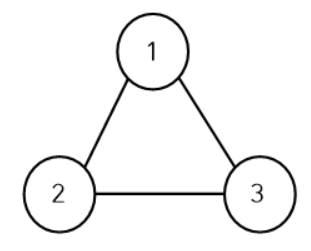
위 예시를 보면, 어디서 출발하든 경로(최소비용)는 동일한것을 알 수 있습니다.
따라서 출발 도시를 어디로 해야할지는 고려할 필요 없이 임의의 도시로 정해두면 됩니다.
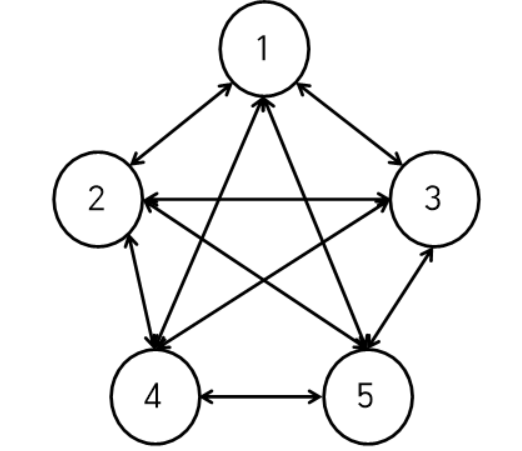
위 그림과 같이 1~5번 도시들과 이동 가능한 경로가 있다고 합시다.(비용 생략)
1번을 출발도시라고 임의로 정하겠습니다.
최소 비용을 구하기 위해서는 깊이 우선 탐색으로 1번 도시부터 방문하지 않은 모든 도시들을 방문하고, 출발 도시까지 도달 했을 때 드는 비용들을 구한 뒤 그 비용들 중 최솟값을 구하면 됩니다.
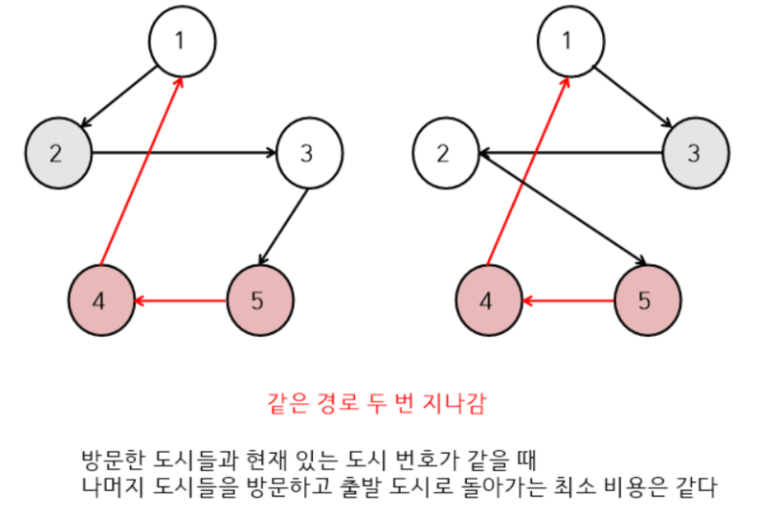
왼쪽 그림 = 1번 도시에서 2번 도시로 갔을 때, 모든 도시를 돌고 출발도시까지 돌아오는 최소 비용의 경로
오른쪽 그림 = 1번 도시에서 3번 도시로 갔을 때, 모든 도시를 돌고 출발도시까지 돌아오는 최소 비용의 경로
그림을 보면 '5->4->1' 의 경로의 최소 비용을 중복해서 구합니다.
이미 방문한 도시들과 현재 위치한 도시가 같은 경우에는 이후 최소 비용이 동일합니다.
따라서 이를 두 번 구하는 것은 효율적이지 않습니다.
도시가 증가함에 따라 이미 구한 최소 비용을 다시 구하는 시간낭비는 기하급수적으로 증가합니다.
이를 방지하기 위해 memoization을 사용합니다. (대표적으로 피보나치 수열을 Top-Down 방식으로 구할 때 사용하는 것이죠.)
최소 비용을 저장하기 위해 2차원 배열을 사용합니다.
행과 열은 최소 비용이 같을 조건. 즉, 이미 방문한 도시들의 집합과 현재 있는 도시 번호입니다.
- d[i][j] = 이미 방문한 도시들의 집합이 i이고 현재 있는 도시가 j일때, 방문하지 않은 나머지 도시들을 모두 방문한 뒤 출발 도시로 돌아올 때 드는 최소 비용.
여기서 i, j의 범위는 도시가 5개 이기 때문에 0<= i < 2^5(32), 0<= j <5 입니다.
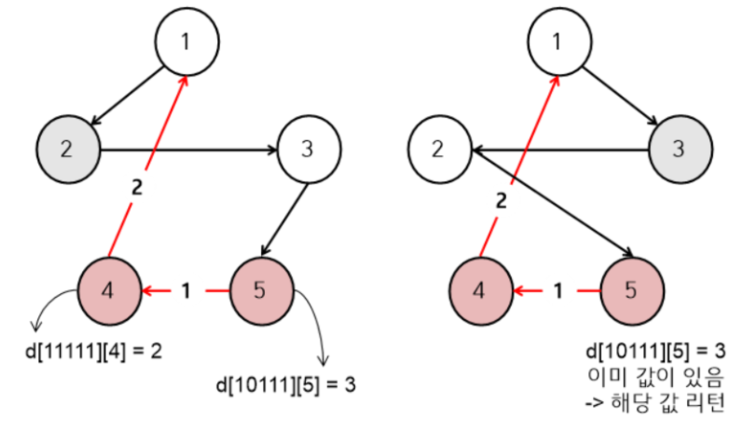
그래서 왼쪽 그림에서 처음에 1->2번 도시를 지났을 때, d[11111][4]와 d[10111][5]를 갱신해주고 (그림에 표시는 안했지만 d[00111][3], d[00011][2]도 갱신 됩니다.)
오른쪽 그림에서 1->3번 도시를 지날 때는 1->3->2->5의 경로를 지나 5번 도시에 도착했을 때 이미 d[10111][5]에 값이 있으므로 더 이상 구할 필요 없이 해당 배열에 있는 값 3을 사용하면 됩니다. (memoization)
이렇게 1번 도시에서 2,3,4,5 번 도시로 이동했을 때 각 도시에서 남은 도시들을 지나 다시 출발 도시로 돌아오는 최소 비용들 중 최소인 값이 우리가 구하고자 하는 값이 됩니다.
이를 재귀함수로 구현하면 최소비용을 구할 수 있습니다.
정리
1) DP를 사용 : 최소 비용 저장위해 2차원 배열 사용
2) 방문한 도시를 나타내기 위해 2진수 비트마스크 활용(코드 상에선 10진수로 사용)
3) 최단경로의 사이클이 만들어지고, 최단 경로는 동일하기 때문에 아무 도시를 시작점으로 해서 경로를 구해도 된다.
대표 문제
비트마스크와 DP를 함께 사용해서 푸는 TSP의 전형적인 문제가 있다.
https://www.acmicpc.net/problem/2098
- DP : 특정 도시들을 방문한 상태일 때 최소 비용을 저장해 놓고 이를 사용
- 비트마스크 : 특정 도시를 방문한 상태를 저장할 때 사용
예를 들어서 1~3번 도시가 있다고 했을 때, 110(2)는 2,3번 도시를 방문한 상태이다.
110(2)를 십진수로 바꿔보면 6(1x22 + 1x21 + 0x20)가 되며, 비트마스크를 통해 우리는 10진수로 사용하면된다.
즉, 이진수로 봤을 때 오른쪽에서 부터 i번째 수가 1이면 i번 도시가 방문, 0이면 i번 도시가 미방문인 상태를 뜻한다.
점화식에 사용한 비트 연산식
모든 도시 순회 판단 연산식
- if( v == (1<<N)-1)
예 ) N=4 (도시의 개수 4) : 1<<4 -1 = 10000(2) -1 = 16-1 = 15 = 1111(2)
각 자리수가 1이기때문에 모든 도시를 방문한 상태라고 판단.
방문 도시 확인 연산식
- if(( v & (1 << i)) == 0)
예 ) i = 3 (3번째 도시 방문 여부 확인) : 1 << 3 = 1000(2) = 8
v&1000(2) 연산 수행 결과가 0이면 해당 도시를 방문하지 않았다고 판단가능 (0000(2) = 0 이 되면 방문x)
& 연산은 두 피연산자가 모두 1이어야 1을 반환하기 때문
방문 도시 저장 연산식
- v | (1<<i)
예) i=2(2번째 도시 저장) : 1<<2 = 100(2)
2번째 자리를 1로 저장하여 방문했다는 사실 표시
