- 위상
어떤 사물이 다른 사물과의 관계 속에서 가지는 위치나 양상
비순환 방향 그래프 (DAG: Directed Acyclic Graph)
Directed Acyclic Graph (DAG)는 사이클이 없는 방향 그래프입니다.
DAG는 이벤트 간의 우선순위를 나타내기 위해 주로 사용됩니다.
위상정렬
- 사이클이 없는 방향 그래프에서 노드 순서를 찾는 알고리즘
- 순서가 정해져있는 작업을 차례대로 수행해야할 때 그 순서를 결정하기위해 사용하는 알고리즘
기능
노드 간의 순서를 결정
특징
- 사이클이 없어야 함
- 항상 유일한 값으로 정렬되지 않음
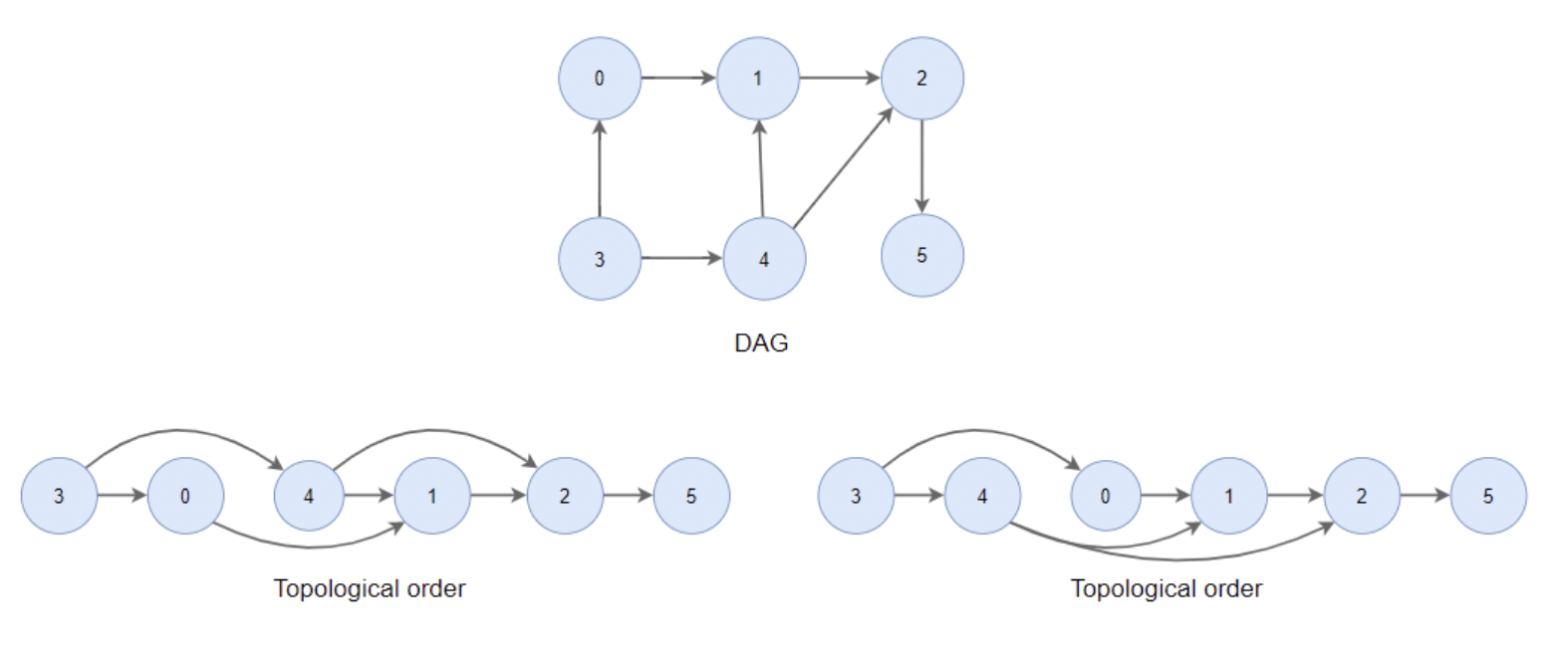
위상 정렬 결과 하나의 DAG에서 하나 이상의 위상 순서(Topological order)가 나올 수 있으며 모든 간선은 오른쪽만 가리키게 됩니다.
예시
- 대학교 선수과목
특정 수강과목에 선수과목이 있다면 그 선수과목부터 수강해야 합니다.
여기서 위상 정렬은 특정 수강과목을 위해 필요한 선수과목의 정렬입니다.
또 다른 예시는 다음과 같습니다.
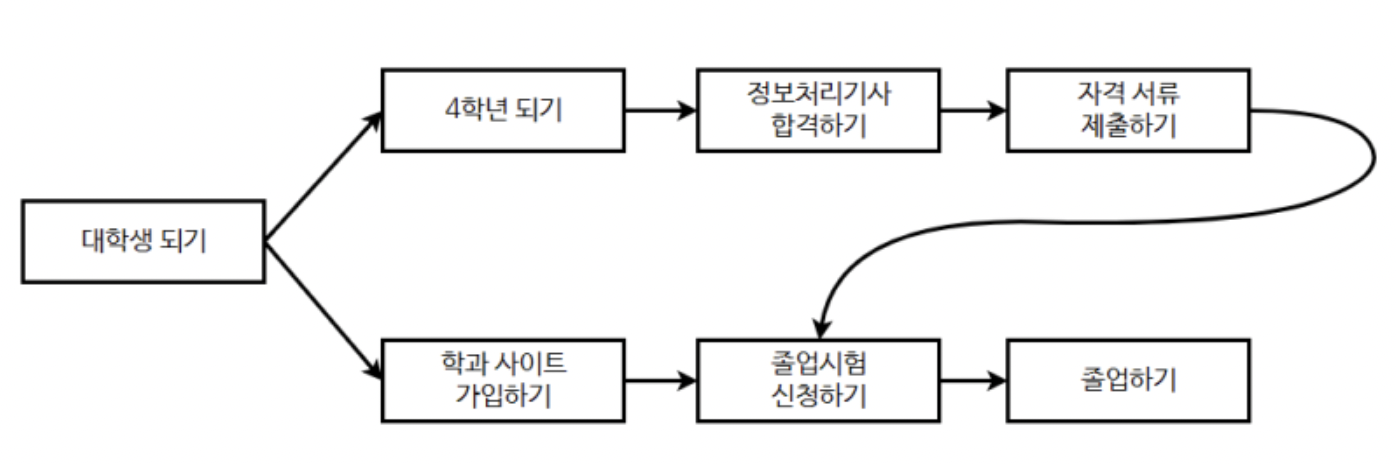
그래프의 흐름은 '조건'으로 해석할 수 있다.
정처기를 취득하기 위해서는 반드시 '4학년 되기'를 만족해야하고, 4학년이 되기 위해서는 그 전에 '대학생 되기'를 만족해야한다.
이렇게 작업의 순서가 정해져 있을 때 작업을 정확하게 정렬해주는 알고리즘이 필요할 수 있다.
위와같이 여러 순서가 정해져있을 때 조건에 부합하는 일직선의 순서를 찾아보자.
- 위상정렬 : 대학생 되기 -> 학과 사이트 가입하기 -> 4학년 되기 -> 정보처리기사 합격하기 -> 자격 서류 제출 하기 -> 졸업시험 신청하기 -> 졸업하기
위와같이 정렬하면 순서대로 작업을 수행했을 때 성공적으로 '졸업하기'까지 갈 수 있다.
위의 답 말고도 다른 답도 존재한다.
위상정렬이 내는 해결책
- 현재 그래프는 위상정렬이 가능한지
- 위상 정렬이 가능하다면 그 결과는 무엇인지
시간 복잡도
O(V+E)
알고리즘
위상정렬을 수행하는 알고리즘에는 크게 2가지가 존재한다.
1. 스택 이용
2. 큐 이용
큐를 이용하는 방법을 소개하겠다.
1. 진입 차수가 0인 정점을 큐에 삽입한다.
2. 큐에서 원소를 꺼내 연결된 모든 간선을 제거한다.
3. 간선 제거 이후 진입 차수가 0이 된 정점을 큐에 삽입한다.
4. 큐가 빌 때까지 2~3번 과정을 반복한다.
모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재하는 것이고, 모든 원소를 방문했다면 큐에서 꺼낸 순서가 위상 정렬의 결과이다.

위와같이 처음에 각 정점과 진입차수 정보를 기입한다.
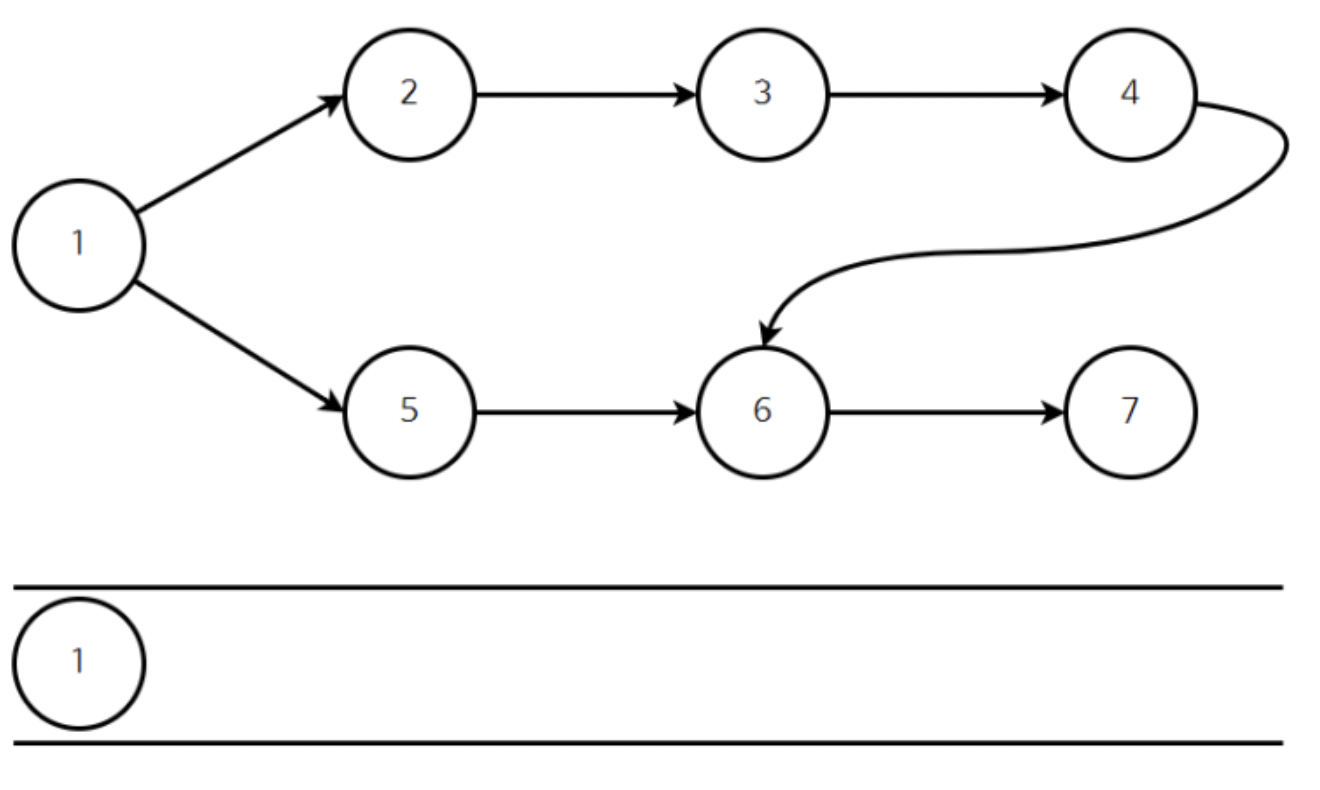
진입차수가 0인 정점 1을 큐에 삽입한다.
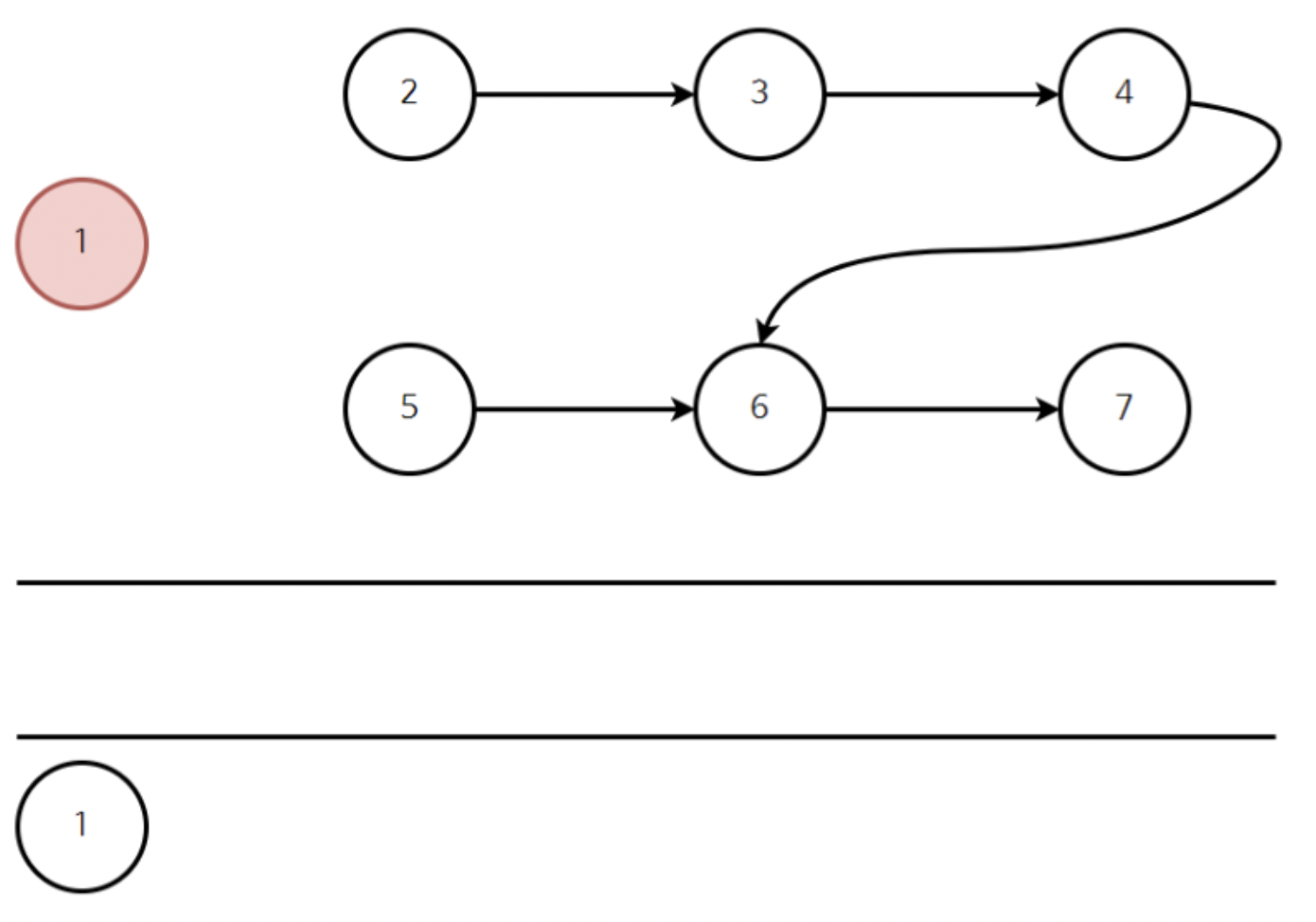
1을 큐에서 꺼낸 뒤 연결되어있던 간선을 다 제거한다. (연결된 노드의 진입차수를 각각 -1한다)
이제 표를 다시 보자.

진입차수가 0인 새로운 정점들을 다시 큐에 삽입한다.
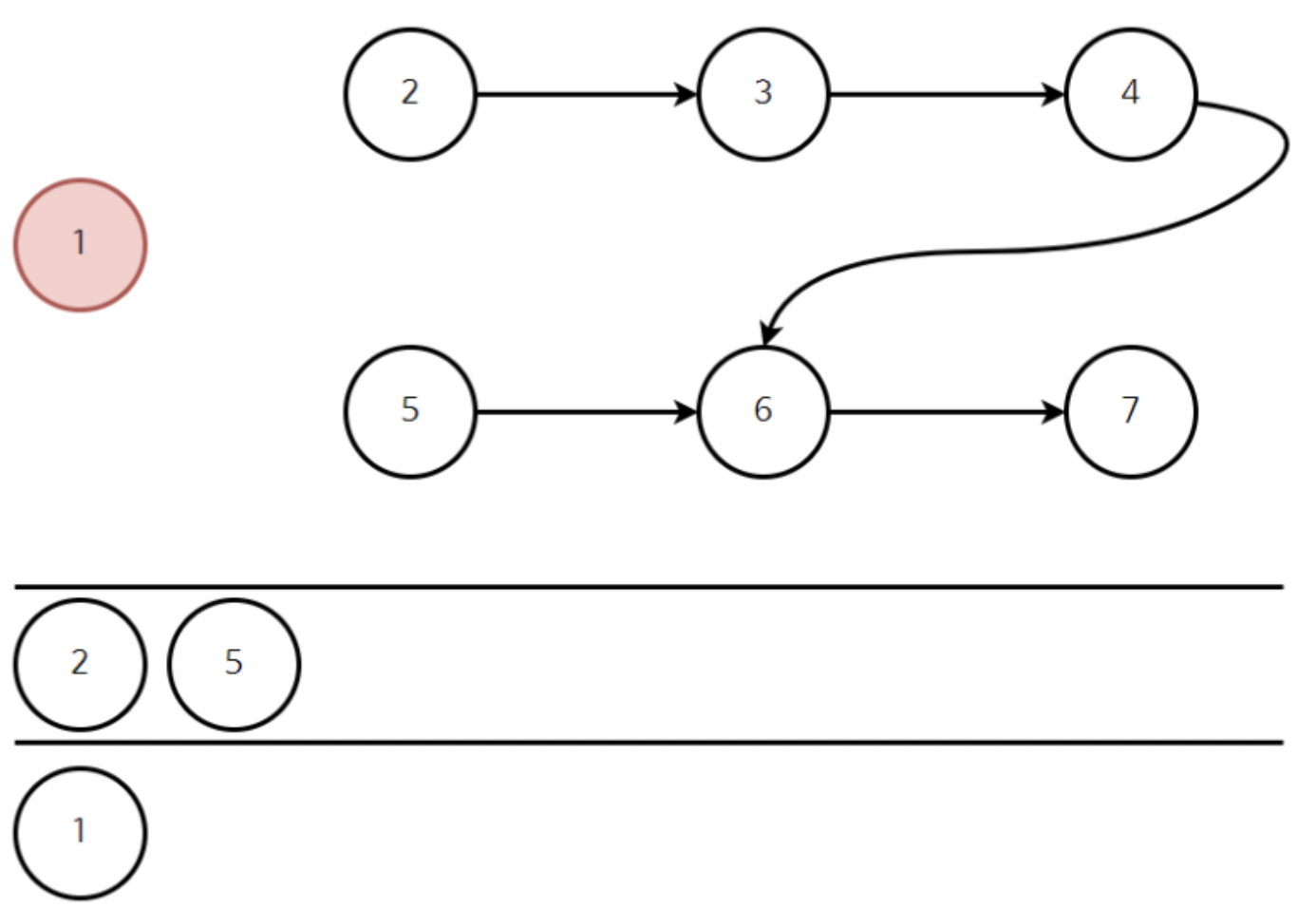
위와 같다. 이제 다시 큐에서 정점 2를 뺴자.
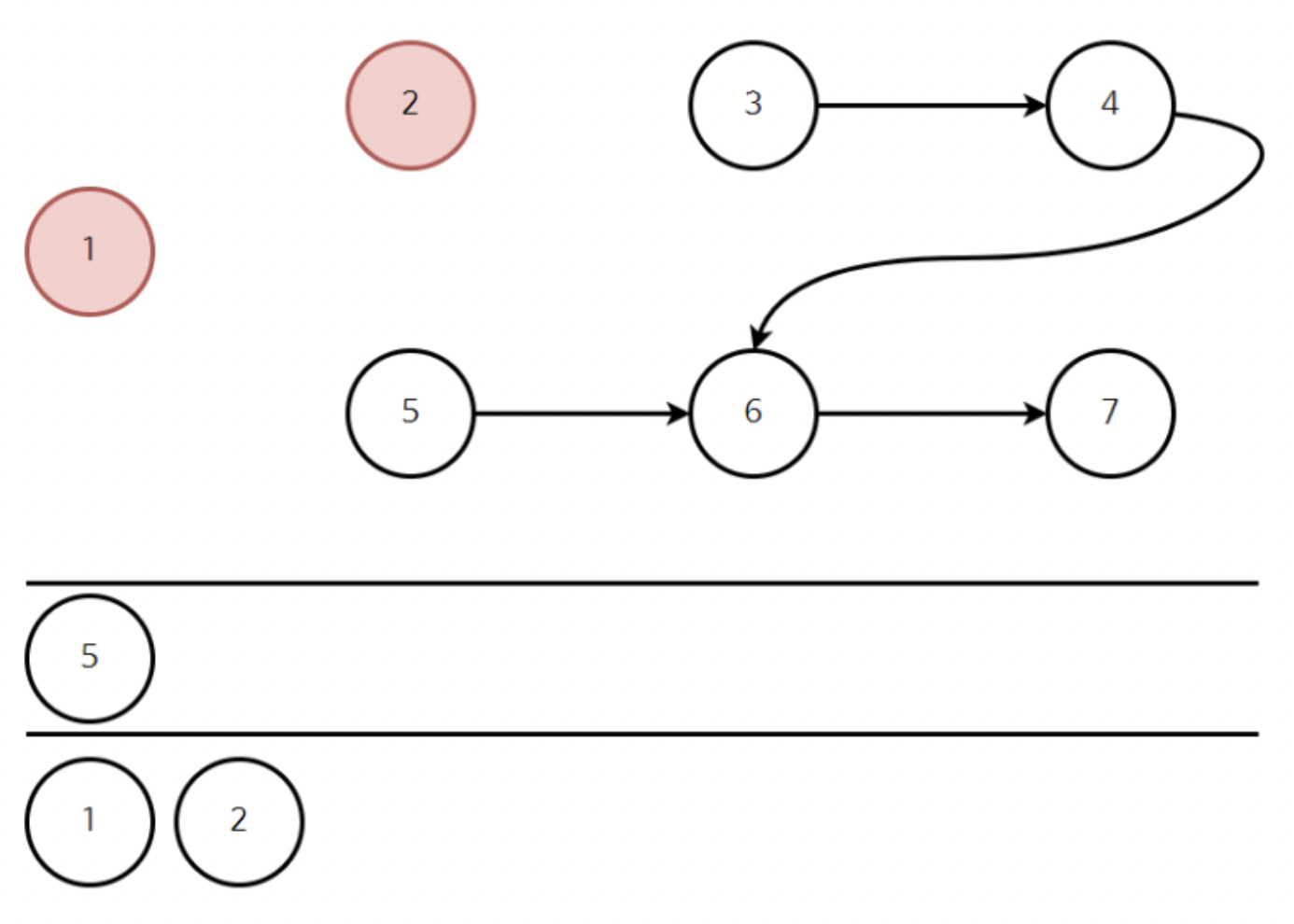
빼낸 뒤 결과는 위와 같다. 이후에 빼낸 2와 연결된 간선을 제거한 뒤 표를 다시 보자.

새롭게 정점 3의 진입차수가 0인 것을 확인했다.
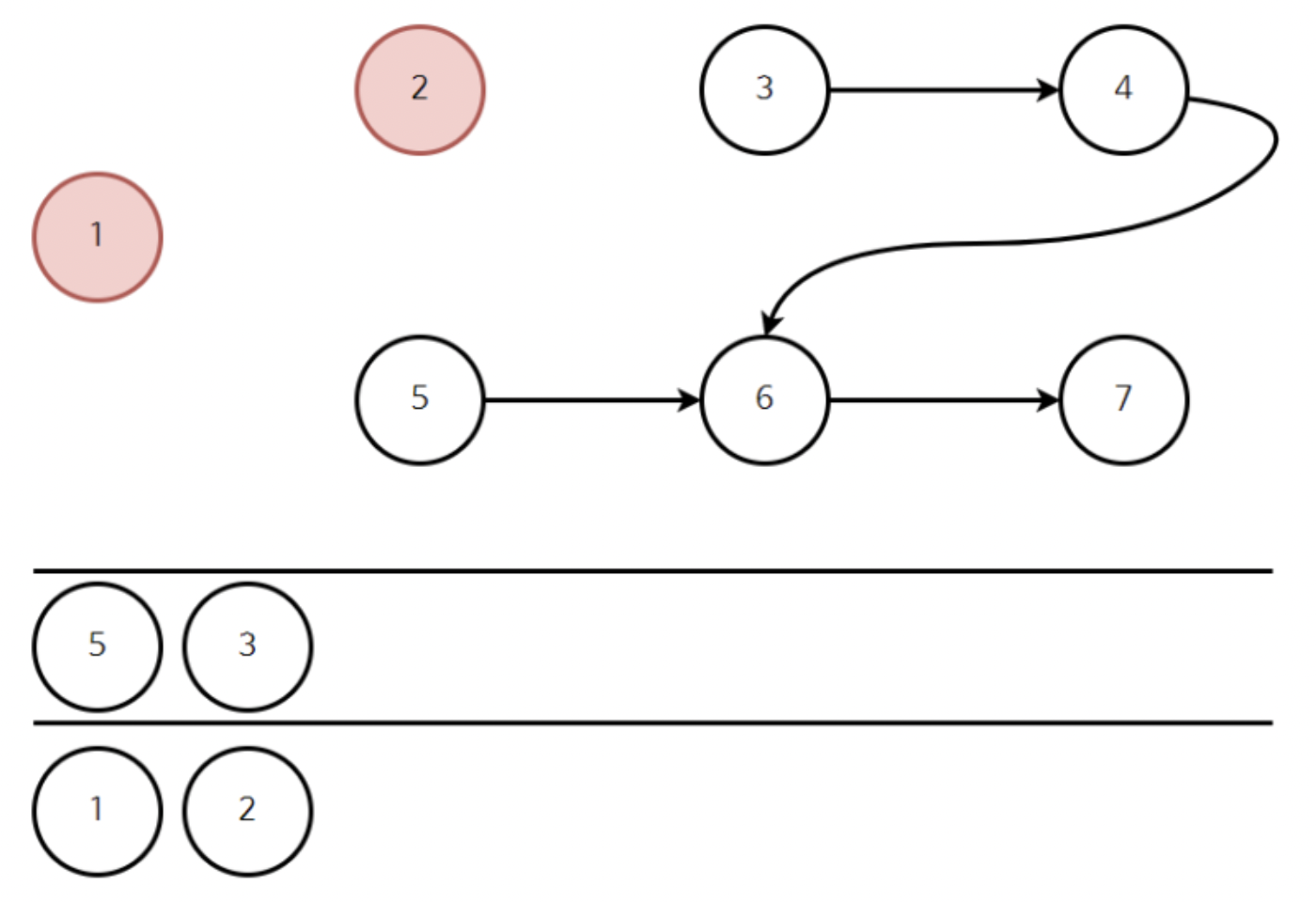
위와 같이 정점 3을 큐에 넣는다.
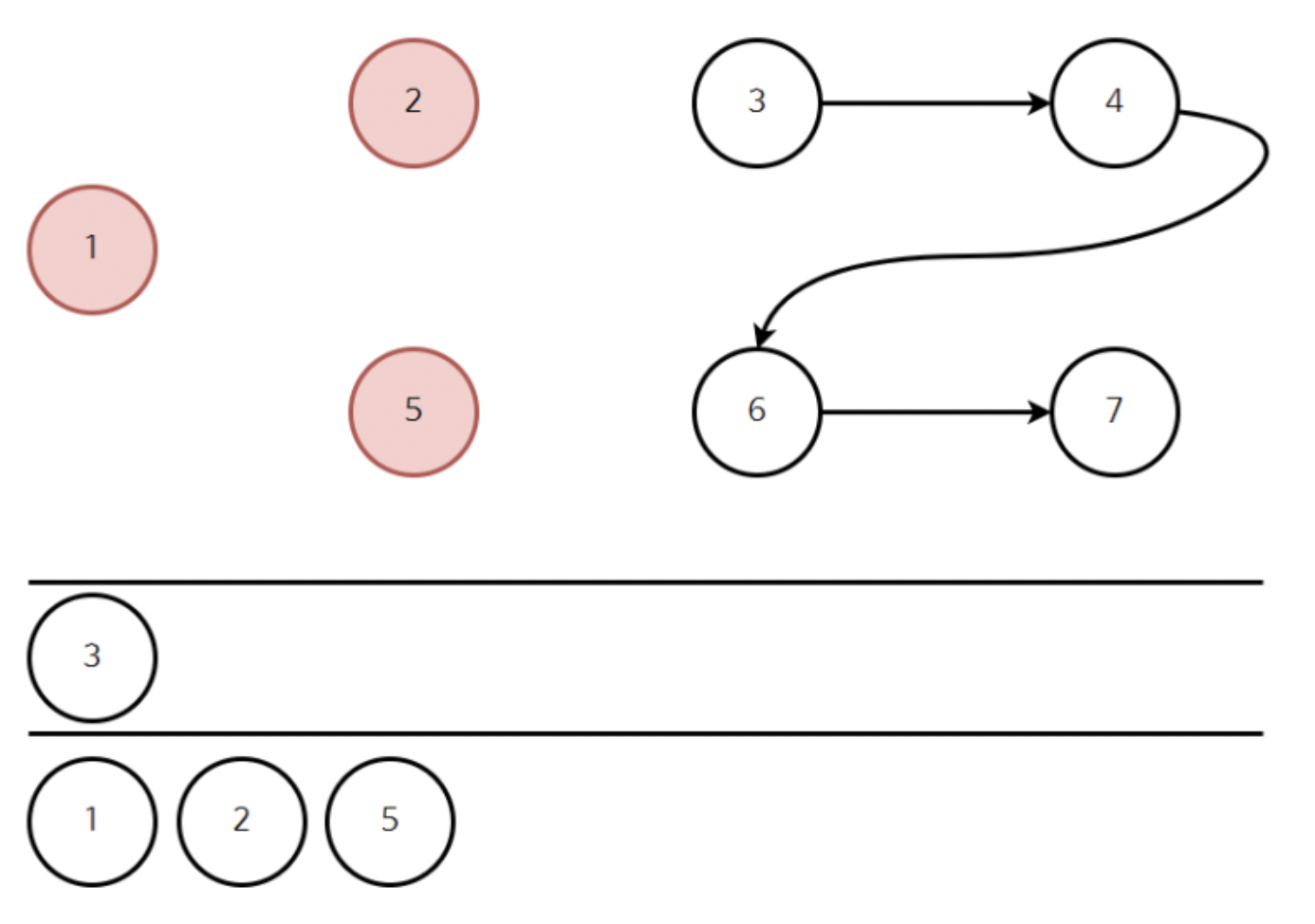
이후 위와 같이 5를 꺼낸 뒤, 5와 연결된 간선을 제거한다.

진입 차수가 0인 새로운 정점은 발견되지 않았다.
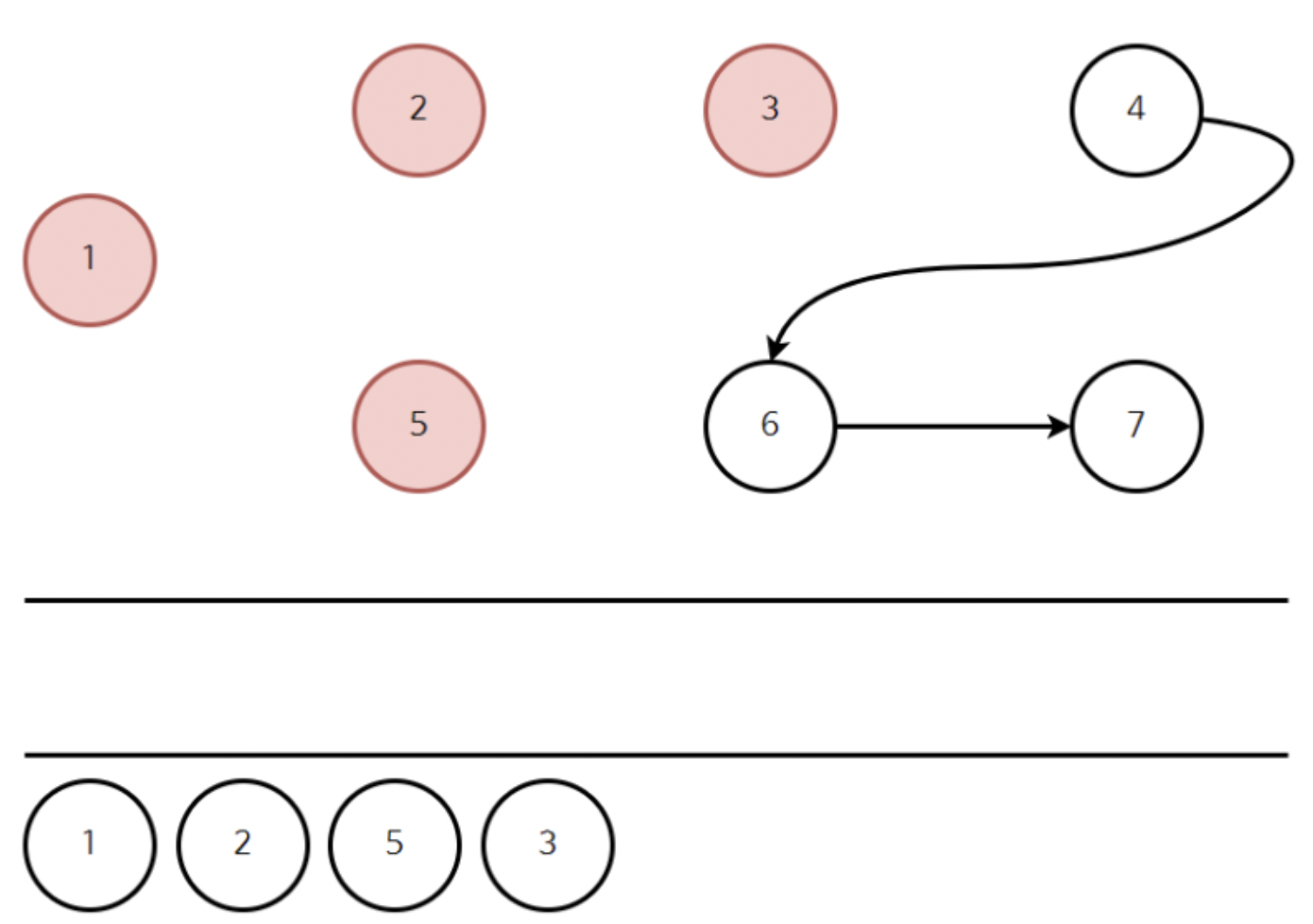
위와같이 3을 꺼내자.

진입차수가 0인 정점 4가 발견됐다.
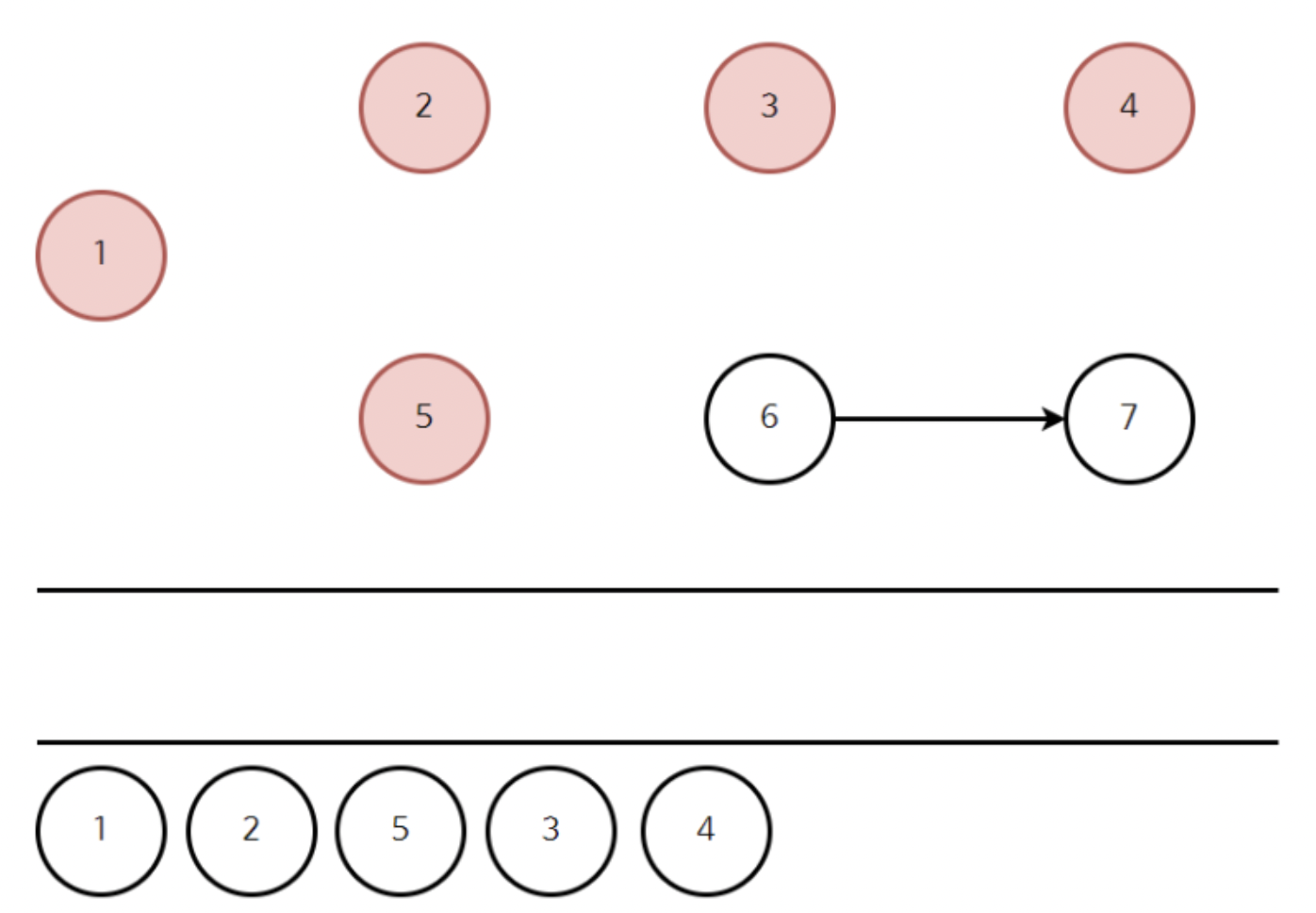
4를 큐에 넣고 바로 빼준 결과는 위와 같다.

이제 새롭게 정점 6이 진입차수 0으로 큐에 들어간다.
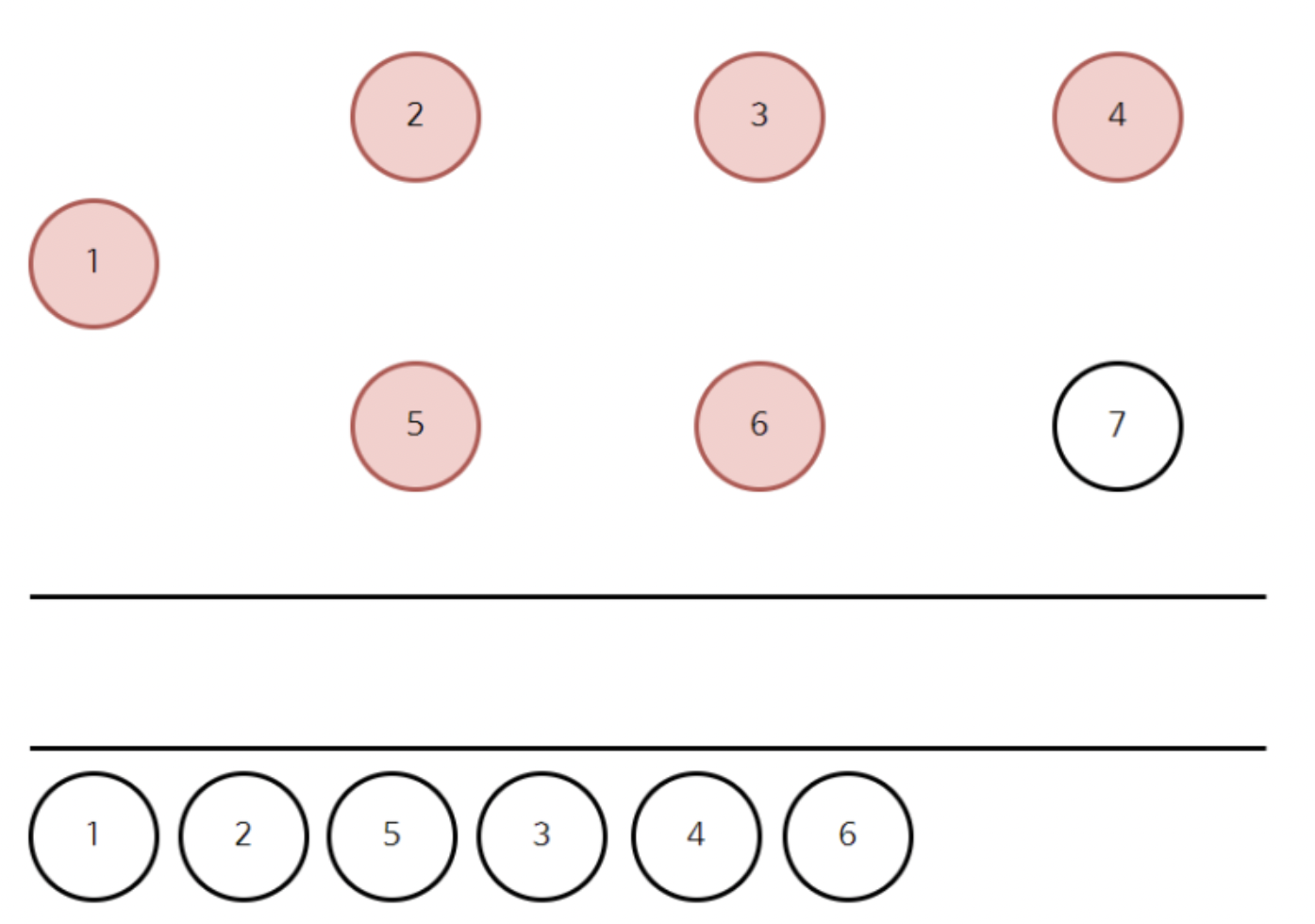
6을 처리한 결과는 위와 같다. 이제 진입 차수 표를 보자.

정점 7이 새롭게 진입차수 0이 되어서 큐에 들어간다.
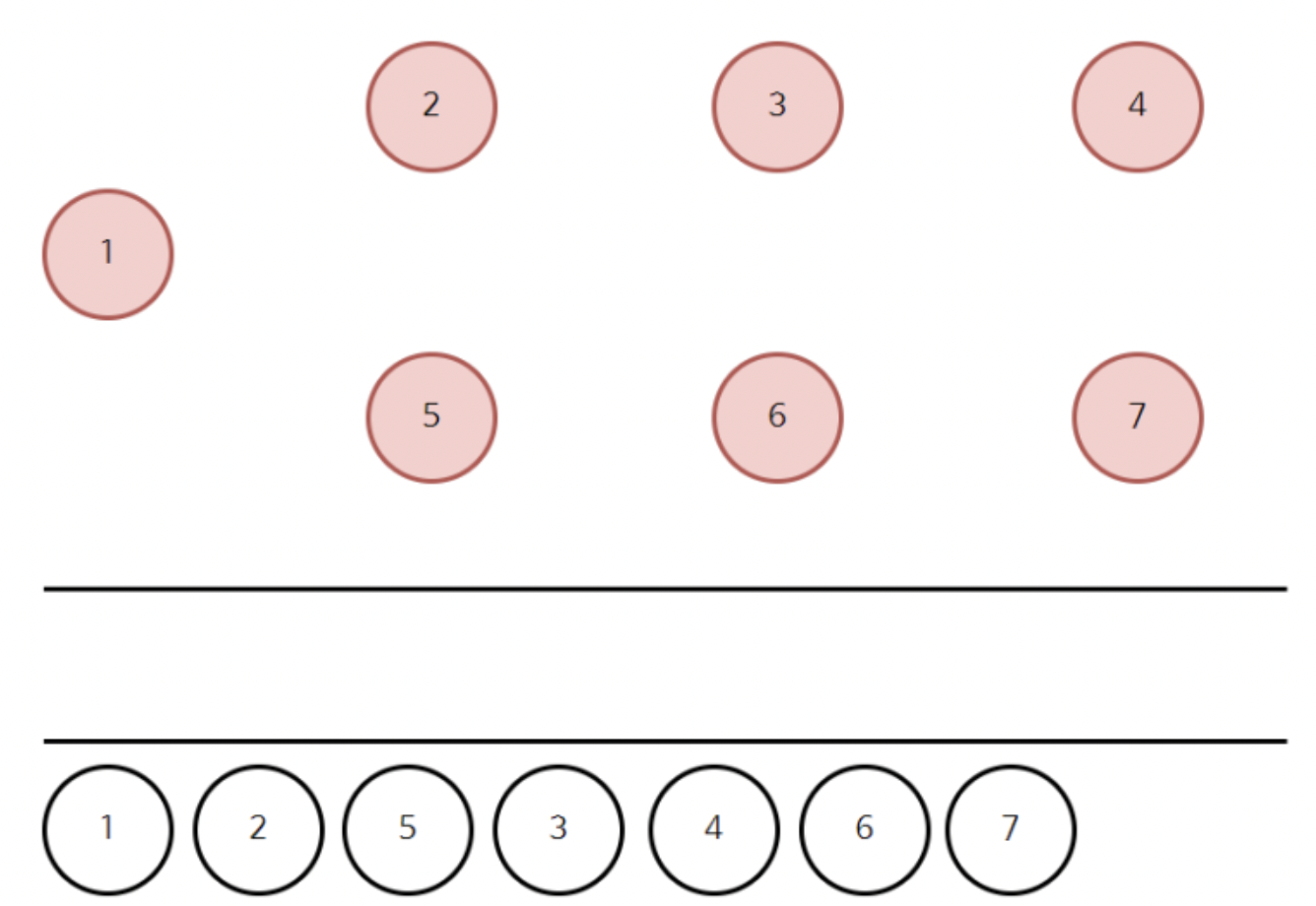
결과적으로 위와 같다.
정답은 큐에서 꺼낸 순서가 된다.
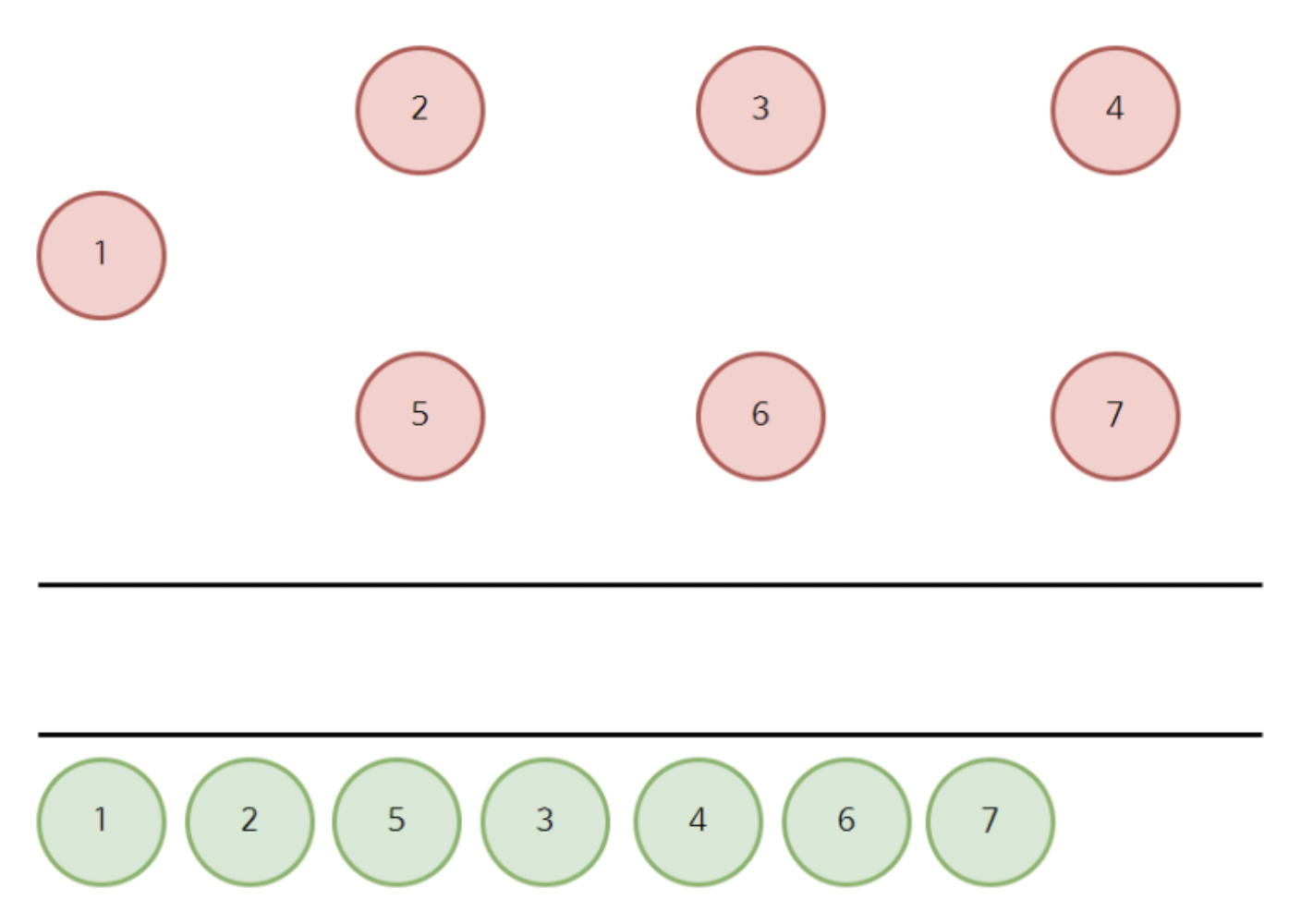
따라서 1->2->5->3->4->6->7이 정답이다.
구현
구현 방법에는 in_degree를 사용하는 BFS(Breath First Search) 방법과 DFS(Depth First Search)를 사용하는 방법이 있습니다.
정점의 위상 순서를 저장할 리스트 T를 사용하고, 정점 방문 여부를 저장하기 위해 visited [N] 배열을 사용합니다.
ArrayList로 그래프를 표현한다.
진입차수
자기 자신을 가리키는 에지의 개수
In-degree 방법 (BFS 방법)
정점에 들어오는 간선수를 저장하기 위해 indegree[N] 배열을 사용합니다.
여기서 i번째 요소는 정점 i로 들어오는 에지 수를 저장합니다.
동작 방식은 다음과 같습니다.
- 모든 정점의 indegree를 설정합니다.
-> ArrayList로 그래프를 표현할 때, 진입 차수 값을 계산한다. - in_degree가 0인 정점은 방문한 것으로 표시하고 큐에 정점을 추가합니다.
큐가 빌 때까지 순회하며 다음 작업을 수행합니다.
3.1. 큐의 앞 요소를 dequeue()로 가져와 result에 넣습니다.
3.2. dequeue()한 정점에 인접한 정점중 방문하지 않은 정점의 indegree를 하나 감소시킵니다.
3.3. indegree 감소 후 값이 0이면 해당 정점은 queue에 enqueue() 하고 방문한 것으로 표시합니다.
import java.util.*;
public class TopologicalSort {
static int n;
static int e;
public static void main(String[] args) {
n = 7; // 정점 갯수
e = 9; // 간선 갯수
int[] indegree = new int[n + 1];
List<List<Integer>> array = new ArrayList<List<Integer>>();
for (int i = 0; i < n + 1; i++)
array.add(new ArrayList<Integer>());
// 간선 목록 v1 -> v2
int[] v1 = {1, 1, 2, 4, 3, 3, 5, 2, 5};
int[] v2 = {2, 3, 5, 6, 4, 7, 6, 4, 4};
/**
* 1. v1 -> v2 인접리스트 생성
* 2. v2 를 가리키는 노드 갯수 indegree 증가
*/
for (int i = 0; i < e; i++) {
int c1 = v1[i];
int c2 = v2[i];
array.get(c1).add(c2);
indegree[c2]++;
}
topologicalSort(indegree, array);
}
static void topologicalSort(int[] indegree, List<List<Integer>> array) {
Queue<Integer> q = new LinkedList<Integer>();
Queue<Integer> result = new LinkedList<Integer>();
// 큐에 indegree 가 0 인 노드 담기
for (int i = 1; i < n + 1; i++) {
if (indegree[i] == 0) {
q.offer(i);
}
}
/**
* 1. 큐에서 값을 꺼내며 해당 노드가 가리키는 노드의 indegree 를 1 감소
* 2. 만약 indegree가 0 이 된다면 큐에 넣기
* 3. 큐가 빌때까지 반복
*/
while (!q.isEmpty()) {
int node = q.poll();
result.offer(node);
for (Integer i : array.get(node)) {
indegree[i]--;
if (indegree[i] == 0) {
q.offer(i);
}
}
}
System.out.println(result);
}
}참고
https://yoongrammer.tistory.com/86
do it 알고리즘 코딩 테스트 - 자바편
https://bcp0109.tistory.com/21
