계수 정렬(counting sort)
주어진 배열의 값 범위가 작은 경우 빠른 속도를 갖는 정렬 알고리즘이다. 최댓값과 입력 배열의 원소 값 개수를 누적합으로 구성한 배열로 정렬을 수행한다.
과정
-
입력 배열의 최댓값, Counting Array 생성
원소의 누적합을 구하기 위한 Counting Array 생성을 위해 입력 배열의 최댓값이 필요하다.
이후 '최댓값 + 1' 크기의 Counting Array를 생성하여 입력 배열의 값을 기준으로 조회된 좌표에 입력 배열의 각 원소 개수를 count 한다. -
입력 배열 원소 개수의 누적합
1번 과정에서 Counting Array 생성 및 원소 Count를 마쳤다면 이전 좌표의 원소 개수를 더해나가 누적합 배열로 만들어준다.
(현재 숫자 앞의 숫자들의 개수 + 현재 숫자 개수)
-> 헷갈리면 둘을 따로 만들어도 됨. -
입력 배열과 누적합 배열을 이용한 정렬 수행
입력 배열의 각 원소에 대해 Counting Array에 조회하여 어느 좌표에 들어가야 하는지 체크한 뒤 조회된 원소의 개수를 1 감소시켜 앞의 좌표로 입력받을 수 있게 한다. -
결과를 얻을 때, 해당 count배열과 sum배열의 값을 하나씩 줄이고 0 될 때 까지 반복한다.
큰 틀을 살펴보자.
배열을 정렬해보자. 우선 입력 배열 전체를 스캔해서 최대값 K를 찾고 Counting Array를 생성하며, 각 개수를 채워넣는다.
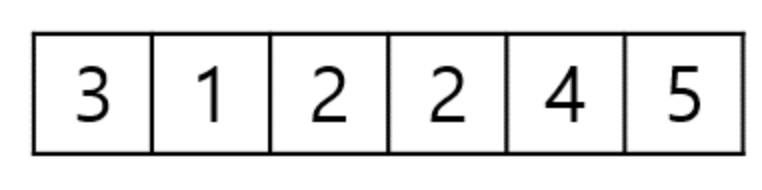
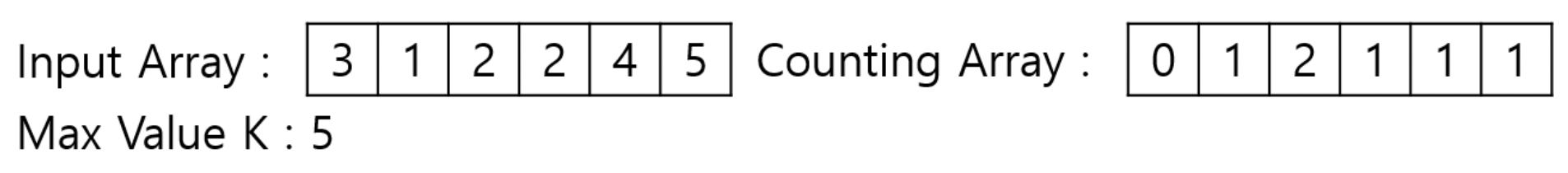
Counting Array를 누적합 배열로 바꿔준다.

이렇게 들으면 헷갈리니 예시로 확인해보자.
예시
주어진 데이터는 다음과 같다.

각 숫자가 몇번 나왔는지 count배열에 저장한다.

sum배열을 생성해 누적합을 저장한다.
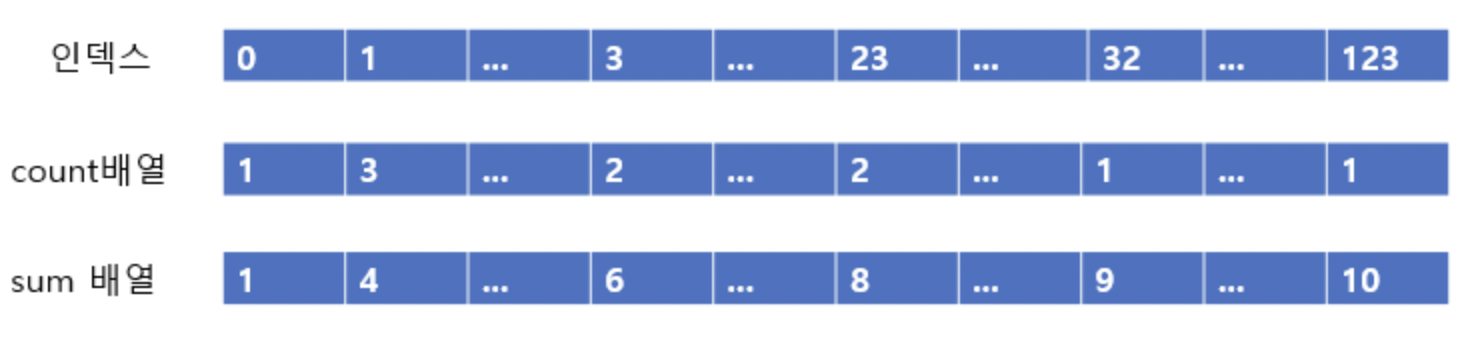
왜 sum배열이 필요할까?
현재 숫자가 정렬된 배열에 어디에 위치해야하는 지 표시한 것과 같기때문이다.
참고
stable과 unstable이 있다. stable은 정렬이 안된 배열에서 같은 숫자가 있을 때, 정렬할 때도 이 순서가 지켜짐을 의미한다.
예 ) [4, 1 , 2, 1] : 1이 두번 나오는데, 맨 처음에 나오는 1을 ㄱ1, 두번째에 나오는 1을 ㄴ1이라고 한다.
정렬 알고리즘을 돌리면
stable한 경우 : [ㄱ1,ㄴ1,2,4]
unstable한 경우 : [ㄴ1,ㄱ1,2,4]
이렇게 된다.
즉, 정렬하여 같은 숫자들의 위치가 바뀌냐 안바뀌냐에 따라 결정되는 것이다.
계수 정렬(counting sort)는 stable함을 유지하기위해 맨 뒤의 수부터 값을 채워준다.
만약 unstable해도 상관없다면 앞에서부터 채워도 문제가 될 것은 없다.
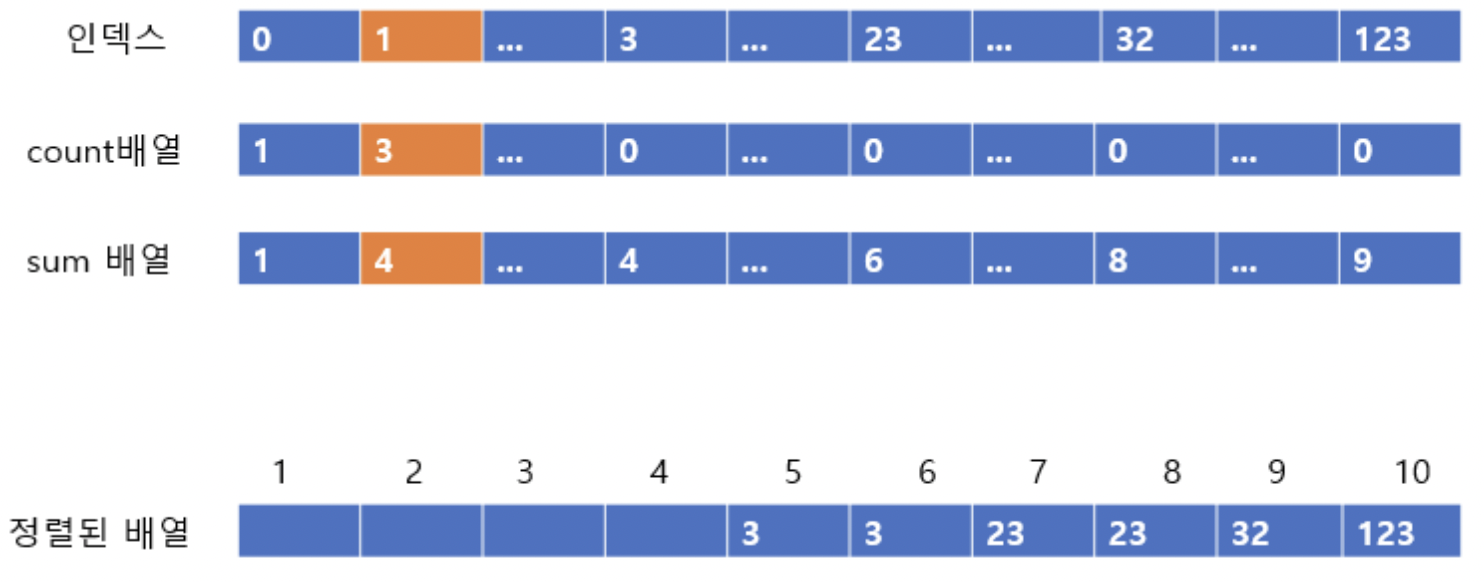
주황색으로 표시한 부분을 보자.
주황색 부분에서 인덱스 123은 count 배열에서 1이다. 즉 1개 있다는 것.
sum 배열에서는 10이다. 이는 자신이 있어야할 자리는 10번째라는 것이다.
따라서 아래에 정렬된 배열에 123을 10번째 인덱스에 넣어주고 count배열과 sum배열의 값을 줄여준다.
sum의 값에 해당하는 자리에 데이터를 넣고, 연산하다가 count가 0이되면 다음으로 넘어가면된다!
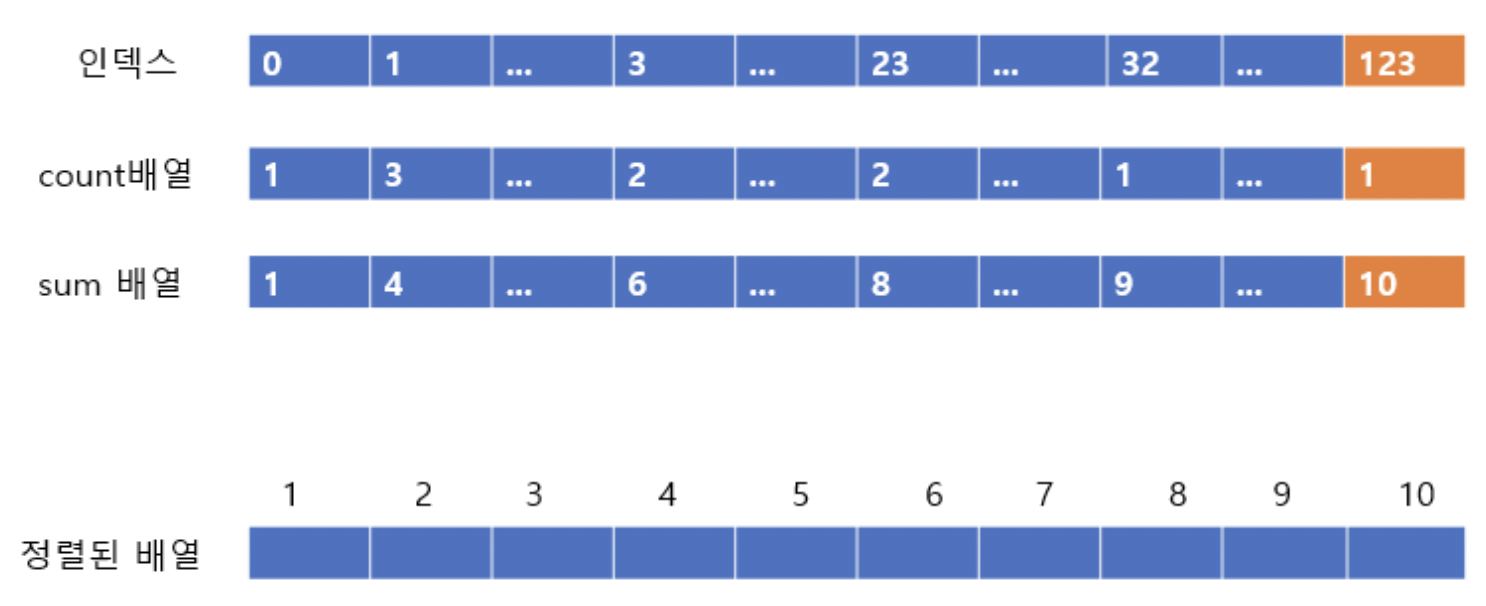
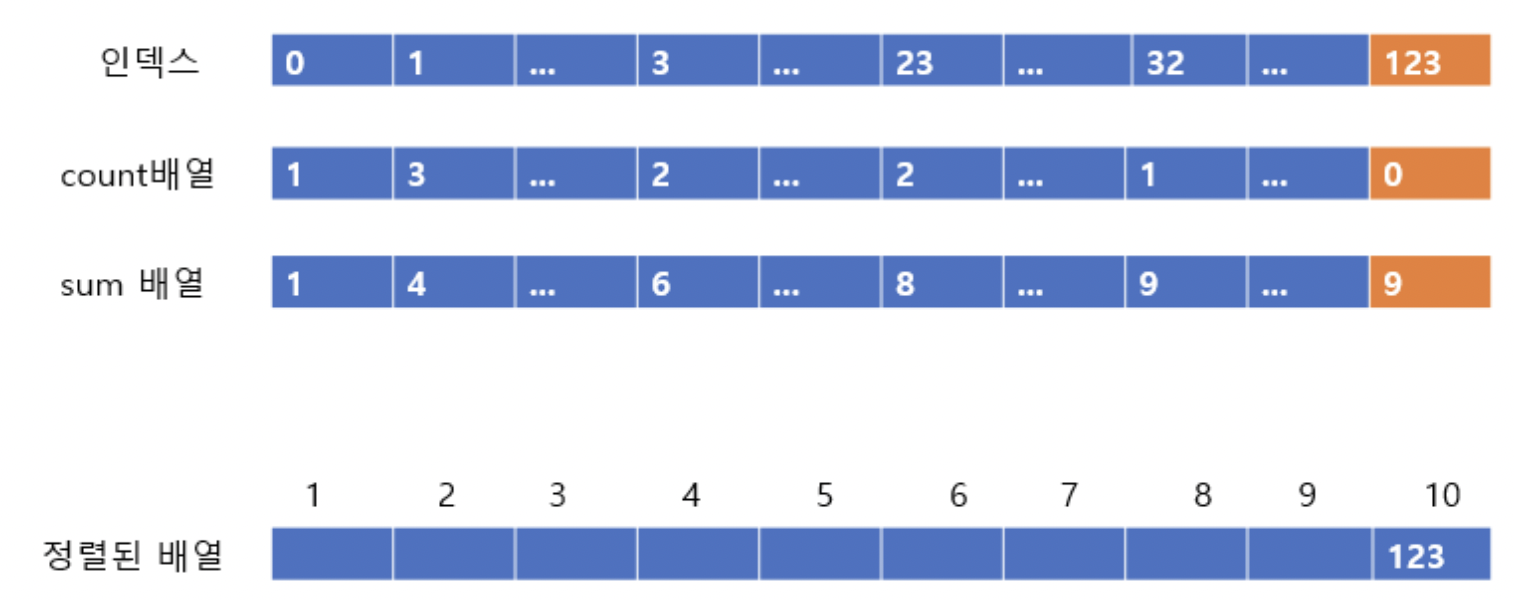
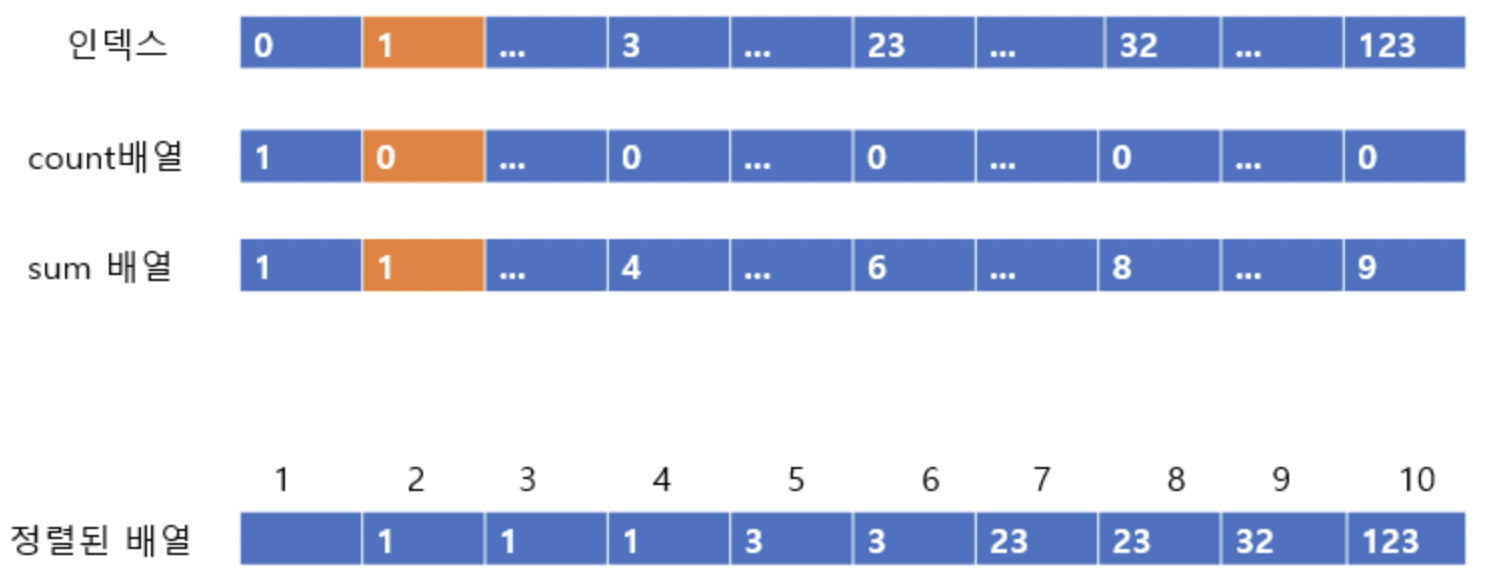
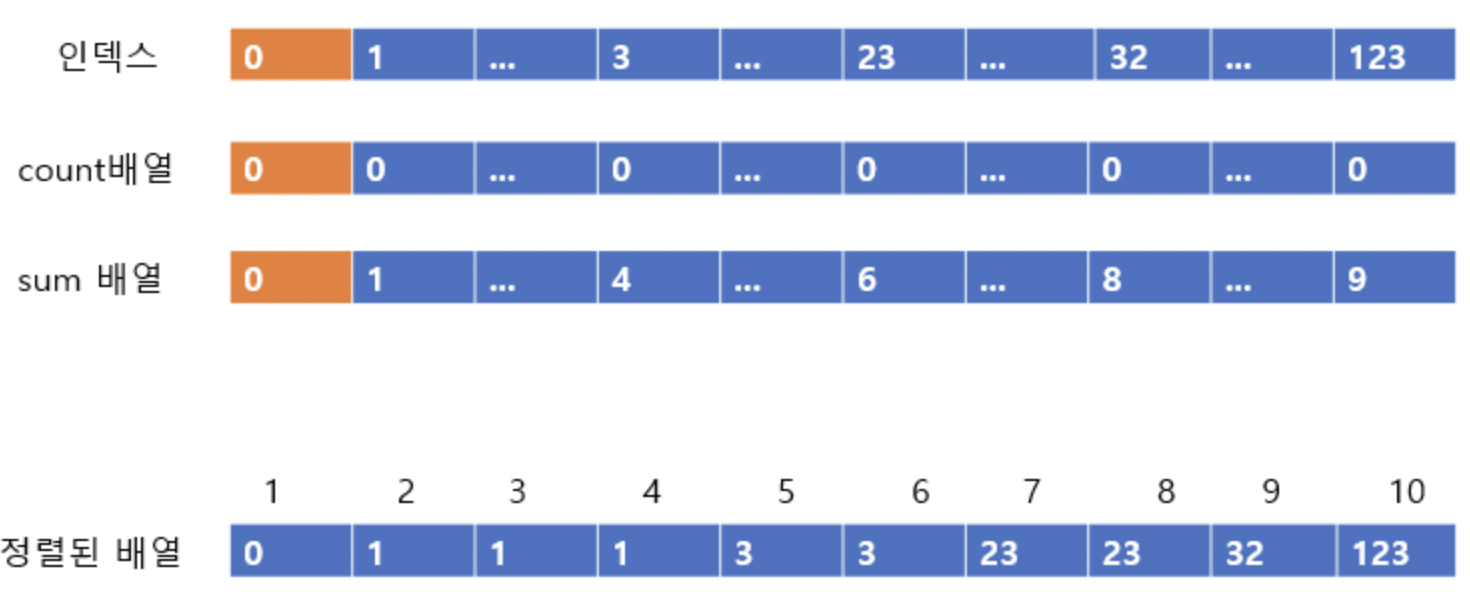
이후 각 자리마다 정렬된 사진을 올리겠다.
그 다음은 32가 정렬된 후이다. (count, sum이 알맞게 줄어든다)
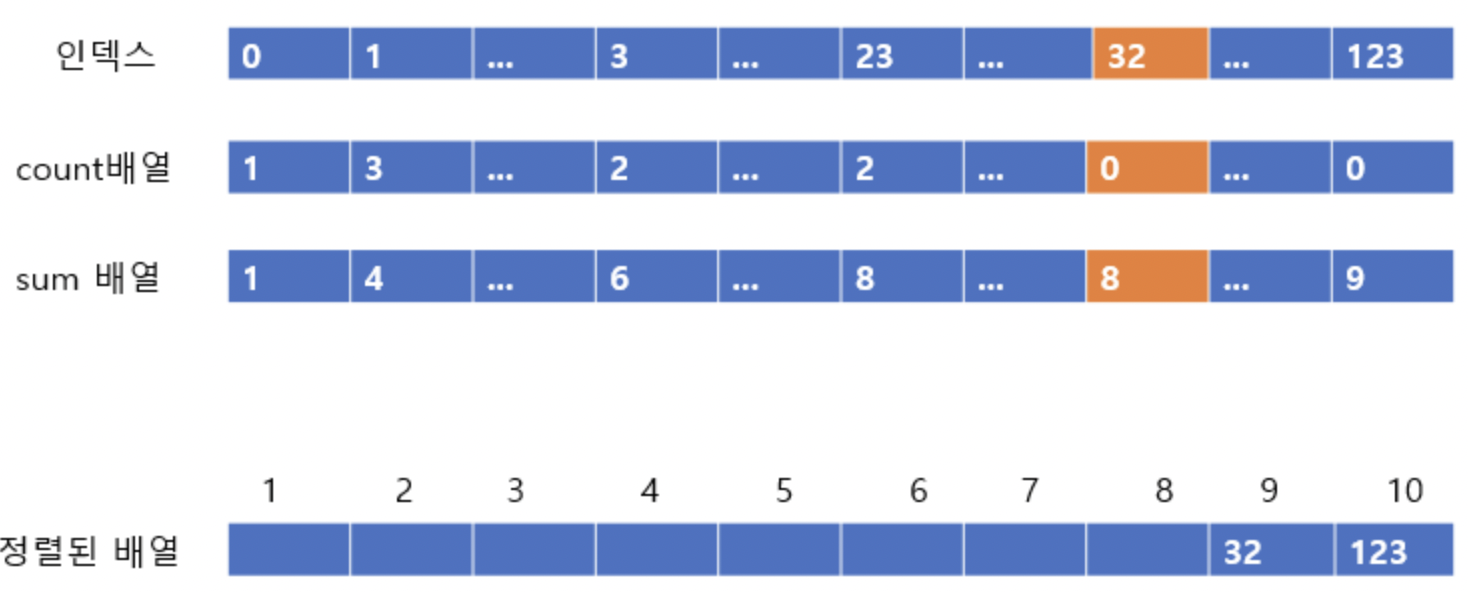
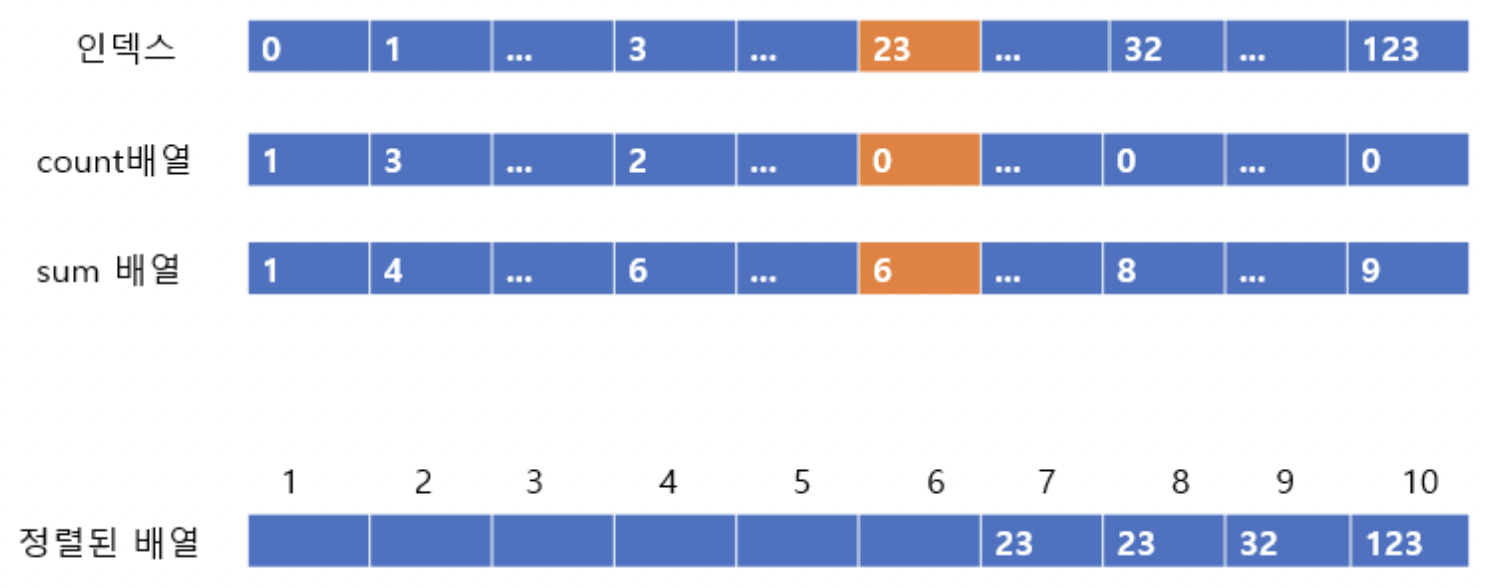
단점
잘 생각해보면 엄청난 메모리 낭비라는 것을 알 수 있다.
123사이즈의 메모리에서 사용한 메모리는 결국 0 , 1 , 3, 23, 32, 123 총 6개만 사용했다는 것을 알 수 있다. 이는 엄청난 메모리 낭비이다.
또한, 최대 단점으로는 숫자가 커지면 메모리가 너무 커져 사용할 수 없다는 단점과 음수가 있을 경우 사용하지 못한다는 단점이 있다.
쓰이는 상황
수능 시험 점수를 점수 별로 나열할 때를 생각해보자.
만약 수능 시험을 보는 인원이 50만 명이라고 하자.
50만명의 국어점수를 정렬하여 백분위를 구해야할 텐데, 50만명의 데이터를 정렬한다면 O(n^2)은 터무니 없고, O(nlogn)이나 O(n)안에 해결해야한다.
그런데, 잘 보면 수능 시험 점수라는 것은 음수도 없고 0~100까지의 점수만을 요구한다.
따라서 이를 계수 정렬로 정렬하는 것이 어렵지 않고 시간 복잡도 이득도 많이 볼 수 있어 사용하면 좋다.
이렇게 명확한 데이터의 제한이 있다면 계수 정렬은 O(nlogn)정렬보다 더 큰 이득을 볼 수 있다.
시간복잡도
O(n+k)
(k = 최대수)
정렬 과정을 살펴보면 만약 최대값이 주어지지 않은 경우 전체 배열을 탐색해야 하므로
O(n)이 소요되고, Counting Array에 개수를 count하는 과정도 O(n)이 소요된다.
이후 출력 배열에 값을 입력하여 정렬된 배열을 얻는 과정에도 O(n)이 소요된다.
따라서 시간 복잡도는 O(n)이 된다.
그러나, 배열의 길이와 상관없이 배열의 최댓값 K가 정렬 시간의 변수로 작용하며 배열의 길이가 작은데, K가 굉장히 클 경우 정렬 시간은 K에 종속된다.
따라서, 일반적으로 카운팅 정렬의 시간복잡도는 O(n+k)라고 말한다.
그리고 K가 최대한 작아야 유리하므로 입력값의 범위가 작을 때 높은 효율을 보인다.