삽입 정렬
이미 정렬된 데이터 범위에 정렬되지 않은 데이터를 적절한 위치에 삽입시켜 정렬하는 방식
특징
- 정렬이 진행됨에 따라 왼쪽에는 정렬이 종료된 값이 모이게 되고, 오른쪽에는 아직 정렬되지 않은 값이 남게 된다.
- 선택 정렬은 최소값 검색이 필요하지만 삽입 정렬은 필요 없다.
- 삽입 정렬은 평균 시나리오에서 선택 정렬과 유사하고(데이터 정렬 유형에 따라 차이가 있다) 버블 정렬보다 빠르다.
- 삽입 정렬은 데이터를 '비교'하면서 찾기 때문에 '비교 정렬'이며 정렬의 대상이 되는 데이터 외에 추가적인 공간을 필요로 하지 않기 때문에 '제자리 정렬(in-place sort)'이기도 하다.
-> 정확히는 데이터를 서로 교환하는 과정(swap)에서 임시 변수를 필요로 하나, 이는 충분히 무시할 만큼 적은 양이기 때문에 제자리 정렬로 본다 - 타겟 숫자가 이전 숫자보다 크기 전까지 반복하기 때문에 이미 정렬이 되어있는 경우 항상 타겟숫자가 이전 숫자보다 크다.
-> 값을 N번만 비교하기 때문에 최선의 경우 O(N)의 시간 복잡도를 갖게 되는 것이다.
-> 반대로 최악의 경우는 타겟 숫자가 이전 숫자보다 항상 작기 때문에 결국 N 번째 숫자에 대하여 N-1 번을 비교해야 한다. 그렇기 때문에 최악의 경우는 O(N2)의 시간복잡도를 보인다. - Bubble Sort나 Selection Sort 와 이론상 같은 시간복잡도를 갖음에도 평균 비교 횟수에 대한 기대값이 상대적으로 적기 때문에 평균 시간복잡도가 O(N2) 인 정렬 알고리즘 중에서는 빠른편에 속하는 알고리즘이다.
장점
- 추가적인 메모리 소비가 작다.
- 거의 정렬 된 경우 매우 효율적이다. 즉, 최선의 경우 O(N)의 시간복잡도를 갖는다.
- 안정정렬이 가능하다.
시간 복잡도
O(n^2) : 느린편
현재 리스트의 데이터가 거의 정렬된 상태라면 매우 빠르게 동작한다.
최선의 경우 O(n)의 시간복잡도를 가진다.
핵심이론
선택 데이터를 현재 정렬된 데이터 범위 내에서 적절한 위치에 삽입!
앞에서부터 해당 원소가 위치 할 곳을 탐색하고 해당 위치에 삽입
과정
- 현재 index에 있는 데이터 값을 선택한다. (첫 번째 타겟은 두 번째 원소부터 시작한다.)
- 현재 선택한 데이터가 정렬된 데이터 범위에 삽입될 위치를 탐색한다.
- 삽입 위치부터 index에 있는 위치까지 shift연산을 수행한다.
- 삽입 위치에 현재 선택한 데이터를 삽입하고, index++연산을 수행한다.
- 전체 데이터의 크기만큼 index가 커질때 까지, 즉 선택할 데이터가 없을 때까지 반복한다.
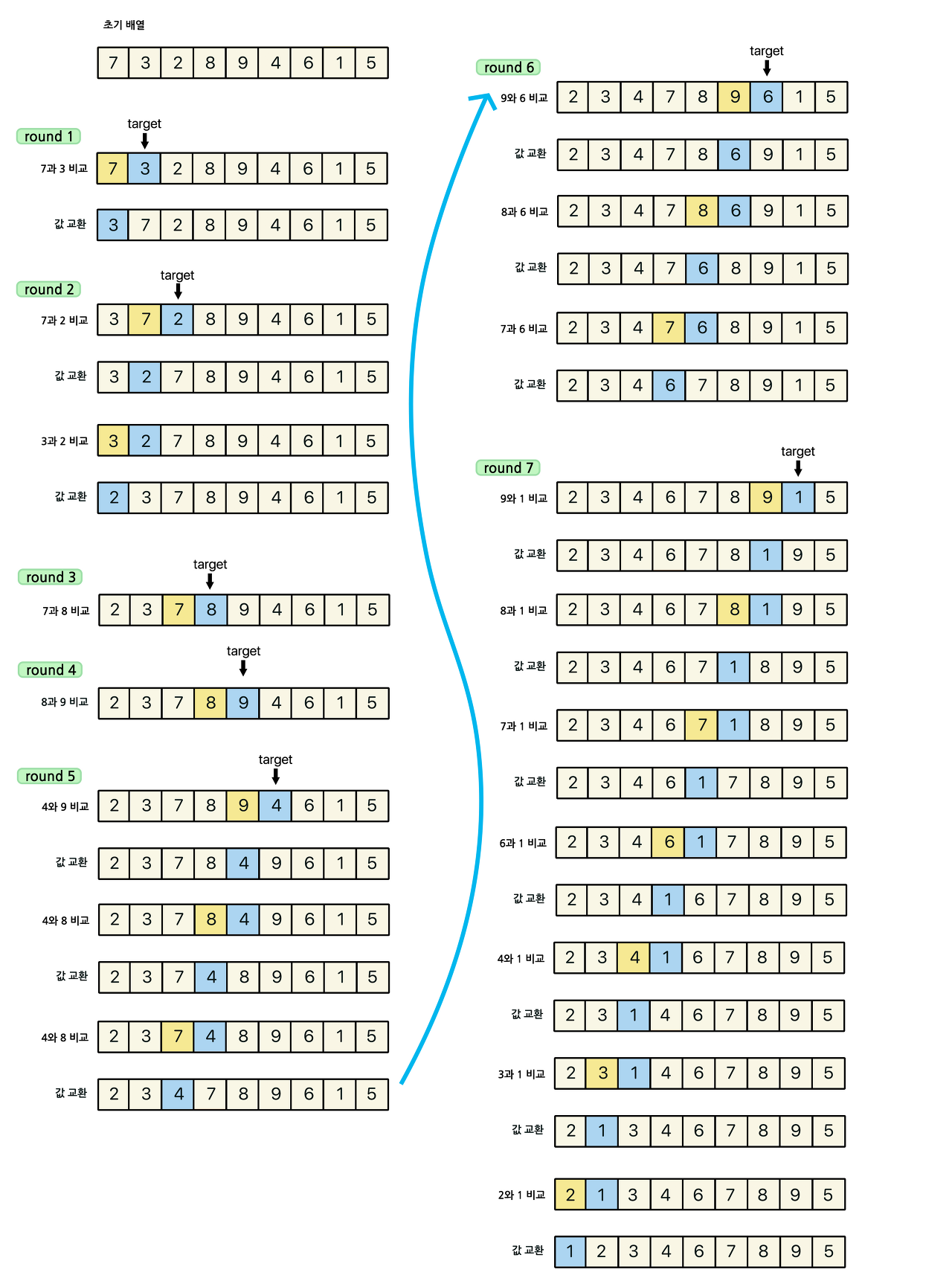
구현
public class Insertion_Sort {
public static void insertion_sort(int[] a) {
insertion_sort(a, a.length);
}
private static void insertion_sort(int[] a, int size) {
for(int i = 1; i < size; i++) {
// 타겟 넘버
int target = a[i];
int j = i - 1;
// 타겟이 이전 원소보다 크기 전 까지 반복
while(j >= 0 && target < a[j]) {
a[j + 1] = a[j]; // 이전 원소를 한 칸씩 뒤로 미룬다.
j--;
}
/*
* 위 반복문에서 탈출 하는 경우 앞의 원소가 타겟보다 작다는 의미이므로
* 타겟 원소는 j번째 원소 뒤에 와야한다.
* 그러므로 타겟은 j + 1 에 위치하게 된다.
*/
a[j + 1] = target;
}
}
}Tip
적절한 삽입 위치를 탐색하는 부분에서 이진탐색 등과 같은 탐색 알고리즘을 사용하면 시간 복잡도를 줄일 수 있다.
