[알고리즘] 정렬 - 퀵정렬

Benjamin·2022년 12월 19일

목록 보기

7/25

가장 유명한 정렬 알고리즘중 하나인 퀵정렬에 대해 알아보자

퀵정렬

Stable Sort (X)
분할 정복 (Devide and Conquer) 기법과 재귀 알고리즘을 이용한 정렬 알고리즘
기준값을 선정해 해당 값보다 작은 데이터와 큰 데이터로 분류하는 것을 반복해 정렬
기준값이 어떻게 되는가? -> 시간 복잡도에 많은 영향을 줌
평균 시간복잡도 = O(nlogn)

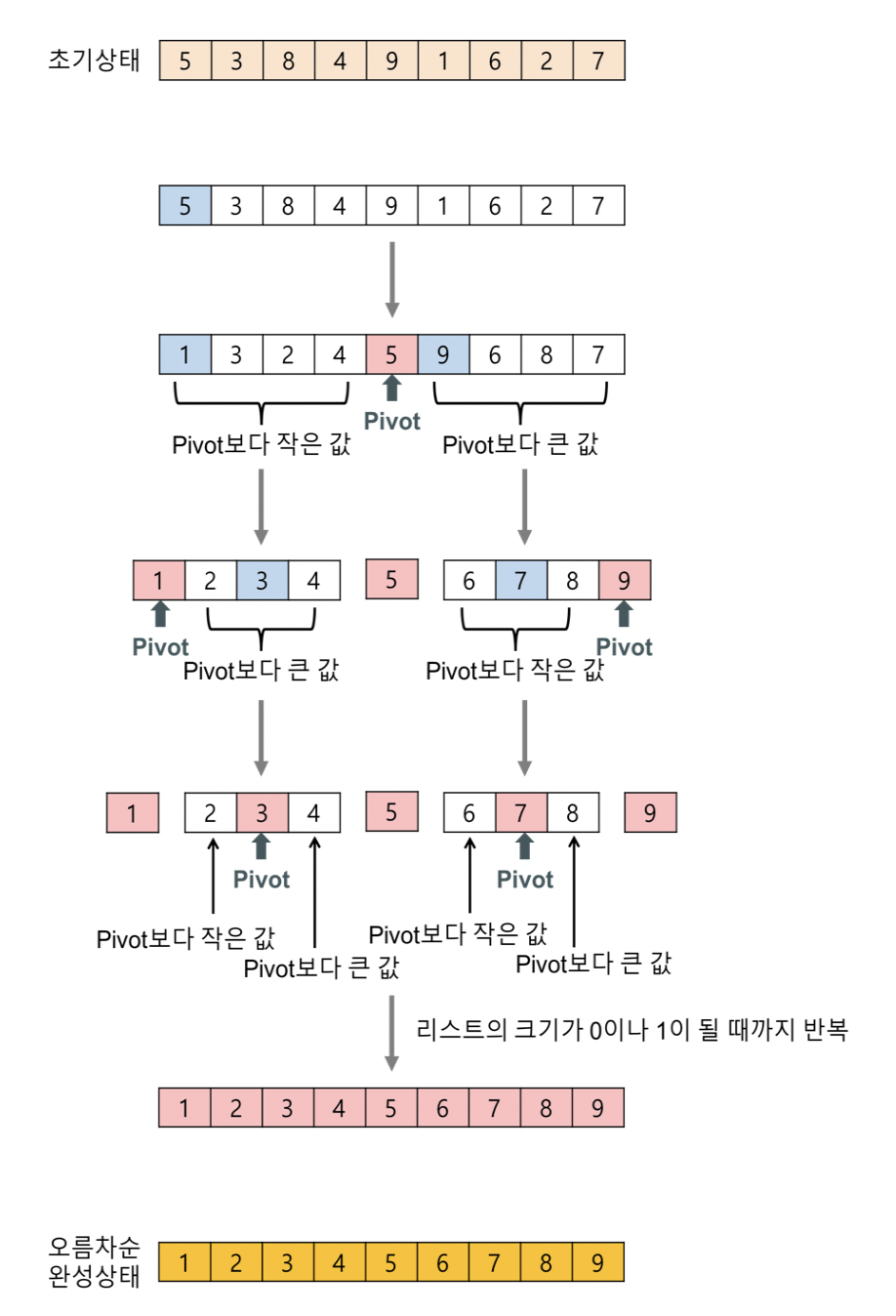
분할(Divide): 입력 배열을 피벗을 기준으로 비균등하게 2개의 부분 배열(피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)로 분할한다.
정복(Conquer): 부분 배열을 정렬한다. 부분 배열의 크기가 충분히 작지 않으면 순환 호출 을 이용하여 다시 분할 정복 방법을 적용한다.

순환 호출이 한번 진행될 때마다 최소한 하나의 원소(피벗)는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.

-> 시간복잡도가 준수하여 코테에서도 종종 응용한다. 재귀 함수 형태로 직접 구현하는게 중요!

핵심이론

pivot을 중심으로 계속 데이터를 2개의 집합으로 나누면서 정렬하는 것

<pivot 정하는 법>
pivot == K : K번째 수를 찾은 것이므로 알고리즘 종료
pivot > K : pivot의 왼쪽 부분에 K가 있으므로 왼쪽(S~pivot-1)만 정렬 수행
pivot < K : pivot의 오른쪽 부분에 K가 있으므로 오른쪽(pivot+1 ~ E)만 정렬 수행

정렬 과정

pivot 설정
pivot 기준으로 다음 a~e과정을 거쳐 데이터를 2개의 집합으로 분리한다.
a. start가 가리키는 데이터가 pivot이 가리키는 데이터보다 작으면 start를 오른쪽 1칸 이동
b. end가 가리키는 데이터가 pivot이 가리키는 데이터보다 크면 end를 왼쪽으로 1칸 이동
c. start가 가리키는 데이터가 pivot이 가리키는 데이터보다 크고, end가 가리키는 데이터가 pivot이 가리키는 데이터보다 작으면 start,end가 가리키는 데이터를 swap하고 start는 오른쪽, end는 왼쪽으로 1칸씩 이동
d. start와 end가 만날 때까지 a~c 반복
e. start, end가 만나면 만난 지점에서 가리키는 데이터와 pivot이 가리키는 데이터를 비교하여 pivot이 가리키는 데이터가 크면 만난 지점의 오른쪽에, 작으면 만난 지점의 왼쪽에 pivot이 가리키는 데이터를 삽입한다.
분리 집합에서 각각 다시 pivot을 선정한다.
분리 집합이 1개 이하가 될 때까지 과정 1~3을 반복한다.

예시

[6, 5, 1, 4, 7, 2, 3]이 있다고 가정하자.

피봇(pivot)이라고 불리는 임의의 기준값을 사용합니다.
pivot 값을 선택하는데는 여러가지 방법이 있지만 여기서는 간단한 설명을 위해 정 중앙에 위치한 4을 pivot으로 정하겠습니다.
그리고 다음과 같이 이 pivot 값을 기준으로 pivot보다 작은 값의 그룹과 pivot보다 큰 값의 그룹으로 나눕니다.

[3, 2, 1] < 4 < [7, 5, 6]
위와 같이 pivot 값보다 작은 값들은 모두 왼편으로 몰고, 큰 값들은 모두 오른편으로 몰면 기준값은 정확히 정렬된 위치에 놓이게 됩니다.
또한 이런 방식으로 분할을 해놓으면 앞으로 더 이상 왼편에 있는 값들과 오른편에 있는 값들 간에는 비교를 할 필요가 없습니다.
따라서 반대편은 전혀 신경쓰지 않고 왼편이든 오른편이든 같은편 내의 값들 끼리만 비교 후 정렬을 할 수 있게 됩니다.

먼저 왼편을 동일한 방식으로 정렬해보도록 하겠습니다. 왼편의 정 가운데에 위치한 pivot 값인 2 보다 작은 값인 1인 왼쪽에 큰 값인 3은 오른쪽에 위치시켰습니다. 이제 양쪽 모두 값이 하나씩 밖에 없기 때문에 이로써 왼편의 정렬 작업은 완료되었습니다.

[1] < 2 < [3]

오른편도 동일한 방식으로 정렬해보겠습니다.
오른편의 pivot 값인 5 보다 작은 값은 없으므로 7과 6을 모두 오른편에 위치시켰습니다.
[] < 5 < [7, 6]

5의 오른편에는 값이 2개가 있기 때문에 추가 정렬이 필요합니다.

[6] < 7 < []
마지막으로 지금까지 좌우로 분할했던 값들을 모두 합치보면 다음과 같이 정렬된 배열을 얻을 수 있습니다.

[1, 2, 3, 4, 5, 6, 7]
지금까지 살펴본 것과 같이 퀵 정렬은 배열을 pivot 값 기준으로 더 작은 값과 큰 값으로 반복적으로 분할하여 정렬해나가는 방식을 취하고 있습니

특징

자바의 Arrays.sort()처럼 지원되는 내장 정렬 함수 : 대부분은 퀵 정렬을 기본으로 한다.
일반적으로 원소의 개수가 적을수록 나쁜 중간값이 선택될 확률이 높아지기 때문에, 원소의 개수에 따라 퀵 정렬에 다른 정렬을 혼합해서 쓰는 경우가 많다.
병합 정렬과 퀵 정렬은 분할 정복과 재귀 알고리즘을 사용한다는 측면에서는 유사해보이지만, 내부적으로 정렬하는 방식에서 큰 차이가 있습니다.
병합 정렬은 항상 정 중앙을 기준으로 단순 분할 후 병합 시점에서 값의 비교 연산이 발생하는 반면, 퀵 정렬은 분할 시점부터 비교 연산이 일어나기 때문에 그 이후 병합에 들어가는 비용이 매우 적거나 구현 방법에 따라서 아예 병합을 하지 않을 수도 있습니다.
시간 복잡도가 O(nlog₂n)를 가지는 다른 정렬 알고리즘과 비교했을 때도 가장 빠르다.
퀵 정렬이 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환할 뿐만 아니라, 한 번 결정된 피벗들이 추후 연산에서 제외되기 때문이다.

복잡도

<이상적인 경우>
pivot 값을 기준으로 동일한 개수의 작은 값들과 큰 값들이 분할되어 O(nlog(n))의 시간 복잡도

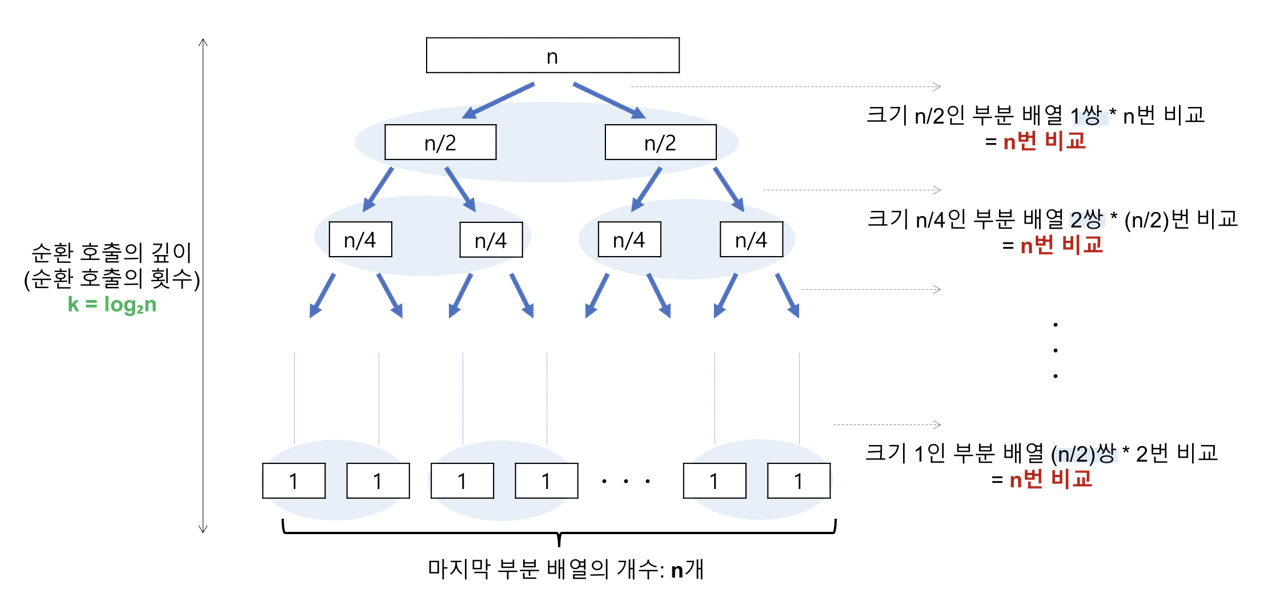
순환 호출의 깊이
레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, n=2^3의 경우, 2^3 -> 2^2 -> 2^1 -> 2^0 순으로 줄어들어 순환 호출의 깊이가 3임을 알 수 있다. 이것을 일반화하면 n=2^k의 경우, k(k=log₂n)임을 알 수 있다.
각 순환 호출 단계의 비교 연산
각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.
순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = nlog₂n
이동 횟수
비교횟수보다 적으므로 무시할 수 있다.

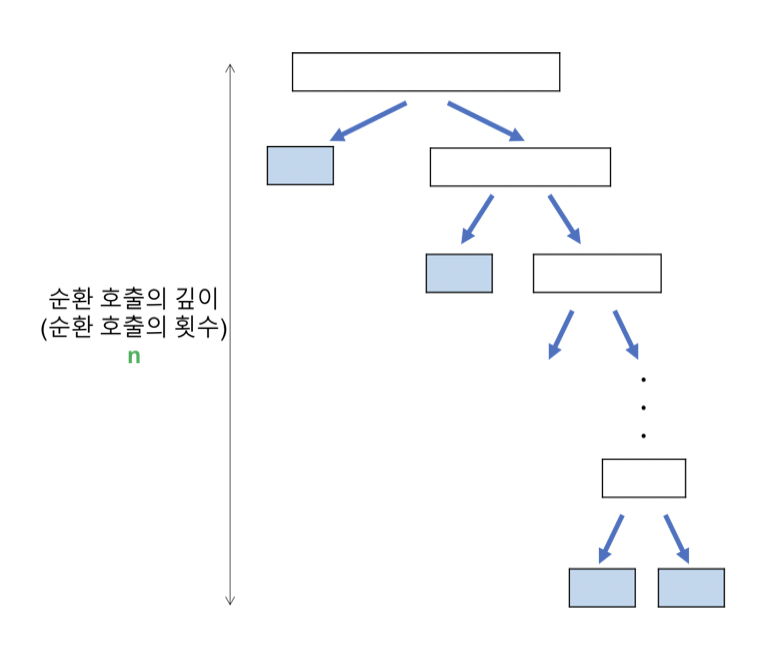
<최악의 경우>
O(n^2)의 시간 복잡도
리스트가 계속 불균형하게 나누어지는 경우 (특히, 이미 정렬된 리스트에 대하여 퀵 정렬을 실행하는 경우)

순환 호출의 깊이
레코드의 개수 n이 2의 거듭제곱이라고 가정(n=2^k)했을 때, 순환 호출의 깊이는 n임을 알 수 있다.
각 순환 호출 단계의 비교 연산
각 순환 호출에서는 전체 리스트의 대부분의 레코드를 비교해야 하므로 평균 n번 정도의 비교가 이루어진다.
순환 호출의 깊이 * 각 순환 호출 단계의 비교 연산 = n^2
이동 횟수
비교 횟수보다 적으므로 무시할 수 있다.

따라서 상용 코드에서는 중앙값(median)에 가까운 pivot 값을 선택할 수 있는 섬세한 전략이 요구되며, 배열의 첫값과 중앙값 그리고 마지막값 중에 크기가 중간인 값을 사용하는 방법이 많이 사용됩니다.
퀵 정렬은 공간 복잡도는 구현 방법에 따라 달라질 수 있는데, 입력 배열이 차지하는 메모리만을 사용하는 in-place sorting 방식으로 구현을 사용할 경우, O(log(n))의 공간 복잡도를 가진 코드의 구현이 가능합니다.
(순환 호출의 깊이를 말하는것같다.)

-> 코테에서 STL을 사용할 수 없으면, 최악의 경우가 있으므로 퀵정렬은 절대 사용하면 안된다!!! 비슷한 시간복잡도 O(NlogN)을 가지는 병합정렬이나 힙정렬을 사용하도록하자!