java에서는 변환에 사용할 수 있는 메소드 제공하고있고, 알고리즘인가 싶겠지만(?) 코테에 꽤 자주나오는걸로 알고있어서 따로 정리한다.
10진법에서 N진법으로, N진법에서 10진법으로 변환하는 방법을 알아보자.
10진법에서 N진법으로 변환하기
수학으로 생각하면 10진법으로 표기된 숫자를 N으로 나누어 그 나머지를 표시하고 더 이상 나눌 수 없을 때까지 반복하여 표기하는 방식이다.
예를 들어 10진법 5를 3진법으로 바꾼다면, 5를 3으로 나누면 나머지 2에 몫은 1이다.
최종 몫부터 표시하므로 12가 된다.
이를 자바 코드로 살펴보자.
public class Conversion {
public static void main(String[] args) {
int number = 127; // 진법 변환할 숫자
conversion(number, 2); // 2진법 변환
conversion(number, 3); // 3진법 변환
conversion(number, 4); // 4진법 변환
conversion(number, 5); // 5진법 변환
conversion(number, 8); // 8진법 변환
conversion(number, 16); // 16진법 변환
// 이외 자바 내에서 제공하는 방식을 사용 시,
System.out.println(Integer.toBinaryString(number)); // 2진법 변환
System.out.println(Integer.toOctalString(number)); // 8진법 변환
System.out.println(Integer.toHexString(number)); // 16진법 변환
}
public static void conversion(int number, int N){
StringBuilder sb = new StringBuilder();
int current = number;
// 진법 변환할 숫자가 0보다 큰 경우 지속 진행
while(current > 0){
// 만약 N으로 나누었는데 10보다 작다면 해당 숫자를 바로 append
if(current % N < 10){
sb.append(current % N);
// 만약 N이 10보다 큰 경우, N으로 나누었는데 10 이상이면 A, B등으로 표현하므로 기존 숫자는 10진법이므로 10만큼 빼고 'A'를 더한다.
// 왜냐면 1~9까지는 숫자로 표기하지만, 10 부터는 'A', 'B' 순서로 나타내기 때문이다.
// 나머지가 10이라면 'A' + 10이 아니라 'A'로 나타내야 하기 때문
} else {
sb.append((char)(current % N - 10 + 'A'));
}
current /= N;
}
// StringBuilder의 reverse를 사용해야 정상적으로 출력 가능. 안그러면 거꾸로 출력됨
System.out.println("숫자 : " + number + "를 " + N + "진법으로 변환한 수 : " + sb.reverse());
}
}N진법에서 10진법으로 변환하기
수학적으로 이용하여 N진법의 각 숫자에 N을 곱해가면서 10진법으로 다시 바꾸면 된다. 아래의 코드를 통해 알아보자.
public class Main {
public static void main(String[] args) {
// String 형태로 해서 전달함. 7F등 10진법 이상에서는 A~Z의 문자를 사용하기 때문
// 전체 숫자를 다시 원래 숫자 127로 변환!
converse_ten("1111111", 2);
converse_ten("11201", 3);
converse_ten("1333", 4);
converse_ten("1002", 5);
converse_ten("177", 8);
converse_ten("7F", 16);
// 쉽게 진행하는 법 - 자바 내부에서 제공하는 방법 사용
// Integer.parseInt 진행 시, 숫자와 진법을 제공하면 10진법으로 쓰여진다.
System.out.println(Integer.parseInt("7F", 16));
}
public static void converse_ten(String number, int N){
char[] nums = number.toCharArray(); // char의 배열로 만들어서 하나씩 숫자별로 대응
int ans = 0; // 시작은 0으로 시작
// 아래에서 ans를 0으로 시작하고 계속 N(기존 진법)을 곱하고 있다.
// 이는, 앞자리의 숫자는 전체 m자리라면 m-1승 까지 곱해야 하기 때문
// 1의 자리는 0승 곱하면 되기 때문에 0으로 시작하는 것임
for(int i=0; i < nums.length; i++){ //??????
// 'A'이상의 숫자, 즉 10이상의 경우에는 'A'를 빼고 10을 더하면 원래 숫자가 됨
if(nums[i] >= 'A'){
ans = ans * N + (nums[i] - 'A' + 10);
// 그 이하는 단순히 '0'만 빼면 된다.
} else {
ans = ans * N + (nums[i] - '0');
}
}
System.out.println(ans);
}
}위의 코드를 이용해서 A - B 진법으로의 변환도 가능하다. 10진법을 중간에 끼워서 상호 변환 시키는 과정이나, 위의 코드를 기반으로 쉽게 해결할 수 있다.
2진법 - 16진법 변환하기
위에서 A - B 진법으로 변환은 10진법을 중간에 끼워서 코드를 동작시키면 된다고 했는데,
여기서는 2진법과 16진법을 상호 변환하는 방법을 알아보자.
2진법 - 16진법은 실제로 많이 쓰이는 경우가 많다
2진법 → 16진법
2진법의 숫자 4개를 이용 시, 0~15까지의 숫자를 나타낼 수 있다.
그렇다면, 16진법은 0~15까지를 하나의 숫자 혹은 문자로 나타내는 방법이므로 2진법의 숫자 4개씩 잘라서 변환을 시키면 된다. 아래의 표를 보자.(아래와 같이 변환 가능)
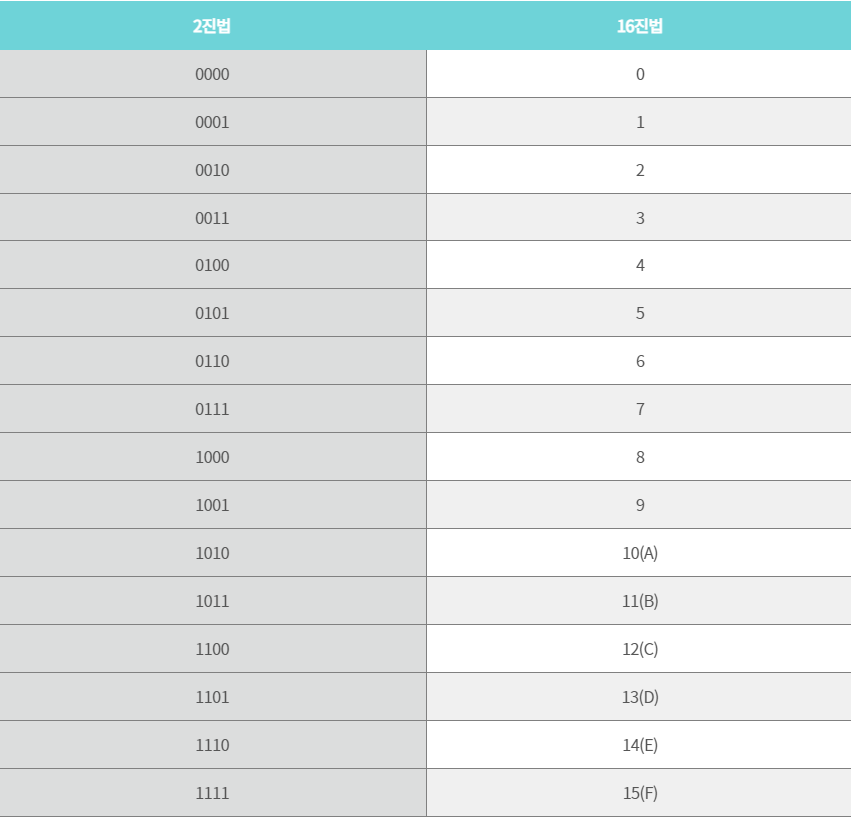
그렇다면, 1000 1100 은 16진법으로 어떻게 변환될까? 바로 8C 임을 알 수 있다.
주의할 점은, 2진법의 숫자가 10 1100 이면 4개로 정확히 끊어지지 않는다는 점이다. 이럴 때는, 앞에 00을 붙여 4개로 끊어지도록 만듦으로써 문제를 쉽게 해결할 수 있다.
코드를 통해 어떻게 변환이 되는지 알아보자.
public class Main {
public static void main(String[] args) {
System.out.println(bin2Hex("1101")); // 0xD
System.out.println(bin2Hex("100110")); // 0x26
System.out.println(bin2Hex("10010")); // 0x12
System.out.println(bin2Hex("111011")); // 0x3B
}
// 2진법 16진법으로 변환하는 method
public static String bin2Hex(String binary){
// 4자리씩 끊을 수 있도록 맞추어 준다.
StringBuilder add = new StringBuilder();
if(binary.length() % 4 != 0){
for(int i=0; i < 4 - binary.length() % 4; i++){
add.append("0");
}
}
String bin = add.toString() + binary; // 4자리씩 끊기는 2진법 수
StringBuilder hex = new StringBuilder(); // 16진법 변환 결과 값
// 4개 글자씩 끊어서 2진법 -> 16진법 변환 수행
for(int i=0; i < bin.length() / 4; i++){
String sub = bin.substring(i*4, i*4+4); // 4개 글자로 끊는다.
int sum = 0; // 10진수로 더해서 어떤 값인지 확인
for(int j=0; j< sub.length(); j++){
sum += (sub.charAt(j) - '0') * (int)Math.pow(2, 4-1-j);
}
if(sum > 9) hex.append((char)(sum - 10 + 'A')); // 10 이상이면 문자로 변환
else hex.append(sum); // 10미만이면 숫자 바로 적용
}
// 16진수임을 표시하기 위해 앞에 0x를 붙임.
return "0x" + hex.toString();
}
}