비트마스크
컴퓨터는 내부적으로 모든 자료를 이진수로 표현한다.
이와 같은 특성을 이용해 정수의 이진수 표현을 자료구조로 쓰는 기법을 비트마스크라고 한다.
장점
- 더 빠른 수행시간
- 더 간결한 코드
- 더 적은 메모리 사용
주의할점
시프트연산시 타입의 범위를 넘어가는 overflow, underflow를 매우 주의해야한다!
비트 연산자
a&b
a의 모든 비트와 b의 모든 비트를 AND연산한다.
둘 다 1이라면 1, 아니면 0을 반환
예)
a = 4 = 100(2)
b = 7 = 111(2)
a&b = 100(2) = 4
a|b
a의 모든 비트와 b의 모든 비트를 OR연산한다.
둘 다 0이라면 0, 아니면 1
예)
a = 2 = 010(2)
b = 5 = 101(2)
a|b = 111(2) = 7
a^b
a의 모든 비트와 b의 모든 비트를 XOR연산한다.
둘이 다르면 1, 같으면 0
예)
a = 3 = 011(2)
b = 5 = 101(2)
a|b = 110(2) = 6
~a
a의 모든 비트에 NOT연산을 한다
0이면 1, 1이면 0
예)3비트라고 가정
a = 3 = 011(2)
~a = 100(2) = 4
a<< b
a를 b만큼 왼쪽으로 시프트
예)
a = 1 = 011(2)
a<<2 = 100(2) = 4
a >> b
a를 b만큼 오른쪽으로 시프트
예)
a = 4 = 100(2)
a >> 2 = 011(2) = 1
집합의 표현
비트마스크를 이용해 집합을 쉽게 표현할 수 있다.
또 집합에 원소를 추가, 삭제하는 등 다양한 연산을 굉장히 빠르게 수행할 수 있다.
원소 개수가 N인 집합이 있다고 하면, 각 원소를 0~N-1번까지 번호를 부여하고, 번호에 해당하는 비트가 1이면 원소가 포함, 0이면 원소불포함이라고해서 집합을 비트를 이용해 표현할 수 있다.
예)
{A,B,C,D}라는 집합이 있다고 가정하자
예를 들어 {A,B}의 부분집합은 1000(2)=8로 표현하고, {C}의 부분집합은 0010(2) = 2 로 표현가능하다.
원소 추가
현재 상태 cur이 있을때 p번 원소를 추가한다고 가정하자.
그럼 현재 상태 cur에서 p번 비트를 1로 바꿔야한다.
이는 a|b 비트 연산을 이용하면 쉽게 해결가능하다.
cur = cur | (1<<p)
1<<p를 통해 p번 비트만 1, 나머지 비트는 0인 값을 만들고 '|'연산을 진행하면 cur의 p번 비트는 1로 바뀌며, 나머지 비트는 언래 상태를 유지한다.
원소 삭제
현재 상태 cur이 있을때 p번 원소를 삭제한다고 가정하자.
그럼 현재 상태 cur에서 p번 비트를 0으로 바꿔야한다.
cur = cur & ~(1<<p)
1<<p 를 통해 p번 비트만 1, 나머지 비트는 0으로 만든 후 '~'연산을 통해 p번 비트만 0, 나머지 비트는 1로 만든다
이후 '&'연산을 진행하면 p번 비트만 0으로 바뀌고 나머지는 현재상태 cur과 동일하게 유지할 수 있다
원소 토글
p번 비트가 1이면 0, 0이면 1로 바꾸는 토글 연산도 쉽게 구현가능하다.
현재 상태 cur에서 p번 원소가 있다면 삭제하고, 없으면 추가한다.
cur = cur^(1<<p)
XOR연산을 진행한다.
집합 연산(합집합)
합집합, 교집합, 차집합 등등 쉽게 구할 수 있다.
a|b; //a와 b의 합집합
a&b //a와 b의 교집합
a&~b //a에서 b를 뺀 차집합
a^b //a와 b중 하나에만 포함된 원소들의 집합 a&~b 연산을 하면 a 집합과 b의 여집합과 '&'연산을 한다. 따라서 A-B인 차집합이 연산된다
집합의 크기 구하기
현재 1로 켜져있는 비트의 수를 count해야한다.
따라서 모든 비트를 순회해야되며 재귀적으로 다음과같이 구현가능하다.
int bitCount(int x) {
if(x==0) return 0;
return x%2 + bitCount(x/2);
}x%2를 하면 마지막 비트를 얻게되고, x/2를 하면 마지막 비트를 삭제할 수 있다.
따라서 모든 비트를 재귀적으로 순회할 수 있다.
모든 부분 집합 순회하기
for (int subset = set ; subset ; subset = ((subset - 1) & set)){
//subset은 set의 부분집합 중 하나
}예를 들어 {A,B,D}를 포함한 집합을 생각해보자
모든 부분 집합은 공집합을 제외하고 {A}, {B},{D},{A,B},{A,D},{B,D},{A,B,D}가 존재한다.
이를 비트로표현하면 다음과같다.
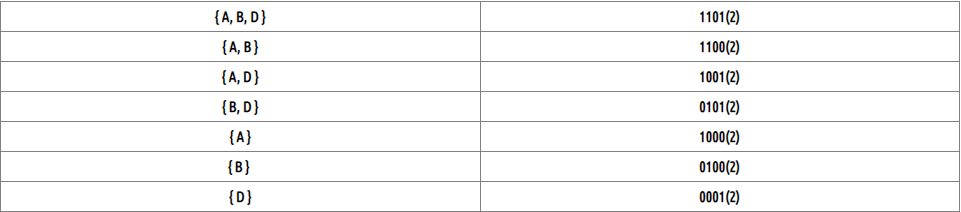
위에서 구현한 코드를 따라가보자.
set = 1101(2) = {A,B,D}이다.

for문을 통해 모든 부분 집합을 다 순회하는것을 확인할 수 있다.
