https://www.acmicpc.net/problem/12100
문제
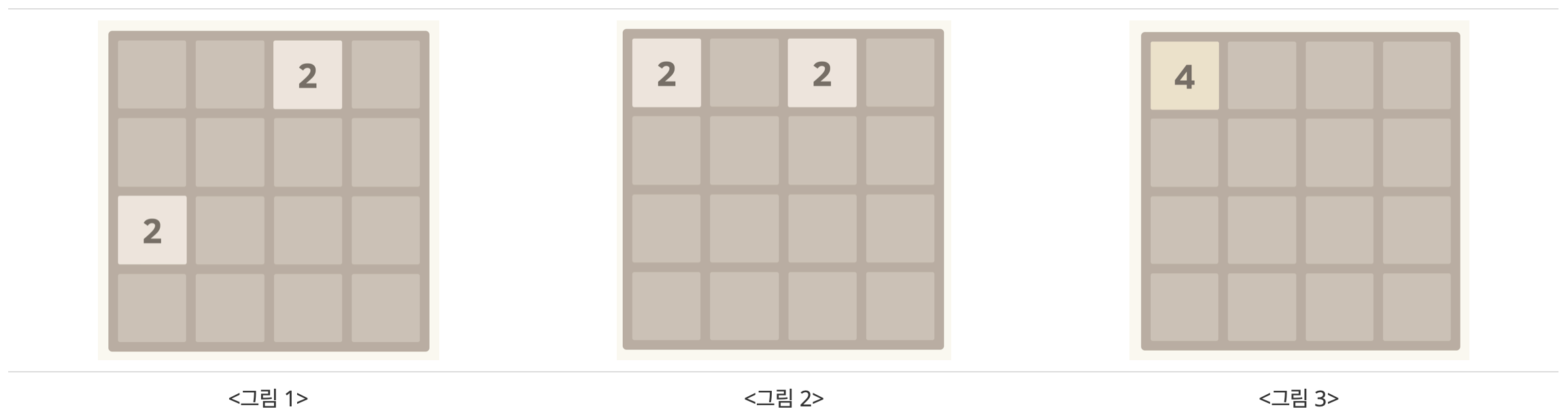
2048 게임은 4×4 크기의 보드에서 혼자 즐기는 재미있는 게임이다. 이 링크를 누르면 게임을 해볼 수 있다. 이 게임에서 한 번의 이동은 보드 위에 있는 전체 블록을 상하좌우 네 방향 중 하나로 이동시키는 것이다. 이때, 같은 값을 갖는 두 블록이 충돌하면 두 블록은 하나로 합쳐지게 된다. 한 번의 이동에서 이미 합쳐진 블록은 또 다른 블록과 다시 합쳐질 수 없다. (실제 게임에서는 이동을 한 번 할 때마다 블록이 추가되지만, 이 문제에서 블록이 추가되는 경우는 없다)
<그림 1>의 경우에서 위로 블록을 이동시키면 <그림 2>의 상태가 된다. 여기서, 왼쪽으로 블록을 이동시키면 <그림 3>의 상태가 된다.
<그림 4>의 상태에서 블록을 오른쪽으로 이동시키면 <그림 5>가 되고, 여기서 다시 위로 블록을 이동시키면 <그림 6>이 된다. 여기서 오른쪽으로 블록을 이동시켜 <그림 7>을 만들 수 있다.
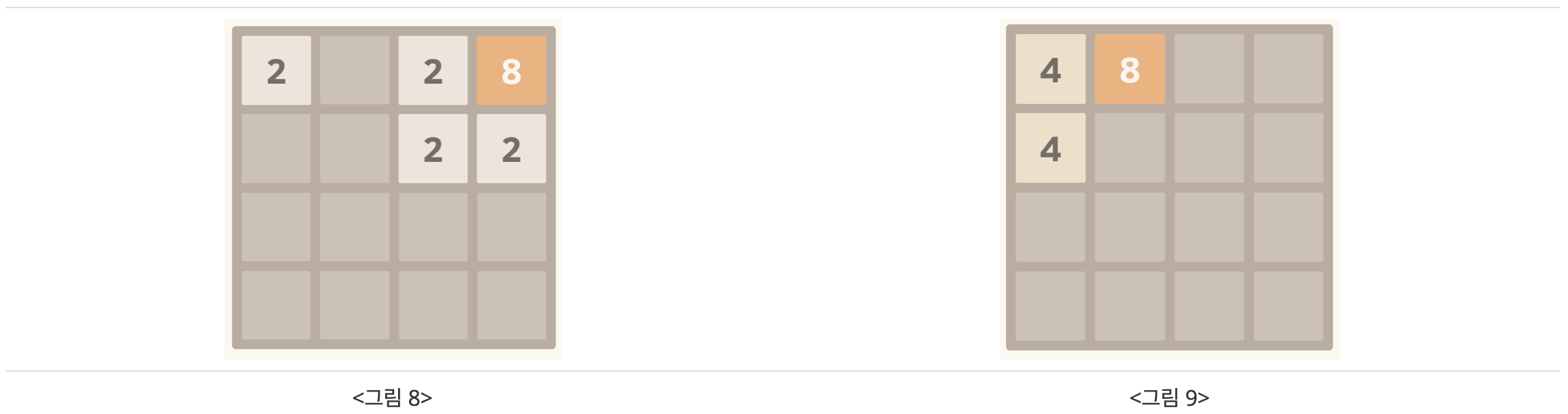
<그림 8>의 상태에서 왼쪽으로 블록을 옮기면 어떻게 될까? 2가 충돌하기 때문에, 4로 합쳐지게 되고 <그림 9>의 상태가 된다.
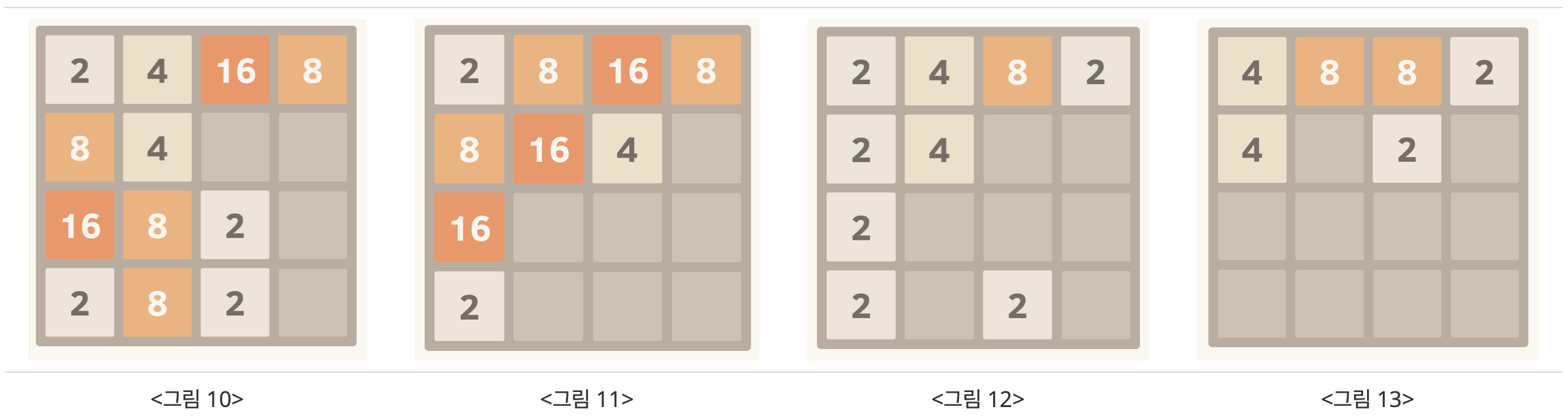
<그림 10>에서 위로 블록을 이동시키면 <그림 11>의 상태가 된다. <그림 12>의 경우에 위로 블록을 이동시키면 <그림 13>의 상태가 되는데, 그 이유는 한 번의 이동에서 이미 합쳐진 블록은 또 합쳐질 수 없기 때문이다.
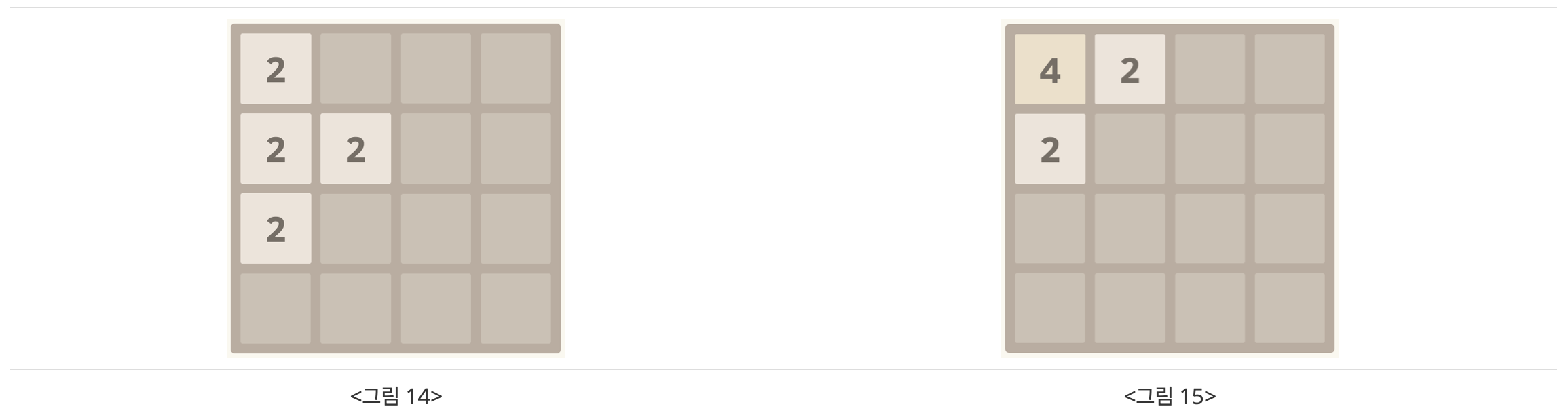
마지막으로, 똑같은 수가 세 개가 있는 경우에는 이동하려고 하는 쪽의 칸이 먼저 합쳐진다. 예를 들어, 위로 이동시키는 경우에는 위쪽에 있는 블록이 먼저 합쳐지게 된다. <그림 14>의 경우에 위로 이동하면 <그림 15>를 만든다.
이 문제에서 다루는 2048 게임은 보드의 크기가 N×N 이다. 보드의 크기와 보드판의 블록 상태가 주어졌을 때, 최대 5번 이동해서 만들 수 있는 가장 큰 블록의 값을 구하는 프로그램을 작성하시오.
입력 1
3
2 2 2
4 4 4
8 8 8
출력 1
16
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
int N;
int board[6][20][20];
bool visit[20][20] = {false,};
int maxval = 0;
bool flag;
void init(int x) {
memcpy(board[x], board[x - 1], sizeof(board[0]));
for(int i = 0; i < N; i++) {
for(int j = 0; j < N; j++) {
visit[i][j] = false;
}
}
}
void y_visit(int y, int z, int w) {
visit[y][w] = false;
visit[z][w] = true;
}
void x_visit(int y, int z, int w) {
visit[w][y] = false;
visit[w][z] = true;
}
int move(int x, int dir) {
flag = false;
init(x);
switch(dir) {
case 0:
for(int i = N - 2; i >= 0; i--) {
for(int j = 0; j < N; j++) {
if(board[x][i + 1][j] > 0 && board[x][i][j] == 0) {
board[x][i][j] = board[x][i + 1][j];
if(visit[i + 1][j])
y_visit(i + 1, i, j);
flag = true;
for(int k = i + 1; k < N - 1; k++) {
board[x][k][j] = board[x][k + 1][j];
visit[k][j] = visit[k + 1][j];
}
board[x][N - 1][j] = 0;
visit[N - 1][j] = false;
}
}
}
for(int i = 0; i < N - 1; i++) {
for(int j = 0; j < N; j++) {
if(board[x][i + 1][j] > 0) {
if((board[x][i + 1][j] == board[x][i][j]) && !visit[i + 1][j] && !visit[i][j]) {
board[x][i][j] = board[x][i + 1][j] + board[x][i][j];
maxval = max(maxval, board[x][i][j]);
y_visit(i + 1, i, j);
flag = true;
for(int k = i + 1; k < N - 1; k++) {
board[x][k][j] = board[x][k + 1][j];
visit[k][j] = visit[k + 1][j];
}
board[x][N - 1][j] = 0;
visit[N - 1][j] = false;
}
}
}
}
break;
case 1:
for(int i = 1; i < N; i++) {
for(int j = 0; j < N; j++) {
if(board[x][i - 1][j] > 0 && board[x][i][j] == 0) {
board[x][i][j] = board[x][i - 1][j];
if(visit[i - 1][j])
y_visit(i - 1, i, j);
flag = true;
for(int k = i - 1; k > 0; k--) {
board[x][k][j] = board[x][k - 1][j];
visit[k][j] = visit[k - 1][j];
}
board[x][0][j] = 0;
visit[0][j] = false;
}
}
}
for(int i = N - 1; i > 0; i--) {
for(int j = 0; j < N; j++) {
if(board[x][i - 1][j] > 0) {
if((board[x][i - 1][j] == board[x][i][j]) && !visit[i - 1][j] && !visit[i][j]) {
board[x][i][j] = board[x][i - 1][j] + board[x][i][j];
maxval = max(maxval, board[x][i][j]);
y_visit(i - 1, i, j);
flag = true;
for(int k = i - 1; k > 0; k--) {
board[x][k][j] = board[x][k - 1][j];
visit[k][j] = visit[k - 1][j];
}
board[x][0][j] = 0;
visit[0][j] = false;
}
}
}
}
break;
case 2:
for(int j = N - 2; j >= 0; j--) {
for(int i = 0; i < N; i++) {
if(board[x][i][j + 1] > 0 && board[x][i][j] == 0) {
board[x][i][j] = board[x][i][j + 1];
if(visit[i][j + 1])
x_visit(j + 1, j, i);
flag = true;
for(int k = j + 1; k < N - 1; k++) {
board[x][i][k] = board[x][i][k + 1];
visit[i][k] = visit[i][k + 1];
}
board[x][i][N - 1] = 0;
visit[i][N - 1] = false;
}
}
}
for(int j = 0; j < N - 1; j++) {
for(int i = 0; i < N; i++) {
if(board[x][i][j + 1] > 0) {
if((board[x][i][j + 1] == board[x][i][j]) && !visit[i][j + 1] && !visit[i][j]) {
board[x][i][j] = board[x][i][j + 1] + board[x][i][j];
maxval = max(maxval, board[x][i][j]);
x_visit(j + 1, j, i);
flag = true;
for(int k = j + 1; k < N - 1; k++) {
board[x][i][k] = board[x][i][k + 1];
visit[i][k] = visit[i][k + 1];
}
board[x][i][N - 1] = 0;
visit[i][N - 1] = false;
}
}
}
}
break;
case 3:
for(int j = 1; j < N; j++) {
for(int i = 0; i < N; i++) {
if(board[x][i][j - 1] > 0 && board[x][i][j] == 0) {
board[x][i][j] = board[x][i][j - 1];
if(visit[i][j - 1])
x_visit(j - 1, j, i);
flag = true;
for(int k = j - 1; k > 0; k--) {
board[x][i][k] = board[x][i][k - 1];
visit[i][k] = visit[i][k - 1];
}
board[x][i][0] = 0;
visit[i][0] = false;
}
}
}
for(int j = N - 1; j > 0; j--) {
for(int i = 0; i < N; i++) {
if(board[x][i][j - 1] > 0) {
if((board[x][i][j - 1] == board[x][i][j]) && !visit[i][j - 1] && !visit[i][j]) {
board[x][i][j] = board[x][i][j - 1] + board[x][i][j];
maxval = max(maxval, board[x][i][j]);
x_visit(j - 1, j, i);
flag = true;
for(int k = j - 1; k > 0; k--) {
board[x][i][k] = board[x][i][k - 1];
visit[i][k] = visit[i][k - 1];
}
board[x][i][0] = 0;
visit[i][0] = false;
}
}
}
}
break;
}
return flag;
}
void num(int x) {
if(x == 6)
return;
for(int dir = 0; dir < 4; dir++) {
if(!move(x, dir))
continue;
num(x + 1);
}
}
int main() {
scanf("%d", &N);
for(int i = 0; i < N; i++) {
for(int j = 0; j < N; j++) {
scanf("%d", &board[0][i][j]);
maxval = max(maxval, board[0][i][j]);
}
}
num(1);
printf("%d\n", maxval);
}최대 5번 이동할 수 있으므로 재귀함수를 사용해서 이동 횟수를 증가시킨다.
4가지 방향을 방향 1, 2, 3, 4라고 부르자. K(0 < K < 6)번째 이동에서 방향 0로 이동했을 때 블록의 변화가 있다면, 다음 재귀 함수를 불러 K + 1(0 < K < 6)번째 이동에서 방향 0으로 이동한다. 만약 블록의 변화가 없으면 방향 1으로 이동한다.
블록이 이동하는 경우는 두 가지가 있다. 블록이 비어 있어 이동할 수 있는 경우와 이동하는 방향으로 같은 숫자가 있으면 합쳐지는 경우다. 단, 후자의 경우 위 <그림 14>의 조건과 한 번의 이동에서 이미 합쳐진 블록은 다시 합쳐질 수 없음을 명심해야 한다. 나는 두 가지 경우를 따로 계산했다. switch 문의 조건은 방향을 나타내는데 각 방향마다 이중 반복문이 두개가 있다. 첫번째는 블록이 비어 있어 이동하는 경우고 두번째는 같은 숫자가 있으면 합쳐지는 경우다. 그리고 블록이 합쳐질 때마다 maxval 값과 계속 비교하면 가장 큰 블록을 구할 수 있다.
4시간 정도 걸렸다.. 코드가 더럽지만 오늘은 그만하고 싶어서 그냥 올렸다. Easy 버전도 나한테는 어려웠지만.. Hard 버전도 다음에 풀어봐야지😐