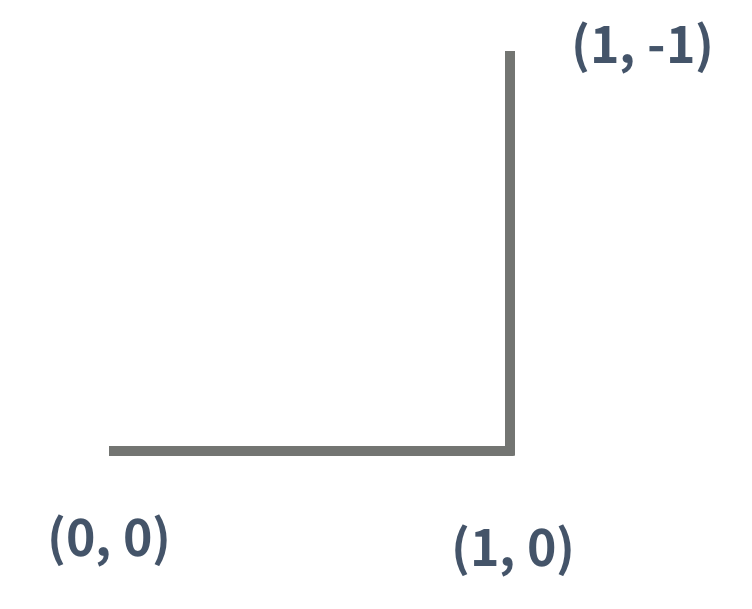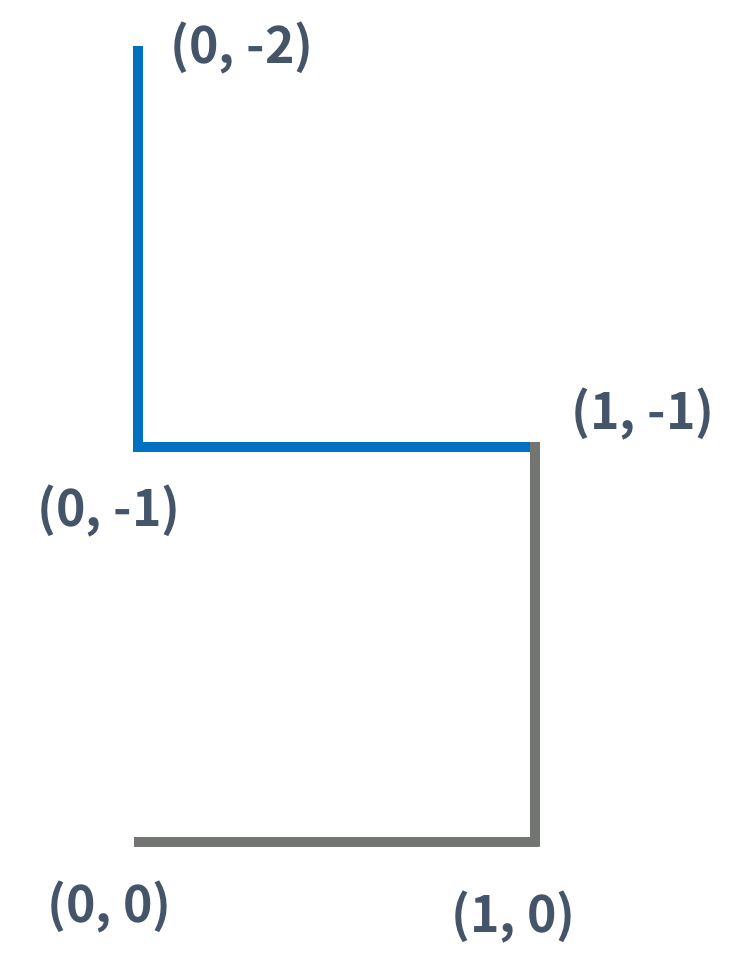[BOJ] 15685번 드래곤 커브 c++

https://www.acmicpc.net/problem/15685

문제
드래곤 커브는 다음과 같은 세 가지 속성으로 이루어져 있으며, 이차원 좌표 평면 위에서 정의된다. 좌표 평면의 x축은 → 방향, y축은 ↓ 방향이다.
1. 시작 점
2. 시작 방향
3. 세대
0세대 드래곤 커브는 아래 그림과 같은 길이가 1인 선분이다. 아래 그림은 (0, 0)에서 시작하고, 시작 방향은 오른쪽인 0세대 드래곤 커브이다.

1세대 드래곤 커브는 0세대 드래곤 커브를 끝 점을 기준으로 시계 방향으로 90도 회전시킨 다음 0세대 드래곤 커브의 끝 점에 붙인 것이다. 끝 점이란 시작 점에서 선분을 타고 이동했을 때, 가장 먼 거리에 있는 점을 의미한다.

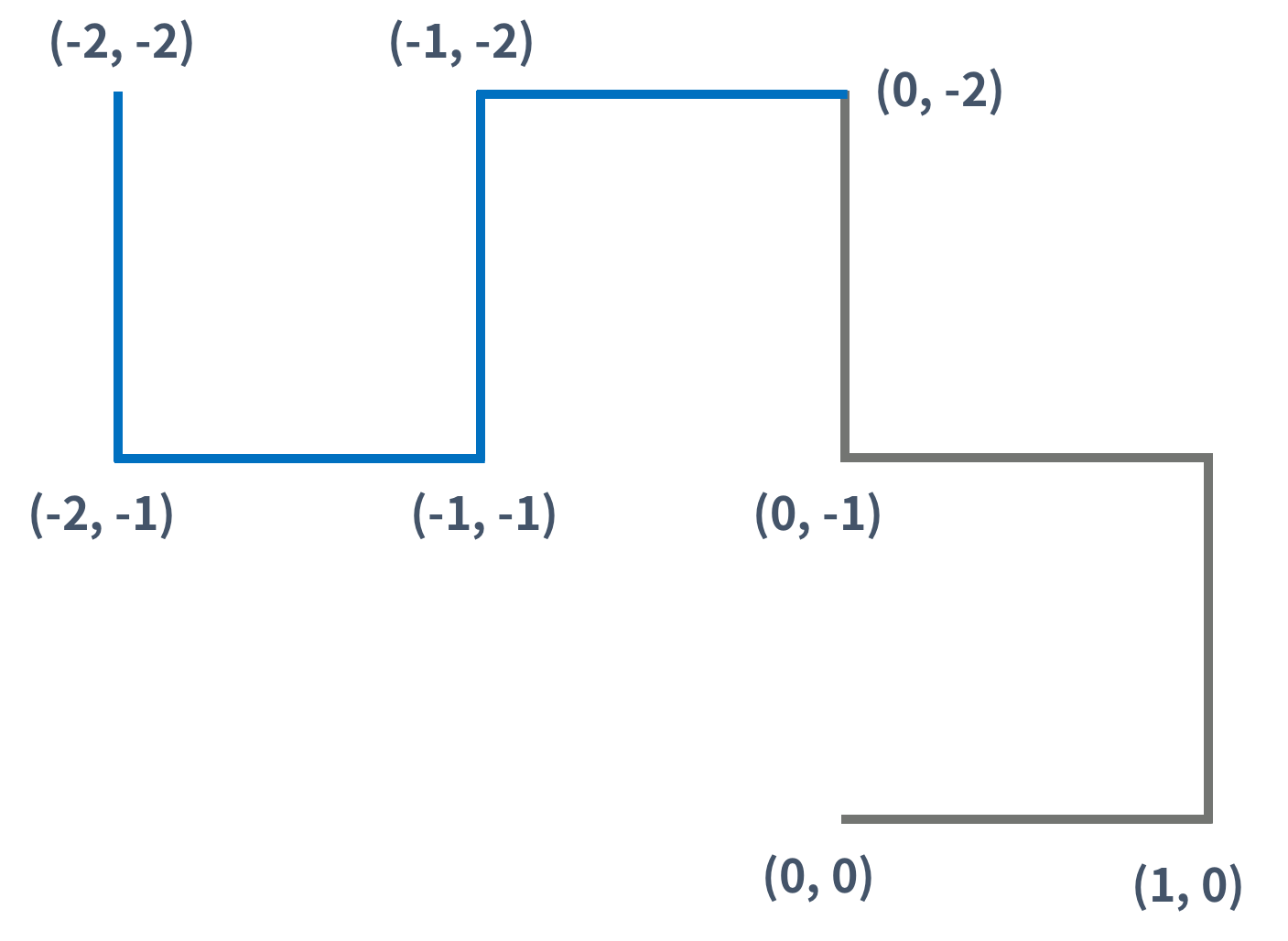
2세대 드래곤 커브도 1세대를 만든 방법을 이용해서 만들 수 있다. (파란색 선분은 새로 추가된 선분을 나타낸다)

3세대 드래곤 커브도 2세대 드래곤 커브를 이용해 만들 수 있다. 아래 그림은 3세대 드래곤 커브이다.

즉, K(K > 1)세대 드래곤 커브는 K-1세대 드래곤 커브를 끝 점을 기준으로 90도 시계 방향 회전 시킨 다음, 그것을 끝 점에 붙인 것이다.
크기가 100×100인 격자 위에 드래곤 커브가 N개 있다. 이때, 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 정사각형의 개수를 구하는 프로그램을 작성하시오. 격자의 좌표는 (x, y)로 나타내며, 0 ≤ x ≤ 100, 0 ≤ y ≤ 100만 유효한 좌표이다.

---

입력 1
3
3 3 0 1
4 2 1 3
4 2 2 1

출력 1
4

---

입력 2
4
3 3 0 1
4 2 1 3
4 2 2 1
2 7 3 4

출력 2
11

---

입력 3
10
5 5 0 0
5 6 0 0
5 7 0 0
5 8 0 0
5 9 0 0
6 5 0 0
6 6 0 0
6 7 0 0
6 8 0 0
6 9 0 0

출력 3
8

---

입력 4
4
50 50 0 10
50 50 1 10
50 50 2 10
50 50 3 10

출력 4
1992

---

#include <iostream>
#include <cstdio>
#include <stack>

using namespace std;

int dy[4] = {0, -1, 0, 1};
int dx[4] = {1, 0, -1, 0};

int N;
int x, y, d, g;
int arr[101][101] = {0,};

void draw() {
  stack<int> s, tmp;
  int ny, nx, nd;

  // generation 0
  arr[y][x] = 1;
  ny = y + dy[d];
  nx = x + dx[d];

  if(-1 < ny && ny < 101 && -1 < nx && nx < 101)
    arr[ny][nx] = 1;
  y = ny;
  x = nx;

  s.push(d);

  for(int i = 1; i <= g; i++) {
    tmp = s;
    while(!tmp.empty()) {
      d = tmp.top();
      tmp.pop();

      nd = (d + 1) < 4 ? d + 1 : 0;
      ny = y + dy[nd];
      nx = x + dx[nd];

      if(-1 < ny && ny < 101 && -1 < nx && nx < 101)
        arr[ny][nx] = 1;
      y = ny;
      x = nx;

      s.push(nd);
    }
  }
}

int main() {
  int cnt = 0;
  scanf("%d", &N);
  for(int i = 0; i < N; i++) {
    scanf("%d %d %d %d", &x, &y, &d, &g);
    draw();
  }

  for(int i = 0; i < 100; i++) {
    for(int j = 0; j < 100; j++) {
      if(arr[i][j] && arr[i][j + 1] && arr[i + 1][j] && arr[i + 1][j + 1])
      cnt += 1;
    }
  }

  printf("%d\n", cnt);
}