| Type | Name | Rule | Recognizer |
|---|---|---|---|
| 0 | Recursively Enummerable Language | 아무런 제약이 없음 | Turing Machine |
| 1 | Context Sensitive Language | A -> B (|A| <= |B|) | Linear Bounded Automata |
| 2 | Context Free Language | A -> B (|A| <= |B|, |A| = 1) | Push-Down Automata |
| 3 | Regular Language | A -> tB, A -> t or A -> Bt, A -> t (|A| <= |B|, |A| = 1, t는 터미널, B는 논터미널) | Finite Automata |
Context Free Language
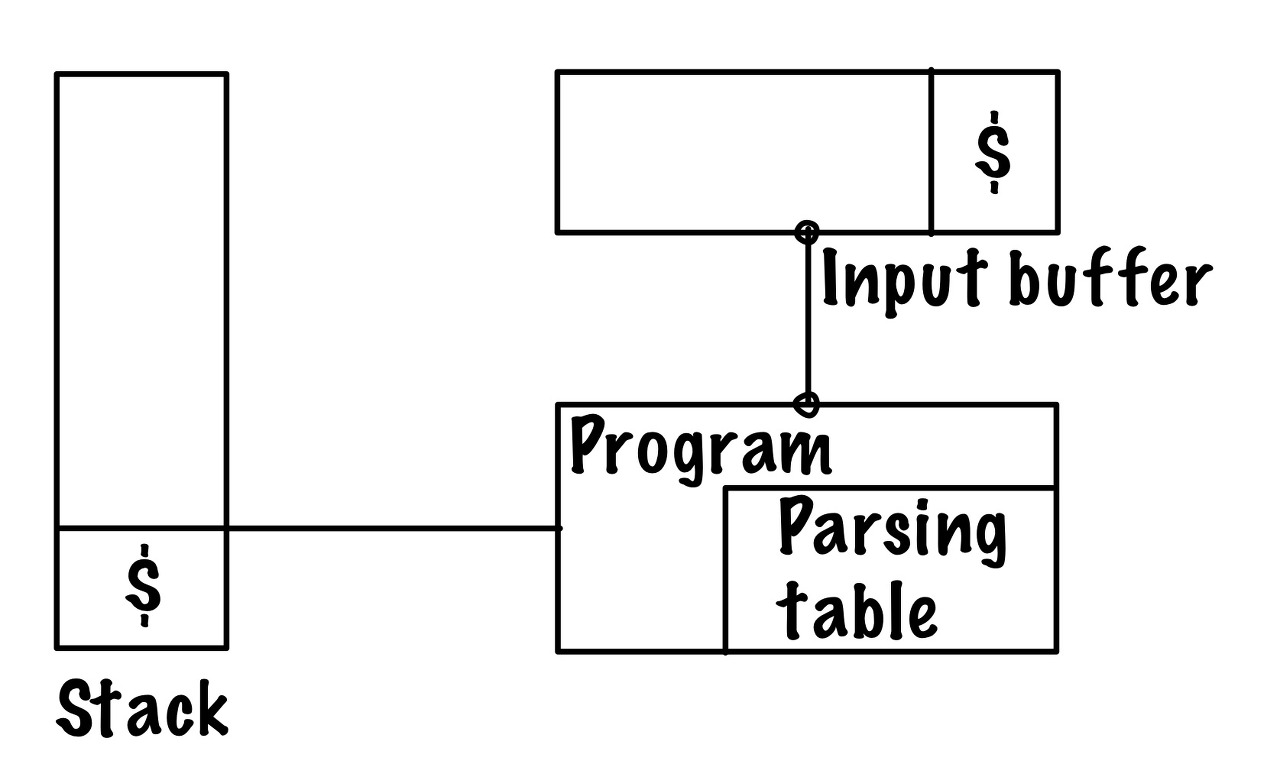
위 그림의 푸시 다운 오토마타(push-down-automata)는 입력 버퍼(input buffer)와 유한 상태 제어(finite state control)으로 구성된 유한 오토마타(finite automata)에 스택(stack)을 추가했다. 스택을 추가함으로써 이전의 상태로 돌아갈 수 있다. 푸시(push) 연산을 하면 새로운 상태로 전이(transition)되고, 팝(pop) 연산을 하면 이전의 상태로 돌아간다.
Regular Language
정규 언어(regular language)는 무한하다는 특성을 갖고 있지만 이를 인식하는 유한 오토마타는 유한한 메모리를 가지고 있다. 따라서 어느 단계에서나 문자열을 처리할 때 기억해야 할 정보가 제한되어야만 정규 언어라고 할 수 있다.
정규 언어가 아님을 보일 수 있는 방법이 펌핑 보조 정리를 사용하는 것이다. (펌핑 보조 정리를 만족한다고 해서 반드시 정규 언어인 것은 아니다.)
Pigeonhole princle에 따르면, m개의 상자에 n개의 물건을 넣는다면(n > m), 적어도 하나의 상자는 2개 이상의 물건을 가지고 있어야 한다.
언어 L = {a^n b^n : n >= 0}을 예로 들자.
유한 오토마타는 유한한 메모리, 즉 유한한 상태를 가지고 있다. 반면에 정규 언어는 무한하다. 두 특징을 종합하면, 똑같은 상태 q0에서 a^n, a^m(n != m)을 입력받았을 때 상태 q로 전이되는 경우가 있다. 그리고 유한 오토마타는 a^n b^n를 허락(accept)하므로 상태 q에서 b^n을 입력 받았을 때 final state로 가야만 한다. 하지만 상태 q0에서 a^m을 입력 받아 상태 q로 가고, q에서 b^n을 입력받아 final state로 간다.
정리해서 말하자면 n과 m이 같을 때에만 a^m b^n이 final state로 가야하지만 m과 n이 다르므로 모순이 생긴다. 오토마타가 a^m b^n을 허락하지 않아야 하지만 그러지 못한다는 것이다.
따라서 언어 L은 정규 언어라고 할 수 없다.