Camera Calibration and Image of Absolute Conic (IAC)

=> vanishing point와 vanishing line을 찾아서 calibration하는 법

$(d,0)^T$의 ray는 vanishing point를 가진다. $v = P(d,0)^T$

3차원에 있는 plane에 대해 알고 싶어서, 그 plane에 대한 vanishing line: $l$을 조사함

l을 조사하다도면, 3차원에 있는 plane의 normal vector를 구할 수 있다.

image plane 상의 vanishing point와 plane at infity상의 point는 homography = $KR$ 관계를 가진다.

absolute conic을 image plane으로 보내보면 $w = K^{-T}K^{-1}$임을 알 수 있는데, 여기서 $w$를 알고 있다면, $K$ 즉 camera의 내부 파라미터를 구할 수 있다. (by cheolesky factorization) $v = KRd$ 도 구할 수 있고, $d = (KR)^{-1}v$ 도 구할 수 있다.

3차원 공간상 2개의 ray의 각도를 구할 수 있다. (vanishing point를 먼저 구하면)

• $K$를 구하기위해 $w$를 구해야되고, $w$를 구하기 위해 임의의 두개 ray 사이의 각이 90인걸 이용한다.

직각인 서로 다른 2개의 plane의 법선 벡터을 이용할 수도 있다.

Fundamental Matrix

epipolar geometry: 다른 카메라에 대한 이미지 plane에 맺히는 같은 두 점 사이의 관계를 알고자 하는 geometry

Fundamental matrix 유도

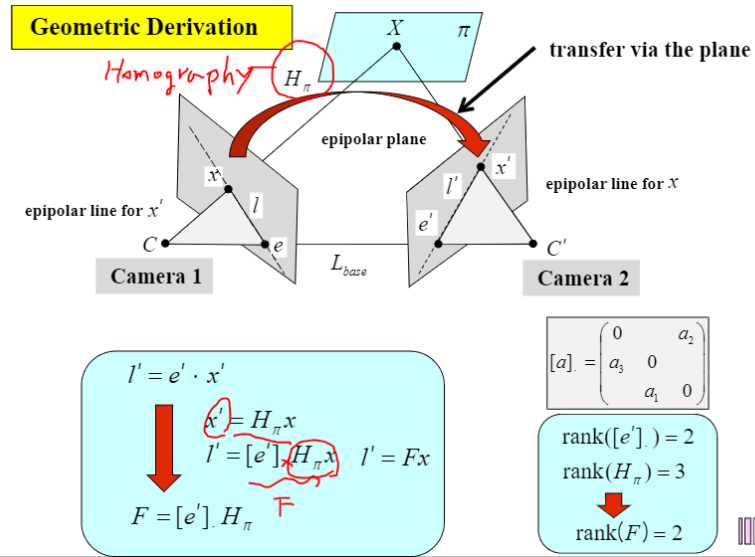
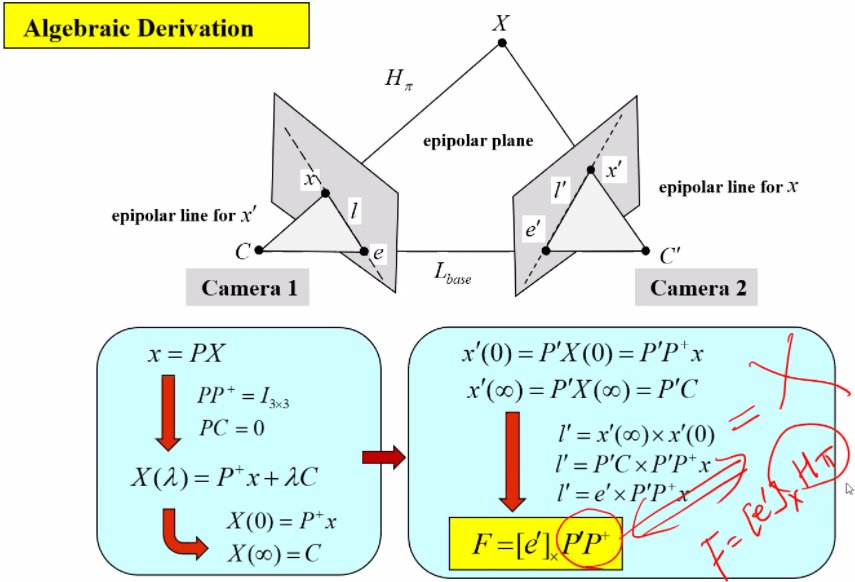
Epipolar constraint를 이용해서 F를 구하는 법 (대응점을 이용해서 homography를 구하는 것 처럼)

7개의 식으로 F를 구할 수 있다. + determinant가 0인 조건

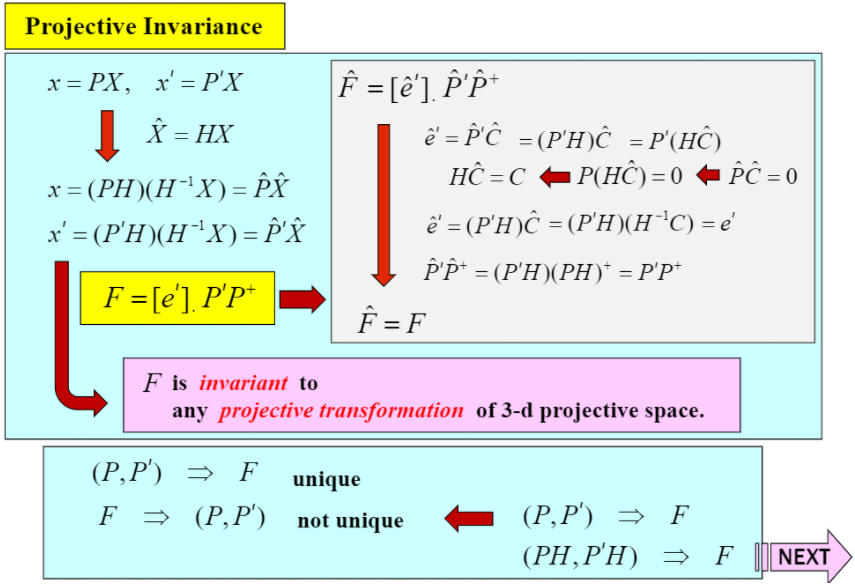
P의 쌍으로는 unique한 F를 구할 순 있지만, F로 부터 P의 쌍을 unique하게 구할 순 없다. (P, P'에 대해 Homography를 한 후에 F를 구한 값과 P, P'을 가지고 그대로 F를 구한 값과 같다.)

P와 P'을 이용하여 만든 F에 대해 위 행렬은 skew-symmetric이 된다.