MVG
1.Hello MVG!

I'm gonna write down the memo of study "Multiple View Geometry in computer vision".Having read the foreword of this book, this sentence was so interes
2.Homogenous Coordinate - 2D
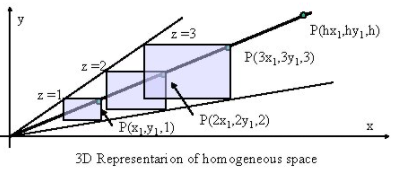
Before you read!This book has two notations,"Geometric Representation" and "Algebraic Representation". It would be confused of these combined notation
3.Conic (Proper & Degenerated Conic)
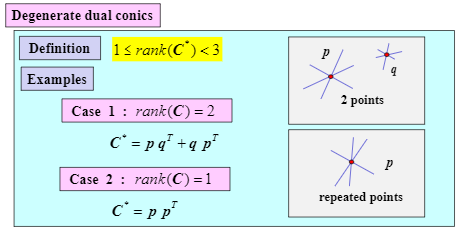
Conic can be represented by 6 parameters, $$ax^2 + bxy + cy^2 + dx + ey + f = 0$$it can also represented with matrix form like this:$\\begin{pmatrix}a
4.Projective Geometry - 2D: Homography
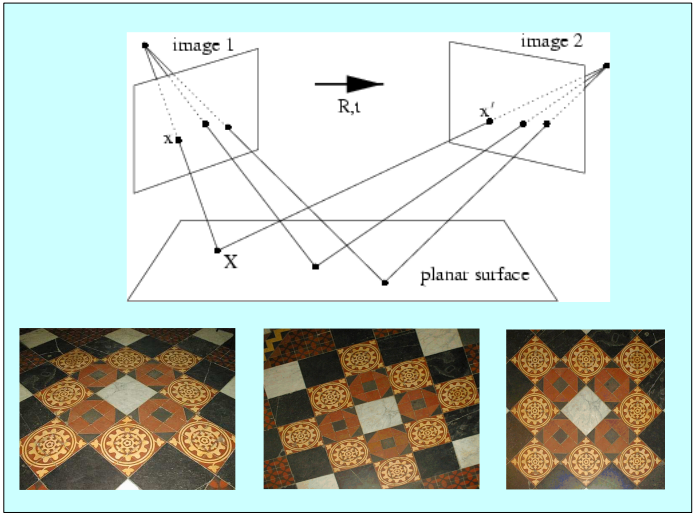
Definition : A mapping $h(.): P^2 => P^2$ such that $$x_1, x_2, x_3 \\ \\ \\ lie \\ on \\ the \\ same \\ line => h(x_1), h(x_2), h(x_3) $$Transformati
5.Rectification (Affine, Metric) with Vanishing Point

i) Taking two parallel lines and find the vanishing line.ii) Taking a vanishing line that is in a finite space into a line at infinity $(0,0,1)$iii) D
6.Camera coordinate & Distortion
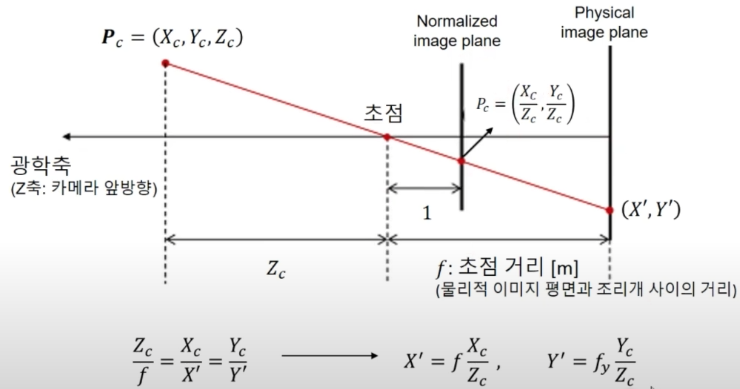
Here we're gonna learn how the point in the world coordinate is mapped to the point in the camera coordinate.Global steps1) World coordinate to camera
7.Direct Linear Transformation (DLT) Algorithm
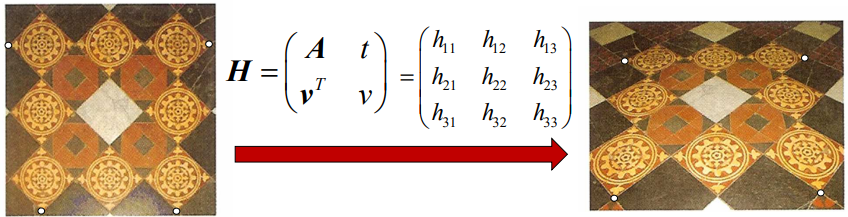
Given 2D to 2D point correspondences {$x_i <=> x'\_i$} Compute a 3x3 matrix $H$ such that$$ Hx_i = x'\_i \\ \\ for \\ all \\ i$$The Number of requi
8.Camera Calibration and Image of Absolute Conic (IAC)
=> vanishing point와 vanishing line을 찾아서 calibration하는 법$(d,0)^T$의 ray는 vanishing point를 가진다. $v = P(d,0)^T$3차원에 있는 plane에 대해 알고 싶어서, 그 plane에 대한 vanis