Homogenous Coordinate - 2D

Before you read!

This book has two notations,"Geometric Representation" and "Algebraic Representation". It would be confused of these combined notations. These two notations which means that points are same.

Notation of Points

$X : (x, y) \in \Re^2 : algebraic$

$X : (kx, ky, k) \in P^2 : Geometric$

The line can be written in same rule. when k is not zero.

Notation of Lines

$l : (kx, ky, k) \in P^2$

Q. What is the homogenous coordinates?

A. Homogenous coordinates is kind of coordinates such as "Cartesian coordinate", "Euclidean coordinate". The main difference from others is to use scale factor as a last component of vector.

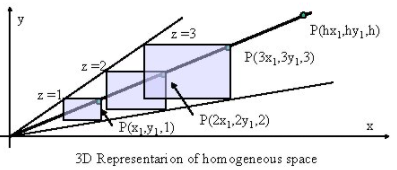
This book covered about "How does 3D Object been mapped from 2D space and vice versa. This representation, Homogenous coordinates", would be really useful tools to express them and know each relationships. And It can represent the point at infinity which is unfamiliar with the one who has ever heard about it.

Then what is the point at infinity? It can be represented by this definition.

$X : (x_1, x_2, x_3) \in \Re^2 : x_3 = 0 \ and \ \ x_1 \ne 0 \ \ and \ \ x_2 \ne 0$

Same as the word, the point at infinity (Ideal point) is located on infinity space. For example, There is a parellel lane on the ground and we know that the two lines do not meet each other. But, When we draw the extended line, it looks like they meet at the end of the line. we can find the point where two lines meet in the image, we can call it as point at infinity. Thinking of Parrellel lane of the train!

In next article, I would like to define some numerical expressions such as "Conic", "Dual Conic" and their relationships in the next post. These would be used to representing the relationships between point and line so it would be better to learn.

Thank you for your attention!