BFS (Breadth-First Search)

개념

BFS는 그래프 탐색 알고리즘 중 하나로, 시작 정점에서부터 인접한 정점들을 먼저 탐색하는 방법입니다. 너비 우선 탐색이라고도 불리며, 큐(Queue) 자료구조를 사용하여 구현됩니다. BFS는 정점들을 방문하는 순서대로 탐색하며, 같은 레벨에 있는 정점들을 먼저 탐색합니다.

너비우선탐색은 특히나 맹목적인 탐색을 하고자 할 때 사용할 수 있는 탐색 기법입니다. “최단경로”를 찾아준다는 점에서 최단길이를 보장해야 할 때 많이 사용합니다.

BFS는 탐색 방식 중 하나로 그 자체로는 큰 의미가 없고 여러 다른 알고리즘에서 BFS가 적용되어 효과적으로 사용되는데에 큰 의미가 있습니다.

BFS, DFS 방식 비교

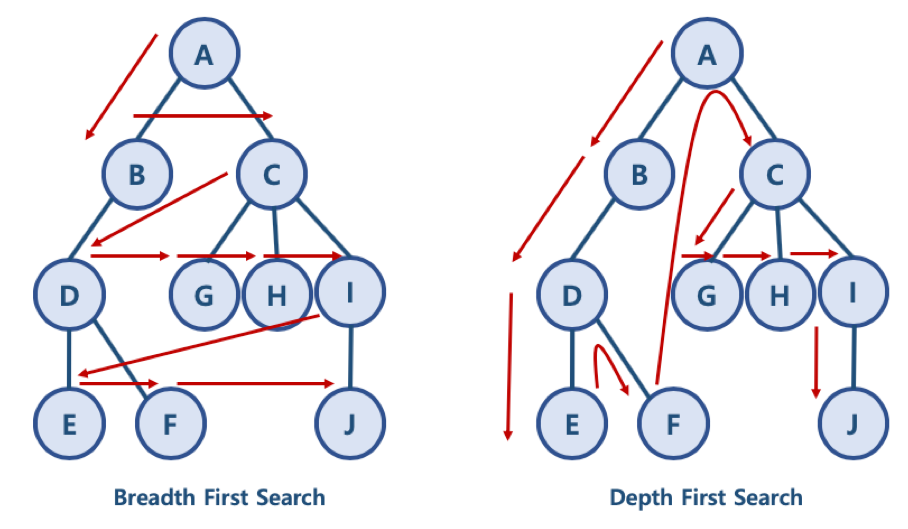
• BFS 방식: A - B - C - D - G - H - I - E - F - J
  • 한 단계씩 내려가면서, 해당 노드와 같은 레벨에 있는 노드들 (형제 노드들)을 먼저 순회함
• DFS 방식: A - B - D - E - F - C - G - H - I - J
  • 한 노드의 자식을 타고 끝까지 순회한 후, 다시 돌아와서 다른 형제들의 자식을 타고 내려가며 순화함

장점

• 최단 경로를 찾는 문제에 적합합니다.
• 최단 경로의 길이를 구하는 데 유용합니다.
• 모든 정점을 탐색하는데 유용합니다.

단점

• 그래프의 깊은 부분을 탐색하기 위해서는 많은 메모리가 필요할 수 있습니다.
• 방문한 정점들을 모두 저장해야 하므로 그래프가 매우 큰 경우 메모리 사용량이 증가할 수 있습니다.

사용에 적합한 상황

• 최단 경로를 찾는 문제 또는 모든 정점을 탐색해야 할 때 사용됩니다.
• 그래프의 깊이보다 너비가 중요한 문제에 적합합니다.

사용에 부적합한 상황

• 그래프의 깊은 부분을 우선적으로 탐색해야 하는 경우 BFS는 적합하지 않습니다.
• 메모리 사용량이 제한적인 경우에는 다른 탐색 알고리즘을 고려해야 합니다.

주의사항

• 방문한 정점을 반복해서 방문하지 않도록 체크해야 합니다.
• 큐에 정점을 중복해서 넣지 않도록 주의해야 합니다.
• 그래프에 순환 경로가 있는 경우 무한 루프에 빠질 수 있습니다.

시간 복잡도

• BFS는 그래프의 모든 정점과 간선을 방문하기 때문에 시간 복잡도는 O(V + E)입니다. 여기서 V는 정점의 수, E는 간선의 수를 의미합니다.

구현 코드

• Python

  graph = dict()
  
  graph['A'] = ['B', 'C']
  graph['B'] = ['A', 'D']
  graph['C'] = ['A', 'G', 'H', 'I']
  graph['D'] = ['B', 'E', 'F']
  graph['E'] = ['D']
  graph['F'] = ['D']
  graph['G'] = ['C']
  graph['H'] = ['C']
  graph['I'] = ['C', 'J']
  graph['J'] = ['I']
  
  def bfs(graph, start_node):
      visited = list()
      need_visit = list()
      
      need_visit.append(start_node)
      
      while need_visit:
          node = need_visit.pop(0)
          if node not in visited:
              visited.append(node)
              need_visit.extend(graph[node])
      
      return visited
  
  bfs(graph, 'A')

• JS

  function bfs(graph, start) {
    const visited = new Set();
    const queue = [start];
    visited.add(start);
  
    while (queue.length > 0) {
      const vertex = queue.shift();
      console.log(vertex);
  
      for (const neighbor of graph[vertex]) {
        if (!visited.has(neighbor)) {
          queue.push(neighbor);
          visited.add(neighbor);
        }
      }
    }
  }
  
  //   그래프
  //     A
  //    / \
  //   B   C
  //  /     \
  // D       E
  const graph = {
    A: ['B', 'C'],
    B: ['A', 'D'],
    C: ['A', 'E'],
    D: ['B'],
    E: ['C'],
  };
  
  // 시작 정점
  const start = 'A';
  
  // BFS 탐색 시작
  bfs(graph, start);

  function bfs(graph, start) {
    const queue = [start];
    const visited = new Set();
  
    while (queue.length) {
      const vertex = queue.shift();
  
      if (!visited.has(vertex)) {
        visited.add(vertex);
  
        for (const neighbor of graph[vertex]) {
          queue.push(neighbor);
        }
      }
    }
  
    return visited;
  }
  
  bfs(graph, 'A'); // ['A', 'B', 'D', 'C', 'E', 'F']

  Set은 자바스크립트의 내장 객체로, 중복된 값을 허용하지 않고 유일한 값만을 저장하는 자료구조입니다. Set은 순서가 보장되지 않으며, 주로 집합 연산이 필요한 경우 또는 중복을 제거하고 고유한 값만을 다루어야 할 때 사용됩니다.

  BFS에서 Set을 사용하는 이유는 방문한 정점들을 기록하기 위해서입니다. BFS 알고리즘은 정점을 방문할 때마다 해당 정점을 방문했음을 표시해야 합니다. Set을 사용하면 중복된 값을 허용하지 않기 때문에 이미 방문한 정점을 쉽게 체크할 수 있습니다. 이미 방문한 정점을 다시 큐에 넣지 않기 위해 Set을 사용합니다.

  배열을 사용하여 방문한 정점들을 기록하고, 탐색 대상인 정점들을 큐에 저장할 수도 있습니다. 그러나 배열은 중복된 값을 허용하기 때문에 중복 체크를 위해 추가적인 로직을 구현해야 합니다.

  Set을 사용하면 중복된 값을 허용하지 않기 때문에 이미 방문한 정점을 쉽게 체크할 수 있습니다. Set은 값의 유일성을 보장하며, 효율적인 중복 체크를 제공합니다. 이를 통해 중복된 정점을 제외하고 유일한 정점들을 기록하고, 탐색할 정점들을 큐에 저장하는데 더 간단하고 효율적인 방법을 제공합니다.