DFS (Depth-First search)

개념

깊이 우선 탐색(DFS, Depth-First Search)은 그래프에서 사용되는 탐색 알고리즘 중 하나입니다. 시작 정점에서부터 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방식으로 동작합니다. 즉, 가능한 한 깊숙히 들어가면서 노드를 탐색하고, 더 이상 탐색할 수 없을 때 backtracking하여 다음 분기로 넘어가는 방식입니다.

너비우선과는 다르게 queue가 아닌 stack을 사용합니다.

너비우선 탐색과 마찬가지로 맹목적인 탐색을 하고자 할 때 사용할 수 있으며, 깊이우선 탐색 그 자체로 큰 의미가 없고 다른 알고리즘에서 DFS가 작용되어 효과적으로 사용되는데에 큰 의미가 있습니다.

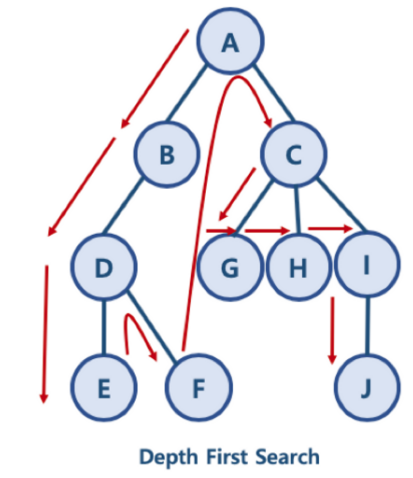
• DFS 방식: A - B - D - E - F - C - G - H - I - J
  • 한 노드의 자식을 타고 끝까지 순회한 후, 다시 돌아와서 다른 형제들의 자식을 타고 내려가며 순화함

장점

• 모든 경로를 탐색하므로 해답을 항상 찾을 수 있습니다.
• 메모리를 적게 사용하는 경향이 있습니다.
• 구현이 비교적 간단합니다.

단점

• 최단 경로를 찾는 문제에 적합하지 않을 수 있습니다.
• 무한루프에 빠질 가능성이 있습니다.
• 재귀 호출을 사용하여 구현할때는 스택 오버플로우가 발생할 수 있습니다.

사용에 적합한 상황

• 모든 경로를 탐색하고자 할 때
• 미로 탐색, 그래프 순회 등의 문제에서 사용할 수 있습니다.

사용에 부적합한 상황

• 최단 경로를 찾아야 할 때
• 그래프의 규모가 매우 큰 경우

주의사항

• 무한 루프에 빠질 가능성이 있으므로 방문 여부를 체크해야 합니다.
• 재귀 호출을 사용하여 구현할때는 스택 오버플로우에 주의해야 합니다.

시간복잡도

DFS의 시간복잡도는 O(V + E)입니다. V는 정점의 수, E는 간선의 수를 나타냅니다.

코드

• 재귀적 구현

  function dfs(graph, start, visited = new Set()) {
    visited.add(start);
  
    // 현재 노드에서 가능한 모든 이웃 노드에 대해 재귀적으로 탐색
    for (const neighbor of graph[start]) {
      if (!visited.has(neighbor)) {
        dfs(graph, neighbor, visited);
      }
    }
  
    // 방문된 노드들을 반환
    return visited;
  }
  
  const graph = {
    A: ["B", "C"],
    B: ["A", "D"],
    C: ["A", "E"],
    D: ["B"],
    E: ["C"],
  };
  
  const start = "A";
  
  // dfs 함수의 리턴값을 받아서 출력
  const visited = dfs(graph, start);
  console.log(Array.from(visited));

• 루프를 사용하여 구현

  function dfs(graph, start) {
    const stack = [start];
    const visited = new Set();
  
    while (stack.length > 0) {
      const vertex = stack.pop();
      if (!visited.has(vertex)) {
        visited.add(vertex);
        for (const neighbor of graph[vertex]) {
          if (!visited.has(neighbor)) {
            stack.push(neighbor);
          }
        }
      }
    }
    return visited;
  }
  
  const graph = {
    A: ["B", "C"],
    B: ["A", "D"],
    C: ["A", "G", "H", "I"],
    D: ["B", "E", "F"],
    E: ["D"],
    F: ["D"],
    G: ["C"],
    H: ["C"],
    I: ["C", "J"],
    J: ["I"],
  };
  //       A
  //     /   \
  //    B     C
  //   /     /|\
  //   D    G H I
  //  / \       /
  // E   F     J
  
  const start = "A";
  const result = dfs(graph, start);
  console.log(result);
  // { 'A', 'C', 'I', 'J', 'H', 'G', 'B', 'D', 'F', 'E' }

  아래의 코드는 위 코드와 방문 순서가 다르지만 dfs 알고리즘의 결과값으로는 유효한 dfs 로직이다.

  function dfs2(graph, start) {
    const stack = [start];
    const visited = new Set();
    visited.add(start);
  
    while (stack.length > 0) {
      const vertex = stack.pop();
      for (const neighbor of graph[vertex]) {
        if (!visited.has(neighbor)) {
          stack.push(neighbor);
          visited.add(neighbor);
        }
      }
    }
  
    return visited;
  }
  
  result = dfs2(graph, start);
  console.log(result);
  // { 'A', 'B', 'C', 'G', 'H', 'I', 'J', 'D', 'E', 'F' }

  bfs 코드와 비교해보면 .pop()만 다르다.

  DFS (Depth-First Search) 알고리즘의 핵심은 시작 노드로부터 시작하여 아직 방문하지 않은 인접 노드를 깊이 우선으로 탐색하는 것입니다. DFS 알고리즘의 정확한 방문 순서는 구현 방식에 따라 다르고, 특히 주어진 그래프의 인접 노드가 어떤 순서로 저장되어 있느냐에 따라 달라질 수 있습니다.

  Set(10) { 'A', 'C', 'I', 'J', 'H', 'G', 'B', 'D', 'F', 'E' } 또는

  Set(10) { 'A', 'B', 'C', 'G', 'H', 'I', 'J', 'D', 'E', 'F' } 모두

  DFS의 결과로 가능합니다. 특히 각 노드의 이웃 노드를 순회하는 순서에 따라 방문 순서가 달라질 수 있습니다.

  따라서, 어떤 결과가 옳다고 할 수 없으며, DFS 알고리즘의 구현 방식에 따라 다르다는 것을 이해하는 것이 중요합니다. 그래프의 모든 노드를 방문하는 것이 목표라면, 두 가지 방식 모두 그 목표를 성공적으로 달성했다고 볼 수 있습니다.

  특정한 방문 순서를 필요로 하는 문제에서는 알고리즘을 조절하여 원하는 결과를 얻을 수 있어야 합니다. 이는 DFS 뿐만 아니라 BFS 등 다른 그래프 탐색 알고리즘에서도 동일하게 적용되는 원칙입니다.