Backtracking

개념

백트래킹은(퇴각검색) 알고리즘 디자인 패러다임의 한 종류로, 모든 가능한 해결책을 생성하고 검증함으로써 문제를 해결하는 방법입니다.

고려할 수 있는 모든 경우의 수 (후보군)를 상태공간트리(State Space Tree)를 통해 표현하고 깊이 우선 탐색을 사용하며 재귀를 통해 모든 가능한 분기를 탐색합니다.

해결책이 아닌 것이 확실할 때 (즉, 조건에 맞지 않을 때), 알고리즘은 즉시 이전 상태로 "백트랙"(다시는 이 후보군을 체크하지 않을 것을 표기)하고, 바로 다른 후보군으로 넘어가며, 결국 최적의 해를 찾는 방법입니다.

해당 루트가 조건에 맞는지를 검사하는 기법을 Promising이라 합니다.

조건에 맞지 않으면 포기하고 다른 루트로 바로 돌아서서, 탐색의 시간을 절약하는 기법을 Pruning (가지치기)이라고 합니다.

즉, 백트래킹은 1) 트리 구조를 기반으로 2) DFS 깊이 탐색을 진행하면서 각 루트에 대해 3) 조건에 부합하는지 체크(Promising), 만약 해당 트리에서 조건에 맞지않는 노드는 더 이상 DFS로 깊이 탐색을 진행하지 않고 4) 가지를 쳐버리고 (Pruning) 해를 찾을때까지 반복됩니다.

장점

1. 모든 가능한 해결책을 찾을 수 있습니다. 따라서, 이론적으로 문제에 대한 최적의 해결책을 찾는 것이 가능합니다.
2. 메모리 사용량이 낮습니다. 이는 해결책을 생성하고 검증하는 것이 메모리에 순차적으로 이루어지기 때문입니다.

단점

1. 시간 복잡도가 매우 높을 수 있습니다. 이는 모든 가능한 분기를 탐색해야 하기 때문입니다.
2. 문제가 너무 커지거나, 문제의 해결책이 많은 경우에는 사용하기 어려울 수 있습니다.

사용에 적합한 상황

백트래킹은 주로 결정 문제(예: 미로 찾기, n-퀸 문제, 스도쿠, 그래프 색칠하기 등)에서 사용되며, 이들 문제는 모든 가능한 해결책을 생성하고 검증하는 것이 요구됩니다.

사용에 부적합한 상황

시간 복잡도가 매우 높을 수 있으므로, 매우 큰 입력 데이터를 다루는 문제나 계산 복잡성이 높은 문제에서는 다른 접근 방식을 고려해야 할 수 있습니다.

주의사항

백트래킹은 종종 재귀 함수를 사용하여 구현되므로, 스택 오버플로우를 조심해야 합니다. 또한, 특정 문제에 대한 모든 가능한 해결책을 찾을 수 있다는 점에서 백트래킹이 유용하지만, 그만큼 비용이 많이 들 수 있으므로 효율성을 항상 고려해야 합니다.

시간복잡도

백트래킹의 시간 복잡도는 문제와 해결책의 수에 따라 다르지만, 일반적으로 최악의 경우 시간 복잡도는 O(n!)입니다.

시간 복잡도에 따라서, 가장 효율적인 알고리즘부터 나열하면 다음과 같습니다:

1. O(n log n)
2. O(n^2)
3. O(n!)

O(n log n)은 퀵소트, 병합소트, 힙소트와 같은 정렬 알고리즘에서 자주 보이는 시간 복잡도입니다. 이들은 일반적으로 대용량 데이터를 처리할 때 효율적입니다.

O(n^2)는 버블 정렬, 삽입 정렬, 선택 정렬 등 기본 정렬 알고리즘에서 자주 나타나는 시간 복잡도입니다. 이들은 작은 데이터 세트에 대해서는 잘 작동하지만, 데이터의 크기가 커질수록 효율성이 떨어집니다.

O(n!)은 일부 브루트 포스(brute-force) 알고리즘 또는 여행 경로 문제(Traveling Salesman Problem)의 해를 찾는 등의 문제에서 나타날 수 있습니다. 이러한 알고리즘은 입력 크기가 증가함에 따라 매우 빠르게 비효율적이 됩니다.

백트래킹 알고리즘을 사용하는 문제들

n-퀸 문제

n-퀸 문제는 대표적인 백트래킹 문제로 n x n 체스판에 n개의 퀸을 서로 공격하지 못하게 배치하는 모든 경우를 찾는 백트래킹 알고리즘입니다.

퀸은 다음과 같이 이동할 수 있으므로, 배치된 퀸 간에 공격할 수 없는 위치로 배치해야 함

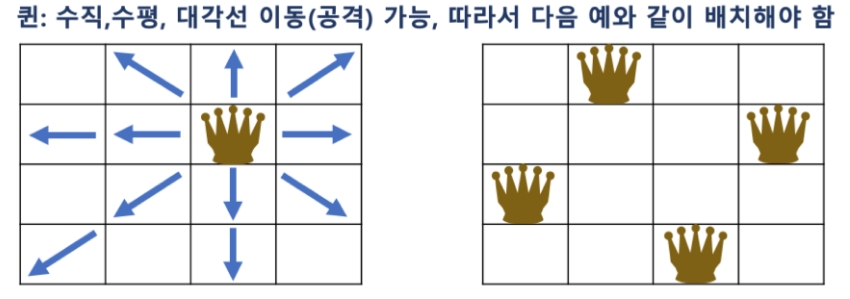
Pruning (가지치기) for N Queen 문제

• 한 행에는 하나의 퀸 밖에 위치할 수 없음 (퀸은 수평 이동이 가능하므로)
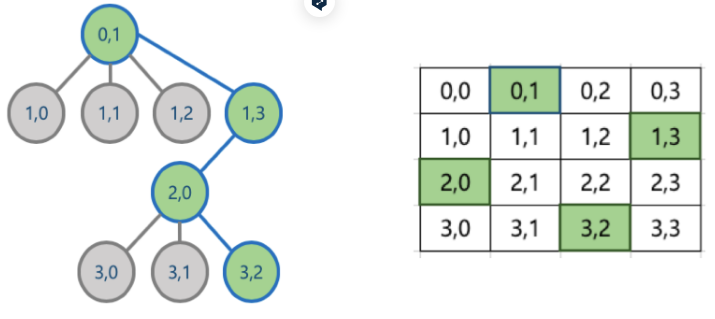
• 맨 위에 있는 행부터 퀸을 배치하고, 다음 행에 해당 퀸이 이동할 수 없는 위치를 찾아 퀸을 배치
• 만약 앞선 행에 배치한 퀸으로 인해, 다음 행에 해당 퀸들이 이동할 수 없는 위치가 없을 경우에는, 더 이상 퀸을 배치하지 않고, 이전 행의 퀸의 배치를 바꿈
  • 즉, 맨 위의 행부터 전체 행까지 퀸의 배치가 가능한 경우의 수를 상태 공간 트리 형태로 만든 후, 각 경우를 맨 위의 행부터 DFS 방식으로 접근, 해당 경우가 진행이 어려울 경우, 더 이상 진행하지 않고, 다른 경우를 체크하는 방식

Promising for N Queen 문제

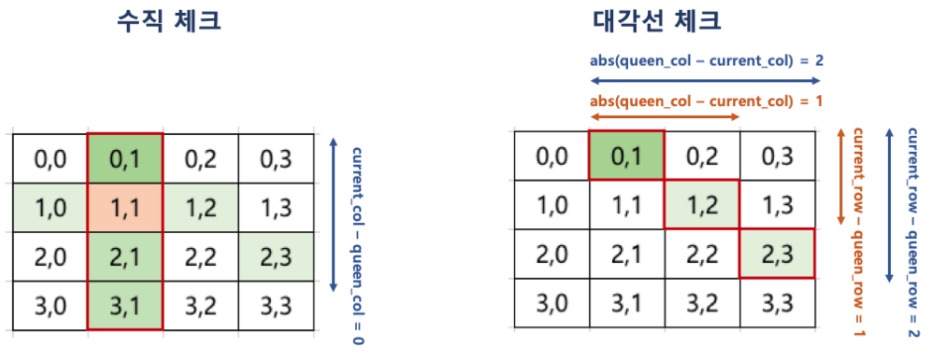
• 해당 루트가 조건에 맞는지를 검사하는 기법을 활용하여,
• 현재까지 앞선 행에서 배치한 퀸이 이동할 수 없는 위치가 있는지를 다음과 같은 조건으로 확인
  • 한 행에 어차피 하나의 퀸만 배치 가능하므로 수평 체크는 별도로 필요하지 않음
• Python

  def is_available(candidate, current_col):
      current_row = len(candidate)
      for queen_row in range(current_row):    
          if candidate[queen_row] == current_col or abs(candidate[queen_row] - current_col) == current_row - queen_row:
              return False
      return True
  
  def DFS(N, current_row, current_candidate, final_result):
      if current_row == N:
          final_result.append(current_candidate[:])
          return
      
      for candidate_col in range(N):
          if is_available(current_candidate, candidate_col):
              current_candidate.append(candidate_col)
              DFS(N, current_row + 1, current_candidate, final_result)
              current_candidate.pop()
  
  def solve_n_queens(N):
      final_result = []
      DFS(N, 0, [], final_result)
      return final_result
  
  solve_n_queens(4)
  // [[1, 3, 0, 2], [2, 0, 3, 1]]

• JS

  // 이 함수는 새로운 퀸을 추가하는 것이 안전한지 확인합니다.
  function isAvailable(candidate, targetCol) {
    // 배치된 퀸의 개수로 현재의 행을 알 수 있음
    const currentRow = candidate.length;
  
    // queenPlacedRow는 이미 퀸이 배치된 행들입니다.
    for (let queenPlacedRow = 0; queenPlacedRow < currentRow; queenPlacedRow++) {
      if (
        // 만약 새 퀸이 배치될 열에 이미 퀸이 있거나 즉, 수직이거나
        candidate[queenPlacedRow] === targetCol ||
        // 대각선 위치에 퀸이 있으면 이 위치에는 퀸을 배치할 수 없습니다.
        // 이미 퀸이 배치된 열 - 검사 대상 열 === 현재 행 - 이미 퀸이 배치된 행
        /**
         * 어떤 퀸이 (4,4)에 있다고 합시다.
         * 이 퀸은 대각선 상으로 이동하며 (3,3), (2,2), (1,1) 또는 (5,5), (6,6), (7,7) 등의 위치로 이동할 수 있습니다.
         * 각 위치에 대해 행과 열의 차이를 계산해 보면, 모두 동일함을 알 수 있습니다. 즉, 행과 열의 차이가 동일한 위치는 대각선 상에 위치한다는 것을 의미합니다.
         * 따라서, Math.abs(candidate[queenPlacedRow] - targetCol)는 이미 배치된 퀸의 위치와 새로운 퀸의 위치의 열 차이를 계산하고,
         * currentRow - queenPlacedRow는 행 차이를 계산합니다.
         * 두 차이가 같으면, 두 퀸은 대각선 상에 있다는 것을 의미합니다.
         * 따라서, 이 코드는 새로운 퀸이 대각선 상에 있는지를 체크하는 로직이 됩니다.
         */
        Math.abs(candidate[queenPlacedRow] - targetCol) ===
          currentRow - queenPlacedRow
        // quuenPlacedRow + candidate[quuenPlacedRow] === currentRow + targetCol
      ) {
        return false;
      }
    }
  
    // 위의 경우가 아니면, 퀸을 배치할 수 있습니다.
    return true;
  }
  
  // 이 함수는 깊이 우선 탐색을 사용하여 N-Queens 문제의 모든 해결책을 찾습니다.
  function dfs(boardSize, currentRow, currentCandidate, finalResult) {
    // 모든 행에 퀸이 배치되면, 이 배치를 결과에 추가합니다.
    if (currentRow === boardSize) {
      finalResult.push(currentCandidate.slice());
      return;
    }
  
    // 각 열에 대해 퀸을 배치하려고 시도합니다.
    for (let targetCol = 0; targetCol < boardSize; targetCol++) {
      // 만약 이 열에 퀸을 안전하게 배치할 수 있다면,
      if (isAvailable(currentCandidate, targetCol)) {
        // 퀸을 이 열에 배치합니다.
        currentCandidate.push(targetCol);
  
        // 다음 행으로 이동합니다.
        dfs(boardSize, currentRow + 1, currentCandidate, finalResult);
  
        // 퀸을 이 열에서 제거하여 다른 열에 배치할 수 있게 합니다.
        /**
         * candidate.pop();의 역할은 두 가지 상황에서 중요합니다:
         * 만약 유효한 targetCol이 발견되지 않으면, 즉 isAvailable()이 실패하면, 그 시점의 candidate 배열은 해결책이 될 수 없습니다. 
         * 따라서 candidate.pop();는 현재 행의 퀸 위치를 제거하고 이전 행(또는 스택의 이전 레벨)으로 돌아가 다른 가능한 위치를 탐색하게 됩니다. 이것이 백트래킹의 본질입니다.
         * 만약 isAvailable()이 성공하고 currentRow가 boardSize에 도달하여 모든 퀸이 성공적으로 배치된다면, candidate는 잠재적인 해결책이 됩니다. 그러나 이는 특정 해결책일 뿐, 다른 가능한 해결책이 있을 수 있으므로, 이 시점에서 candidate.pop();를 사용하여 마지막 행의 퀸 위치를 제거하고 이전 행으로 돌아가 다른 가능한 위치를 탐색합니다. 이렇게 해서 모든 가능한 해결책을 찾을 수 있습니다.
         */
        currentCandidate.pop();
      }
    }
  }
  
  // 이 함수는 N-Queens 문제의 모든 해결책을 찾습니다.
  function solveNQueens(boardSize) {
    // finalResult는 모든 가능한 퀸의 배치를 저장합니다.
    const finalResult = [];
  
    // dfs 함수를 호출하여 첫 번째 행에서 시작합니다.
    dfs(boardSize, 0, [], finalResult);
  
    // 모든 해결책을 반환합니다.
    return finalResult;
  }
  
  // 4-Queens 문제의 해결책을 찾습니다.
  console.log(solveNQueens(4));
  // Expected output: [[1, 3, 0, 2], [2, 0, 3, 1]]

  이 코드는 4x4 체스판에 4개의 퀸을 서로 공격하지 못하게 배치하는 방법을 찾습니다. 해결책이 없다면 "Solution does not exist"를 출력합니다.

미로 찾기

미로에서 출발점에서 도착점까지의 경로를 찾는 백트래킹 알고리즘입니다. 미로는 2차원 배열로 표현되며, 1은 벽을, 0은 경로를 나타냅니다.

function solveMaze(maze, x, y, solution) {
    const n = maze.length;
    if(x === n - 1 && y === n - 1 && maze[x][y] === 1) {
        solution[x][y] = 1;
        return true;
    }
    if(isSafe(maze, x, y, n)) {
        solution[x][y] = 1;
        if (solveMaze(maze, x + 1, y, solution)) {
            return true;
        }
        if (solveMaze(maze, x, y + 1, solution)) {
            return true;
        }
        solution[x][y] = 0;
        return false;
    }
    return false;
}

function isSafe(maze, x, y, n) {
    return (x >= 0 && y >= 0 && x < n && y < n && maze[x][y] === 1);
}

let maze = [
    [1, 0, 0, 0],
    [1, 1, 0, 1],
    [0, 1, 0, 0],
    [1, 1, 1, 1]
];
let solution = new Array(maze.length).fill(0).map(() => new Array(maze.length).fill(0));

if (solveMaze(maze, 0, 0, solution)) {
    console.log(solution);
} else {
    console.log("No solution found");
}

이 코드는 (0, 0)에서 시작하여 (n-1, n-1)로 가는 경로를 찾습니다. 만약 경로가 없다면 "No solution found"를 출력합니다.

스도쿠

9x9 스도쿠 퍼즐을 해결하는 백트래킹 알고리즘입니다.

function solveSudoku(grid, row, col, n) {
    if (row === n - 1 && col === n) {
        return true;
    }
    if (col === n) {
        row++;
        col = 0;
    }
    if (grid[row][col] > 0) {
        return solveSudoku(grid, row, col + 1, n);
    }
    for (let num = 1; num <= n; num++) {
        if (isSafe(grid, row, col, num, n)) {
            grid[row][col] = num;
            if (solveSudoku(grid, row, col + 1, n)) {
                return true;
            }
        }
        grid[row][col] = 0;
    }
    return false;
}

function isSafe(grid, row, col, num, n) {
    for (let x = 0; x <= 8; x++) {
        if (grid[row][x] === num) {
            return false;
        }
    }
    for (let x = 0; x <= 8; x++) {
        if (grid[x][col] === num) {
            return false;
        }
    }
    let startRow = row - row % 3, startCol = col - col % 3;
    for (let i = 0; i < 3; i++) {
        for (let j = 0; j < 3; j++) {
            if (grid[i + startRow][j + startCol] === num) {
                return false;
            }
        }
    }
    return true;
}
let grid = [
    [3, 0, 6, 5, 0, 8, 4, 0, 0],
    [5, 2, 0, 0, 0, 0, 0, 0, 0],
    [0, 8, 7, 0, 0, 0, 0, 3, 1],
    [0, 0, 3, 0, 1, 0, 0, 8, 0],
    [9, 0, 0, 8, 6, 3, 0, 0, 5],
    [0, 5, 0, 0, 9, 0, 6, 0, 0],
    [1, 3, 0, 0, 0, 0, 2, 5, 0],
    [0, 0, 0, 0, 0, 0, 0, 7, 4],
    [0, 0, 5, 2, 0, 6, 3, 0, 0]
];

if (solveSudoku(grid, 0, 0, 9)) {
    console.log(grid);
} else {
    console.log("No solution found");
}

그래프 색칠하기

주어진 그래프에 m개의 색을 사용하여 인접한 두 노드가 같은 색상을 가지지 않도록 색칠하는 방법을 찾는 백트래킹 알고리즘입니다.

function graphColoring(graph, color, pos, m) {
    const n = graph.length;
    if (pos === n) {
        return true;
    }
    for (let c = 1; c <= m; c++) {
        if (isSafe(graph, color, pos, c)) {
            color[pos] = c;
            if (graphColoring(graph, color, pos + 1, m)) {
                return true;
            }
            color[pos] = 0;
        }
    }
    return false;
}

function isSafe(graph, color, pos, c) {
    for (let i = 0; i < graph.length; i++) {
        if (graph[pos][i] && c === color[i]) {
            return false;
        }
    }
    return true;
}

let graph = [
    [0, 1, 1, 1],
    [1, 0, 1, 0],
    [1, 1, 0, 1],
    [1, 0, 1, 0]
];
let color = new Array(graph.length).fill(0);

if (!graphColoring(graph, color, 0, 3)) {
    console.log("Solution does not exist");
} else {
    console.log(color);
}

이 코드는 주어진 그래프를 3가지 색으로 색칠하는 방법을 찾습니다. 해결책이 없다면 "Solution does not exist"를 출력합니다.

부분집합 구하기

function getSubsets(inputSet, tempList = [], start = 0) {
  // start는 현재까지 고려된 배열 요소 이후의 인덱스를 나타냅니다.
  let list = [[...tempList]];
  for (let i = start; i < inputSet.length; i++) {
    // 배열 inputSet의 i 번째 요소를 tempList에 추가합니다. 이는 새로운 부분집합을 만드는 단계입니다.
    tempList.push(inputSet[i]);
    // 재귀 호출을 통해 현재까지 생성된 부분집합에 inputSet의 나머지 요소를 추가하여 새로운 부분집합들을 생성합니다.
    let result = getSubsets(inputSet, tempList, i + 1);
    // 재귀 호출이 끝나면 tempList의 마지막 요소를 제거합니다. 이렇게 하면 tempList는 다음 반복에서 이전 상태로 돌아갑니다.
    tempList.pop();
    // 재귀 호출로 생성된 새로운 부분집합들을 list에 추가합니다.
    list = list.concat(result);
  }
  return list;
}

console.log(getSubsets([1, 2, 3]));

/*
[
  [],       [ 1 ],
  [ 1, 2 ], [ 1, 2, 3 ],
  [ 1, 3 ], [ 2 ],
  [ 2, 3 ], [ 3 ]
]
*/

이 코드는 주어진 숫자 배열에 대한 모든 부분집합을 생성하는 백트래킹 알고리즘을 구현한 것입니다.

[1, 2, 3]의 부분집합을 구하는 경우로 시뮬레이션 해보면 다음과 같습니다:

1. 최초에 getSubsets([1, 2, 3])를 호출합니다. 이 때 tempList는 빈 배열이고, start는 0입니다.
2. 빈 배열이 부분집합이므로 이를 list에 추가합니다. (list = [[]])
3. 반복문을 통해 inputSet의 각 요소(1, 2, 3)에 대해 재귀 호출을 진행합니다.
   • tempList에 1을 추가하고, getSubsets([1, 2, 3], [1], 1)를 호출합니다.
     • 이 호출에서 1이 포함된 부분집합들 ([1], [1, 2], [1, 3], [1, 2, 3])을 list에 추가합니다.
   • tempList에서 1을 제거하고, tempList에 2를 추가한 후 getSubsets([1, 2, 3], [2], 2)를 호출합니다.
     • 이 호출에서 2만 포함된 부분집합들 ([2], [2, 3])을 list에 추가합니다.
   • tempList에서 2를 제거하고, tempList에 3을 추가한 후 getSubsets([1, 2, 3], [3], 3)를 호출합니다.
     • 이 호출에서 3만 포함된 부분집합 ([3])을 list에 추가합니다.
4. 모든 부분집합이 추가된 list를 반환합니다. 따라서 결과는 [[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3]]가 됩니다.

백트래킹 알고리즘을 최적화하는 일반적인 방법은 재귀 호출을 최소화하고, 불필요한 계산을 줄이는 것입니다. 그러나 이는 대부분 문제의 경우에 따라 다르며, 특정 문제에 대한 지식이 필요합니다.

위 모든 코드들은 백트래킹 알고리즘을 사용합니다. 백트래킹 알고리즘의 특징과 사용된 코드들의 공통점을 몇 가지 나열해보면 다음과 같습니다:

1. 탐색의 순서: 문제의 해결을 위해 가능한 모든 해를 탐색하는데, 이때 깊이 우선 탐색(DFS, Depth-First Search) 방식을 사용합니다. 예를 들어, 미로 찾기에서는 현재 위치에서 가능한 방향을 하나씩 시도해보고, 그 결과를 기반으로 다시 가능한 방향을 탐색하는 과정을 반복합니다.
2. 가지치기(Pruning): 백트래킹 알고리즘의 핵심 요소 중 하나는 가지치기입니다. 탐색 과정에서 이미 알고 있는 정보를 바탕으로 해결책이 될 수 없는 경로는 미리 배제함으로써 불필요한 탐색을 줄입니다. 이를 통해 알고리즘의 효율성을 높입니다.
3. 상태 공간의 복원: 백트래킹 알고리즘은 이전 상태로 돌아갈 수 있어야 합니다. 그래서 코드에서는 재귀 호출을 통해 현재 상태를 저장하고 복원하는 과정을 반복하게 됩니다. 만약 특정 경로가 해결책으로 이어지지 않는다면, 이전 상태로 돌아가 다른 경로를 탐색합니다.
4. 해결 가능성 검사: 각 단계에서 해결책으로 이어질 가능성이 있는지를 확인하는 isSafe() 함수가 사용됩니다. 이 함수는 문제에 따라 다르게 정의되며, 미로 찾기에서는 벽이나 미로의 범위를 벗어나지 않는지, n-퀸 문제에서는 퀸이 서로 공격할 수 없는지, 스도쿠에서는 같은 숫자가 행, 열, 그리고 같은 3x3 박스에 없는지, 그래프 색칠에서는 인접한 노드에 같은 색이 없는지를 확인합니다.