개념
프림 알고리즘은 크루스칼 알고리즘과 함께 그래프에서 최소 신장 트리를 찾는 알고리즘 중 하나입니다. 시작점을 선택하고, 선택된 정점들과 인접한 간선들 중에서 가장 작은 가중치를 가진 간선과 연결된 정점을 트리에 추가하는 방식으로 작동합니다.
크루스칼 알고리즘과의 비교
- 둘다, 탐욕 알고리즘을 기초로 합니다.
- Kruskal's algorithm은 가장 가중치가 작은 간선부터 선택하면서 MST를 구합니다.
- Prim's algorithm은 특정 정점에서 시작, 해당 정점에 연결된 가장 가중치가 작은 간선을 선택, 간선으로 연결된 정점들에 연결된 간선 중에서 가장 가중치가 작은 간선을 택하는 방식으로 MST를 구함
로직 프로세스
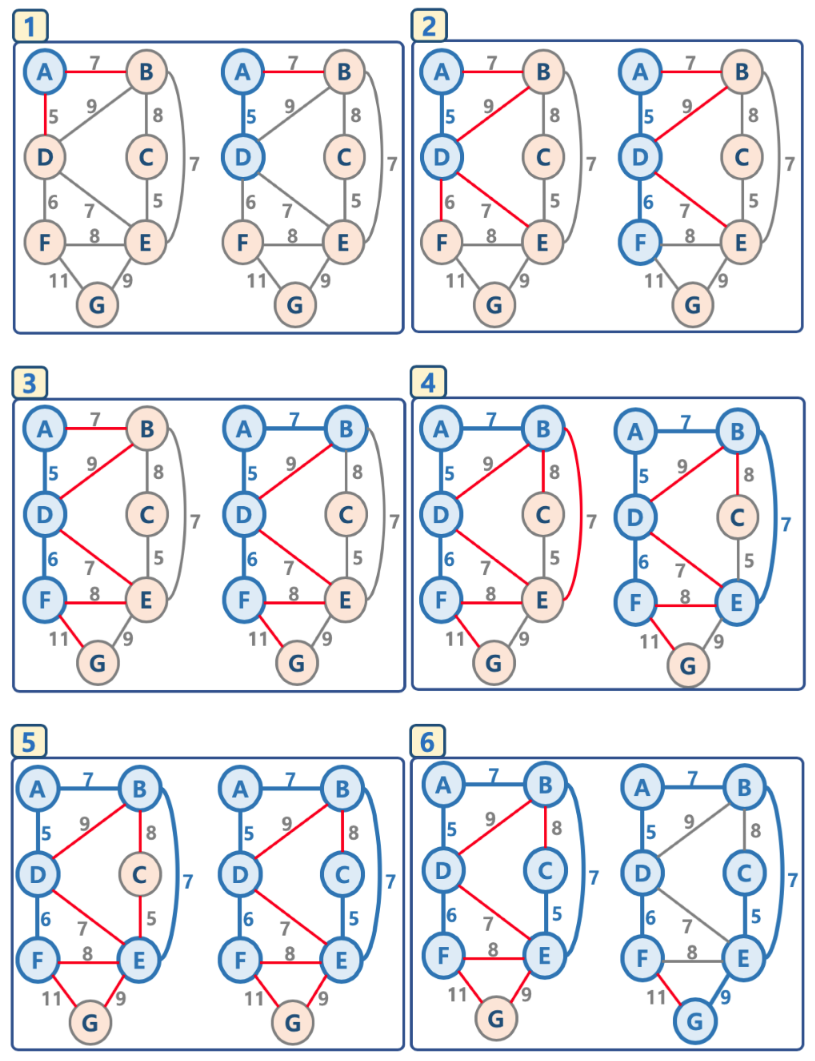
- 시작 노드를 선택하고, 연결된 노드 집합에 추가합니다.
- 연결된 노드 집합에서 연결 가능한 간선 중 가장 가중치가 작은 간선을 찾습니다.
- 해당 간선으로 연결된 노드가
- 연결된 노드 집합에 이미 들어 있다면 스킵합니다.(cycle 방지)
- 연결된 노드 집합에 들어 있지 않으면 해당 간선을 선택하고 해당 간선 정보를 '최소 신장 트리'에 삽입, 노드는 연결된 노드 집합에 추가합니다.
- 추출한 간선은 간선 리스트에서 제거
- 모든 노드가 연결된 노드 집합에 포함될 때(간선 리스트에 더 이상의 간선이 없을 때)까지 2-4단계를 반복합니다.
장점
프림 알고리즘이 크루스칼 알고리즘에 비해 가지는 장점 중 하나는 간선의 수가 많은 그래프에서 더 효율적으로 작동한다는 것입니다. 크루스칼 알고리즘은 모든 간선을 검사해야 하므로 간선의 수가 많을수록 시간 복잡도가 높아집니다. 반면에, 프림 알고리즘은 이미 방문한 정점과 연결된 간선만을 고려하므로, 간선의 수가 많아도 정점의 수에 더 비례한 시간 복잡도를 갖습니다. 따라서, 간선의 수가 많지만 각 정점의 차수(해당 정점과 연결된 간선의 수)가 상대적으로 작은 그래프에서는 프림 알고리즘이 더 효율적입니다. 그러나 정점의 수에 비해 간선의 수가 상대적으로 적은 그래프에서는 크루스칼 알고리즘이 더 효율적일 수 있습니다.
단점
반면에, 프림 알고리즘은 시작 노드에서부터 가까운 노드들부터 MST를 생성하기 때문에, 전체적인 MST의 가중치를 최소화하는 데 있어서 항상 최적의 결과를 보장하지는 않습니다.
사용에 적합한 상황
간선의 수가 많은 밀집 그래프(dense graph)에서 프림 알고리즘이 크루스칼 알고리즘보다 더 효율적으로 작동합니다.
사용에 부적합한 상황
간선의 수가 적은 희소 그래프(sparse graph)에서는 크루스칼 알고리즘이 더 효율적일 수 있습니다.
주의사항
프림 알고리즘을 적용할 때는 그래프가 연결 그래프인지 확인해야 합니다. 그렇지 않으면 알고리즘이 제대로 작동하지 않을 수 있습니다.
시간복잡도
프림 알고리즘의 시간 복잡도는 O(E log V)입니다. 여기서 E는 간선의 수, V는 정점의 수입니다.
- 최초 key 생성 시간 복잡도: 𝑂(𝑉)
- while 구문과 keys.popitem() 의 시간 복잡도는 𝑂(𝑉𝑙𝑜𝑔𝑉)
- while 구문은 V(노드 갯수) 번 실행됨
- heap 에서 최소 key 값을 가지는 노드 정보 추출 시(pop)의 시간 복잡도: 𝑂(𝑙𝑜𝑔𝑉)
- for 구문의 총 시간 복잡도는 𝑂(𝐸𝑙𝑜𝑔𝑉)
- for 구문은 while 구문 반복시에 결과적으로 총 최대 간선의 수 E만큼 실행 가능 𝑂(𝐸)
- for 구문 안에서 key값 변경시마다 heap 구조를 변경해야 하며, heap 에는 최대 V 개의 정보가 있으므로 𝑂(𝑙𝑜𝑔𝑉)
일반적인 heap 자료 구조 자체에는 본래 heap 내부의 데이터 우선순위 변경시, 최소 우선순위 데이터를 루트노드로 만들어주는 로직은 없음. 이를 decrease key 로직이라고 부름, 해당 로직은 heapdict 라이브러리를 활용해서 간단히 적용가능
- 따라서 총 시간 복잡도는 𝑂(𝑉+𝑉𝑙𝑜𝑔𝑉+𝐸𝑙𝑜𝑔𝑉)이며,
- O(V)는 전체 시간 복잡도에 큰 영향을 미치지 않으므로 삭제,
- E > V 이므로 (최대 V^2 = E 가 될 수 있음), 𝑂((𝑉+𝐸)𝑙𝑜𝑔𝑉)는 간단하게 𝑂(𝐸𝑙𝑜𝑔𝑉)로 나타낼 수 있음
코드
JS
function prim(graph) {
const nodes = graph.vertices;
const edges = graph.edges;
const mst = [];
const visited = new Set();
const edgeQueue = new PriorityQueue(); // 우선순위 큐를 이용
let current = nodes[0]; // 첫 노드를 선택
visited.add(current);
while (visited.size !== nodes.length) {
for (let edge of edges) {
// 방문하지 않은 노드 중 가장 작은 가중치의 간선을 찾음
if (edge.src === current && !visited.has(edge.dest)) {
edgeQueue.enqueue(edge, edge.weight);
}
}
let nextEdge = edgeQueue.dequeue(); // 가장 작은 가중치의 간선을 선택
while (nextEdge && visited.has(nextEdge.dest)) { // 이미 방문한 노드라면 스킵
nextEdge = edgeQueue.dequeue();
}
if (!nextEdge) {
// 모든 노드를 방문했다면 종료
break;
}
mst.push(nextEdge);
visited.add(nextEdge.dest);
current = nextEdge.dest;
}
return mst;
}
우선순위 큐를 사용한 개선된 프림 알고리즘 코드
기존 프림 알고리즘과 개선된 프림 알고리즘의 가장 큰 차이는
기존 프림 알고리즘은 간선을 기준으로 우선순위 큐를 사용하고
개선된 프림 알고리즘은 노드를 기준으로 우선순위 큐를 사용한다.
보통 노드의 수가 간선의 수 보다 적다. 간선의 수는 노드의 제곱이다.
따라서 노드를 기준으로 우선순위큐를 사용하면 시간 복잡도가 개선될 수 있다.
기존 프림: ElogE
개선된 프림: ElogV
class PriorityQueue {
constructor() {
this.heap = [null];
}
getParentIndex(i) {
return Math.floor(i / 2);
}
getLeftChildIndex(i) {
const index = i * 2;
return index < this.heap.length ? index : null;
}
getRightChildIndex(i) {
const index = i * 2 + 1;
return index < this.heap.length ? index : null;
}
swap(i1, i2) {
[this.heap[i1], this.heap[i2]] = [this.heap[i2], this.heap[i1]];
}
push(node) {
this.heap.push(node);
this.bubbleUp();
}
bubbleUp() {
let currentIndex = this.heap.length - 1;
let parentIndex = this.getParentIndex(currentIndex);
while (
currentIndex > 1 &&
this.heap[currentIndex][1] < this.heap[parentIndex][1]
) {
this.swap(currentIndex, parentIndex);
currentIndex = parentIndex;
parentIndex = this.getParentIndex(currentIndex);
}
}
pop() {
const smallest = this.heap[1];
const endNode = this.heap.pop();
if (this.heap.length > 1) {
this.heap[1] = endNode;
this.bubbleDown();
}
return smallest;
}
bubbleDown() {
let currentIndex = 1;
let leftChildIndex = this.getLeftChildIndex(currentIndex);
let rightChildIndex = this.getRightChildIndex(currentIndex);
while (this.heap[leftChildIndex] || this.heap[rightChildIndex]) {
let smallestIndex = rightChildIndex;
if (
!smallestIndex ||
(this.heap[leftChildIndex] &&
this.heap[rightChildIndex] &&
this.heap[leftChildIndex][1] < this.heap[rightChildIndex][1])
) {
smallestIndex = leftChildIndex;
}
if (this.heap[currentIndex][1] > this.heap[smallestIndex][1]) {
this.swap(currentIndex, smallestIndex);
currentIndex = smallestIndex;
leftChildIndex = this.getLeftChildIndex(currentIndex);
rightChildIndex = this.getRightChildIndex(currentIndex);
} else {
break;
}
}
}
isEmpty() {
return this.heap.length === 1;
}
}
function primMST(graph, start) {
// 리턴값
let mst = [],
totalWeight = 0;
// 우선순위 큐
let pq = new PriorityQueue();
pq.push([start, 0]);
// 초기화 필요 변수
let visited = {},
parent = {},
minEdgeWeight = {};
// 초기화
for (let node of Object.keys(graph)) {
minEdgeWeight[node] = Infinity; // 1. 모든 노드의 최소 가중치를 무한대로,
parent[node] = null; // 2. 부모 노드를 null로,
visited[node] = false; // 3. 방문 여부를 false로 설정합니다.
}
minEdgeWeight[start] = 0; // 'start' 노드의 최소 가중치를 0으로 설정합니다.
// 개선할 수 있는 부분
// let visitedCount = 0;
// let totalNodes = Object.keys(graph).length;
// while (!pq.isEmpty() && visitedCount < totalNodes) {
// 우선 순위 큐가 빌 때까지 반복합니다.
while (!pq.isEmpty()) {
let [currentNode, currentWeight] = pq.pop(); // 우선 순위 큐에서 가장 작은 노드를 꺼냅니다.
if (visited[currentNode]) continue; // 현재 노드가 이미 방문되었다면 컨티뉴..
visited[currentNode] = true; // 방문 표시를 합니다.
// visitedCount++; // 개선할 수 있는 부분: 방문한 노드의 수를 증가시킵니다.
// 부모 노드가 null이 아니라면 최소 신장 트리에 추가하고 총 가중치를 더합니다.
// 프림(Prim)의 알고리즘에서는 시작 노드의 부모를 null로 설정하고, 나머지 노드들의 부모를 찾아나가면서 트리를 구성합니다.
// 이렇게 하면, 시작 노드는 제외하고 나머지 노드들만이 정확히 한 번씩 최소 신장 트리에 추가되며, 이를 통해 올바른 최소 신장 트리를 구성할 수 있습니다.
if (parent[currentNode] !== null) {
mst.push([parent[currentNode], currentNode, currentWeight]);
totalWeight += currentWeight;
}
// 현재 노드와 연결된 모든 노드를 확인합니다.
for (let [adjacent, weight] of Object.entries(graph[currentNode])) {
// 연결된 노드가 아직 방문되지 않았고, 연결된 노드의 가중치가 현재 최소 가중치보다 작다면,
// 아직 MST에 추가되지 않은 노드를 향하는 간선 중에서 가장 가중치가 작은 간선을 찾음
if (!visited[adjacent] && weight < minEdgeWeight[adjacent]) {
parent[adjacent] = currentNode; // 부모 노드를 현재 노드로 설정하고,
minEdgeWeight[adjacent] = weight; // 최소 가중치를 업데이트하고,
pq.push([adjacent, minEdgeWeight[adjacent]]); //연결된 노드를 우선 순위 큐에 추가합니다.
}
}
}
// 반복문이 종료되면, 최소 신장 트리와 그의 총 가중치를 반환합니다.
return { mst, totalWeight };
}
// const graph = {
// A: { B: 7, D: 5 },
// B: { A: 7, D: 8, E: 7, C: 8 },
// C: { B: 8, E: 5 },
// D: { A: 5, B: 8, E: 7, F: 6 },
// E: { B: 7, D: 7, C: 5, F: 8, G: 9 },
// F: { D: 6, E: 8, G: 11 },
// G: { E: 9, F: 11 },
// };
const graph = {
A: { B: 3, C: 1, D: 5 },
B: { A: 3, C: 6, E: 9, F: 5 },
C: { A: 1, B: 6, D: 2, F: 4 },
D: { A: 5, C: 2, F: 6, G: 3 },
E: { B: 9, F: 3 },
F: { B: 5, C: 4, D: 6, E: 3, G: 7, H: 5 },
G: { D: 3, F: 7, H: 9 },
H: { F: 5, G: 9 },
};
let { mst, totalWeight } = primMST(graph, "A");
console.log("MST:", mst);
console.log("Total Weight:", totalWeight);이 코드에서 개선할 부분이 있다면 모든 노드가 다 방문되었더라도 큐에 노드가 남아있으면 의미없는 루프가 발생한다. 방문한 노드의 수가 전체 노드의 수와 같다면 종료시키는 로직이 들어가면 의미없는 루프를 줄일 수 있을것같다.
Python
myedges = [
(7, 'A', 'B'), (5, 'A', 'D'),
(8, 'B', 'C'), (9, 'B', 'D'), (7, 'B', 'E'),
(5, 'C', 'E'),
(7, 'D', 'E'), (6, 'D', 'F'),
(8, 'E', 'F'), (9, 'E', 'G'),
(11, 'F', 'G')
]
from collections import defaultdict
from heapq import *
def prim(start_node, edges):
mst = list()
adjacent_edges = defaultdict(list)
for weight, n1, n2 in edges:
adjacent_edges[n1].append((weight, n1, n2))
adjacent_edges[n2].append((weight, n2, n1))
connected_nodes = set(start_node)
candidate_edge_list = adjacent_edges[start_node]
heapify(candidate_edge_list)
while candidate_edge_list:
weight, n1, n2 = heappop(candidate_edge_list)
if n2 not in connected_nodes:
connected_nodes.add(n2)
mst.append((weight, n1, n2))
for edge in adjacent_edges[n2]:
if edge[2] not in connected_nodes:
heappush(candidate_edge_list, edge)
return mst
prim ('A', myedges)
```
개선된 프림 알고리즘
```python
from heapdict import heapdict
def prim(graph, start):
mst, keys, pi, total_weight = list(), heapdict(), dict(), 0
for node in graph.keys():
keys[node] = float('inf')
pi[node] = None
keys[start], pi[start] = 0, start
while keys:
current_node, current_key = keys.popitem()
mst.append([pi[current_node], current_node, current_key])
total_weight += current_key
for adjacent, weight in mygraph[current_node].items():
if adjacent in keys and weight < keys[adjacent]:
keys[adjacent] = weight
pi[adjacent] = current_node
return mst, total_weight
mygraph = {
'A': {'B': 7, 'D': 5},
'B': {'A': 7, 'D': 9, 'C': 8, 'E': 7},
'C': {'B': 8, 'E': 5},
'D': {'A': 5, 'B': 9, 'E': 7, 'F': 6},
'E': {'B': 7, 'C': 5, 'D': 7, 'F': 8, 'G': 9},
'F': {'D': 6, 'E': 8, 'G': 11},
'G': {'E': 9, 'F': 11}
}
mst, total_weight = prim(mygraph, 'A')
print ('MST:', mst)
print ('Total Weight:', total_weight)