Graph

개념 설명

그래프는 정점(Vertex)과 간선(Edge)으로 이루어진 자료구조로, 각 정점들은 간선으로 연결되어 있는 관계를 나타냅니다.

그래프(Graph)는 데이터 간의 관계를 표현하기 위한 자료구조입니다. 그래프 역시 비선형 구조이며, 트리의 일반적인 개념입니다. 트리도 일종의 그래프 중 하나에 속합니다.

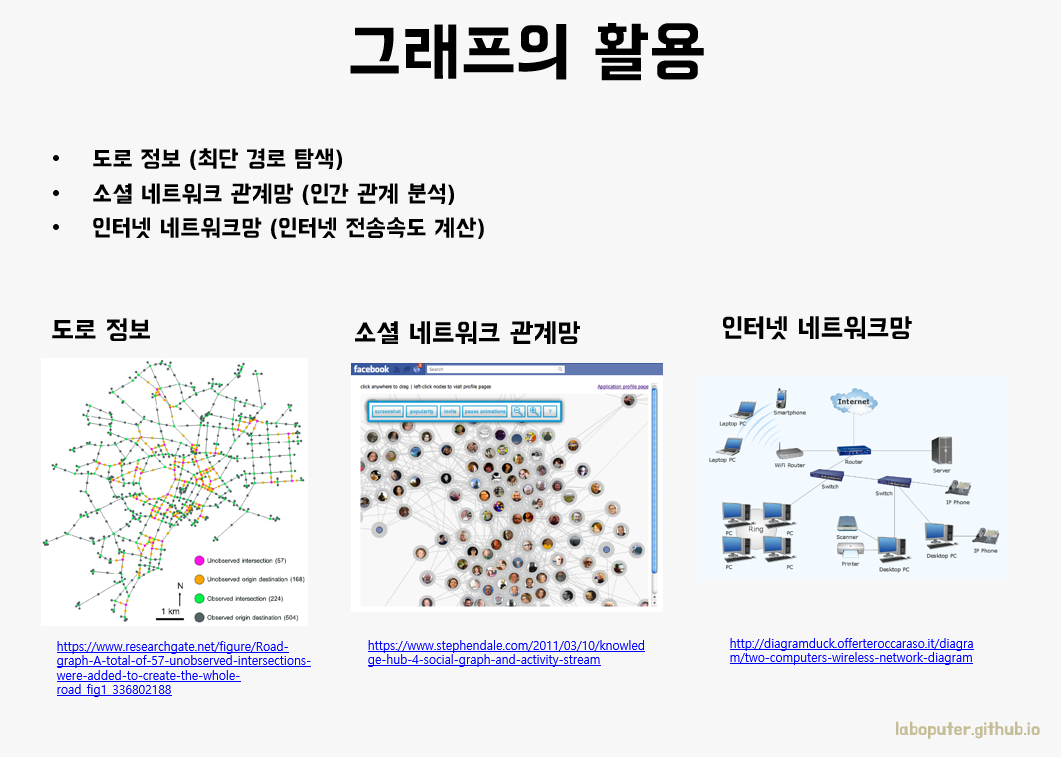
그래프는 현실 세계의 다양한 상호 관계를 모델링하고 표현하는 데 사용됩니다. 그래프는 네트워크, 지도, 소셜 네트워크, 전자 회로 등 다양한 분야에서 활발하게 사용됩니다.

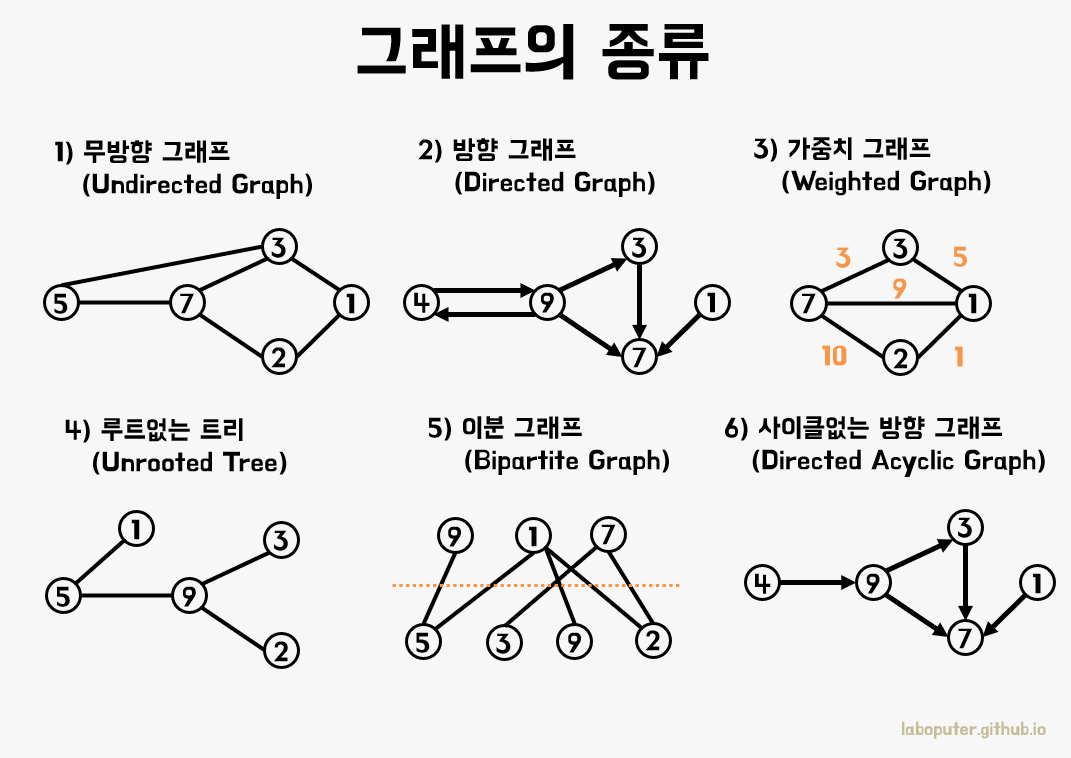
용어 설명

• Vertex (정점): 트리의 노드라 생각하면 됨
• Edge (엣지/링크): (4, 6)과 같은 식으로 표현
• Degree (정점의 차수): 무방향 그래프에서 하나의 정점에 인접한 정점의 수, 그래프 전체의 디그리는 가장 크기가 큰 차수를 의미
• 인접성 표현
  • 노드 4와 6은 인접하다 와 같이 표현 (Adjacent)
  • 엣지를 기준으로 표현할때는 e = (4, 6), 엣지 e는 노드 4 또는 노드 6과 인접하다 (Incident)
• In-Degree (진입 차수): 방향 그래프에서 외부에서 오는 간선의 수
• Out-Degree (진출 차수): 방향 그래프에서 외부로 향하는 간선의 수
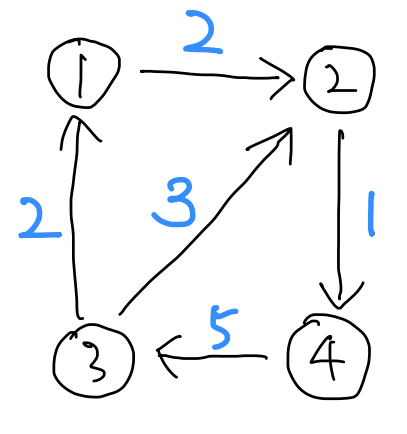
• Path (경로): 두 개 이상의 정점을 지나는 경로, 정점이 중복되면 안됨 1→2→4, 1→3→4, 1→3→5→4
• Path Length (경로 길이): 경로를 구성하기 위해 사용된 간선의 수
• Simple Path (단순 경로): 처음 정점과 끝 정점을 제외하고 중복된 정점이 없는 경로
• Cycle (사이클): 단순 경로의 시작 정점과 종료 정점이 동일한 경우, 1→2→4→3→1
• Sparse 그래프
  • 노드 갯수에 비해서 엣지 갯수가 상대적으로 작은 그래프
• Dense 그래프
  • 노드 갯수에 비해서 엣지 갯수가 상대적으로 많은 그래프

이진 트리와의 비교

	그래프	트리
정의	노드와 노드를 연결하는 간선으로 표현되는 자료구조	그래프의 한 종류로, 방향성이 있는 비순환 그래프
방향성	방향 / 무방향 둘 다 존재	방향 (하위 자식 노드 방향으로)
사이클	순환 / 비순환 둘 다 존재	비순환
루트 노드	존재하지 않음	존재함
부모 / 자식 관계	존재하지 않음	존재함

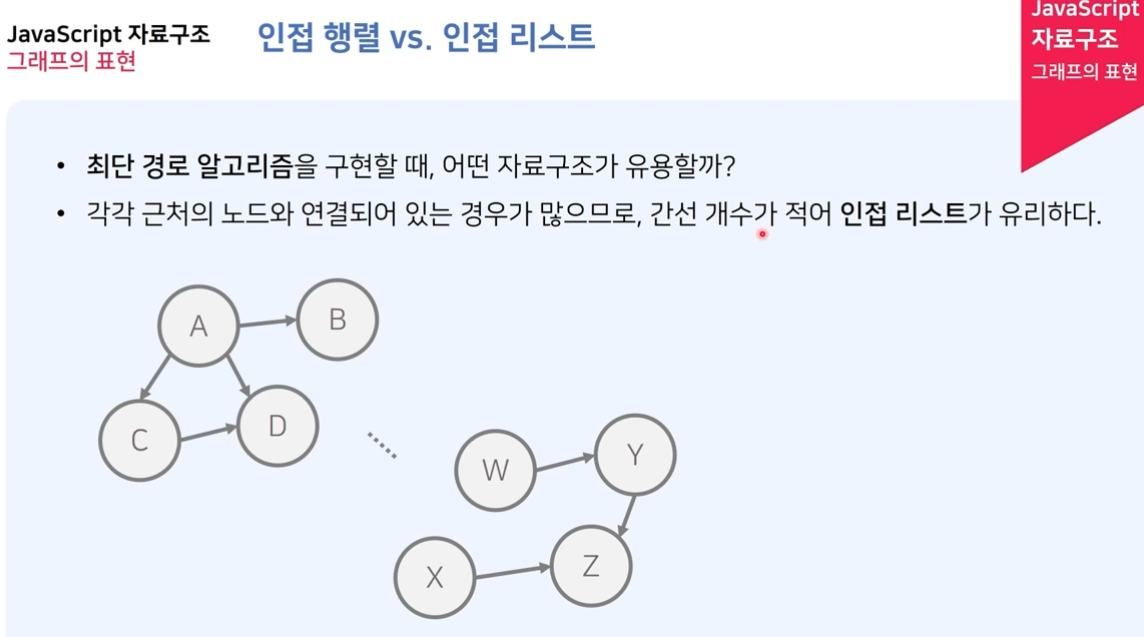
그래프의 인접성을 표현하는 방식 두 가지

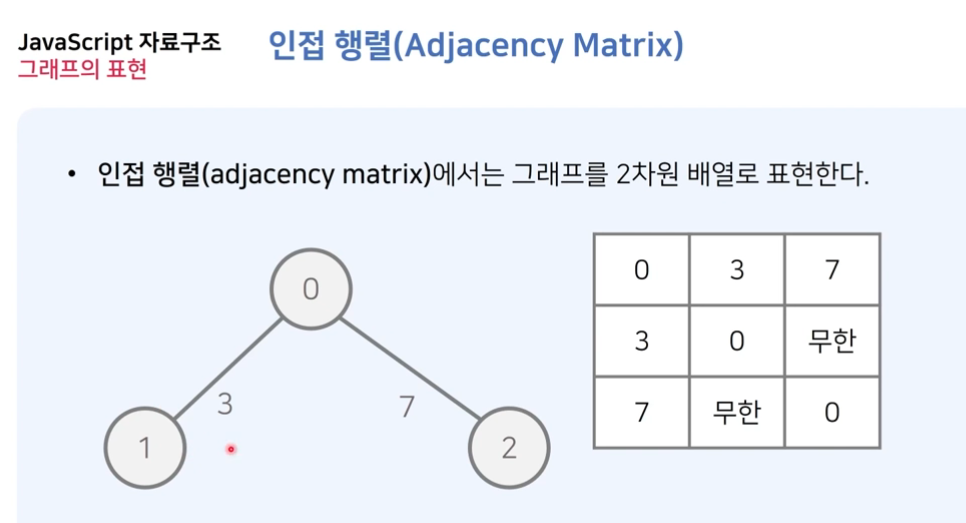
• 1) 인접 행렬 (adjacency matrix)

  

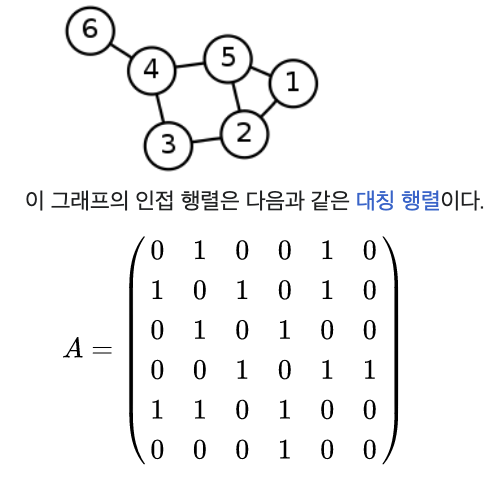
  N by N 행렬로 2차원 배열 또는 테이블로 이해하면된다.

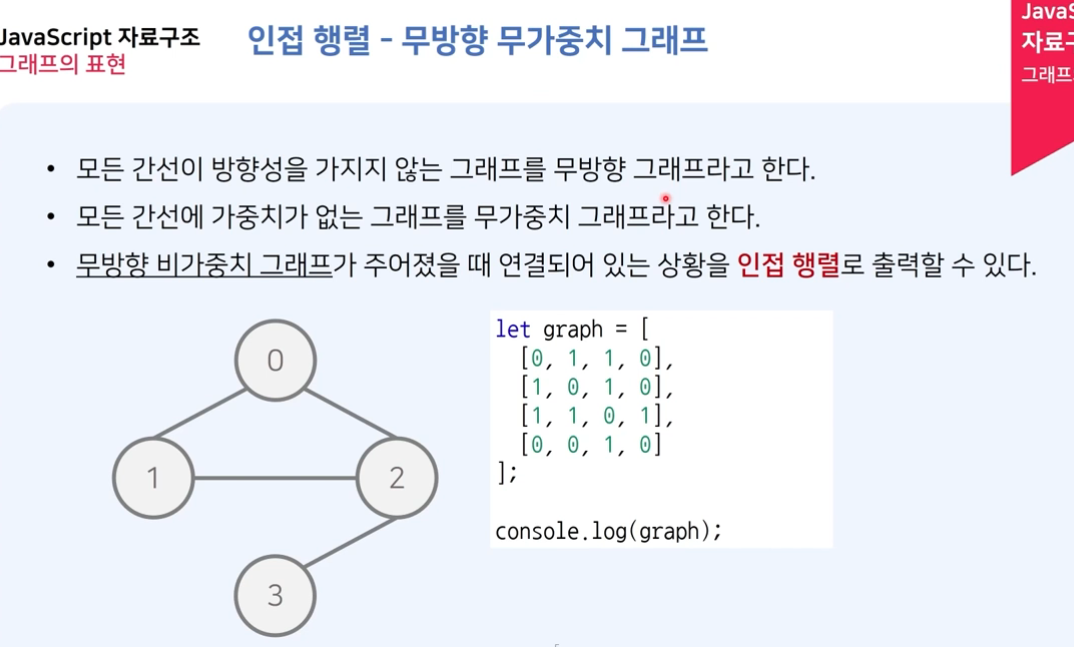
  • 엣지가 존재하면 1, 없으면 0으로 표현한다.
  • 좌측 상단에서 우측 하단으로 대각선을 그어 접으면 대칭이 됨을 볼 수 있다.
  • 자기 자신과의 엣지는 1, 0 둘 중 하나로 일관되게 정의하면 된다. 위 그림에서는 0으로 설정하였다.
  • 단점
    • N^2의 요소를 갖는데 반해 엔트리가 적은 경우 필요없는 공간이 너무 많으므로 메모리가 낭비된다. 예를들어 위 첫 번째 이미지에서 엣지는 7개이고 양 방향이므로 14개이다. 전체 요소수는 6x6=36 이므로 14/36과 같이 22개의 요소가 크게 의미가 없으므로 메모리가 낭비되게된다.
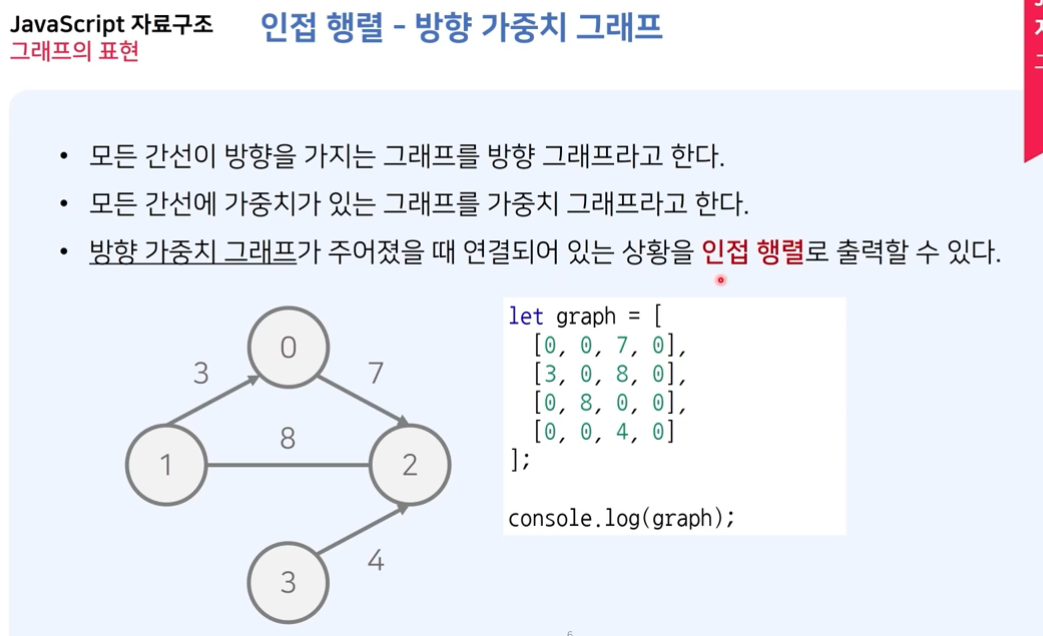
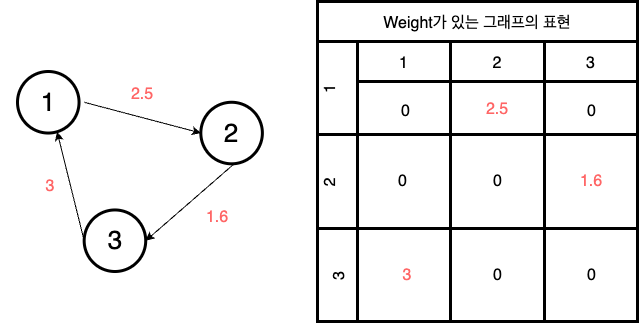
  • Weight가 있는 그래프에서는 아래와 같이 인접행렬 테이블로 표현할 수 있다.

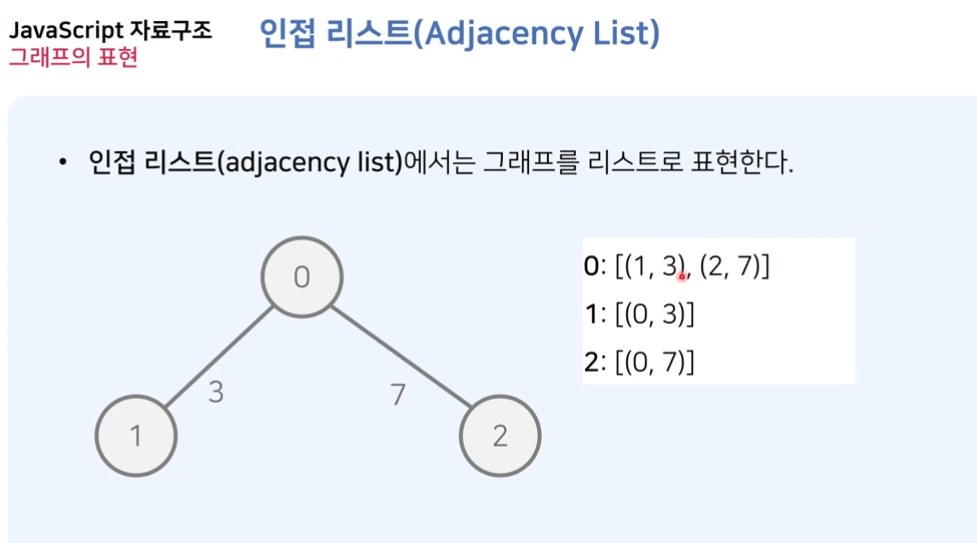
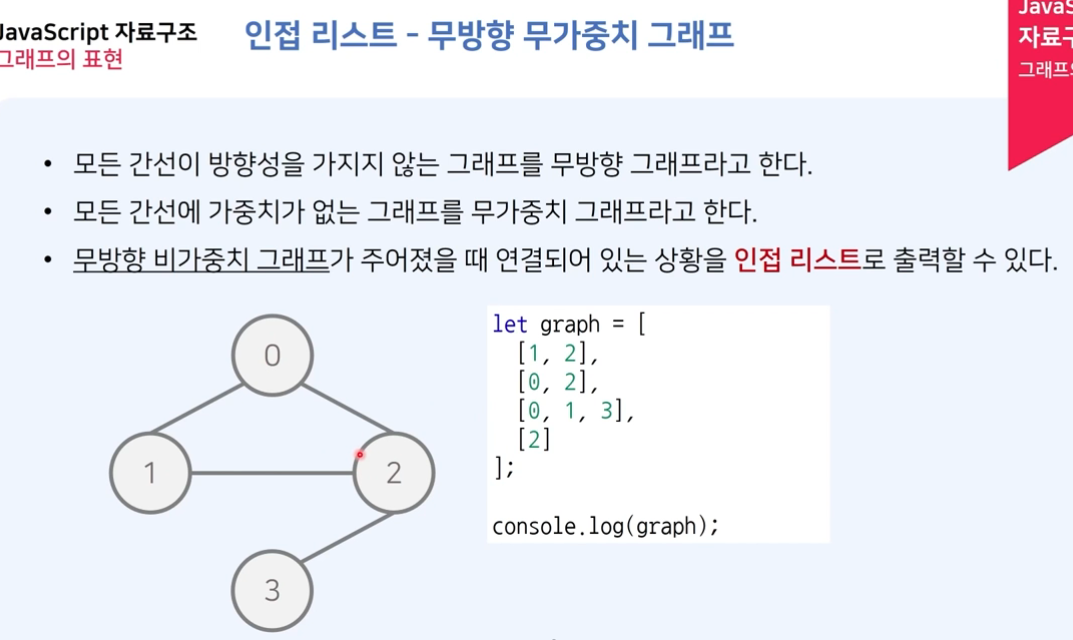
• 2) 인접 리스트 (adjacency list)

  

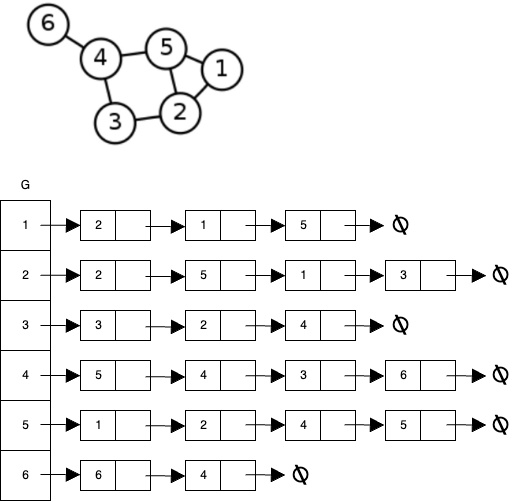
  adjacency list의 list는 링크드 리스트를 의미한다.

  • 그래프 G는 정점을 배열로 표현하고 우측에는 링크드 리스트로 인접한 정점을 연결한다. 이때 인접한 노드의 순서는 관계없다.
  • 위 인접 리스트에서는 자기 자신도 포함한것이다.
  • 인접 정점을 위 그림에서는 한 방향으로 표현하였지만 양방향으로도 표현할 수 있다.

• 인접 행렬 VS 인접 리스트 비교

  
  
  

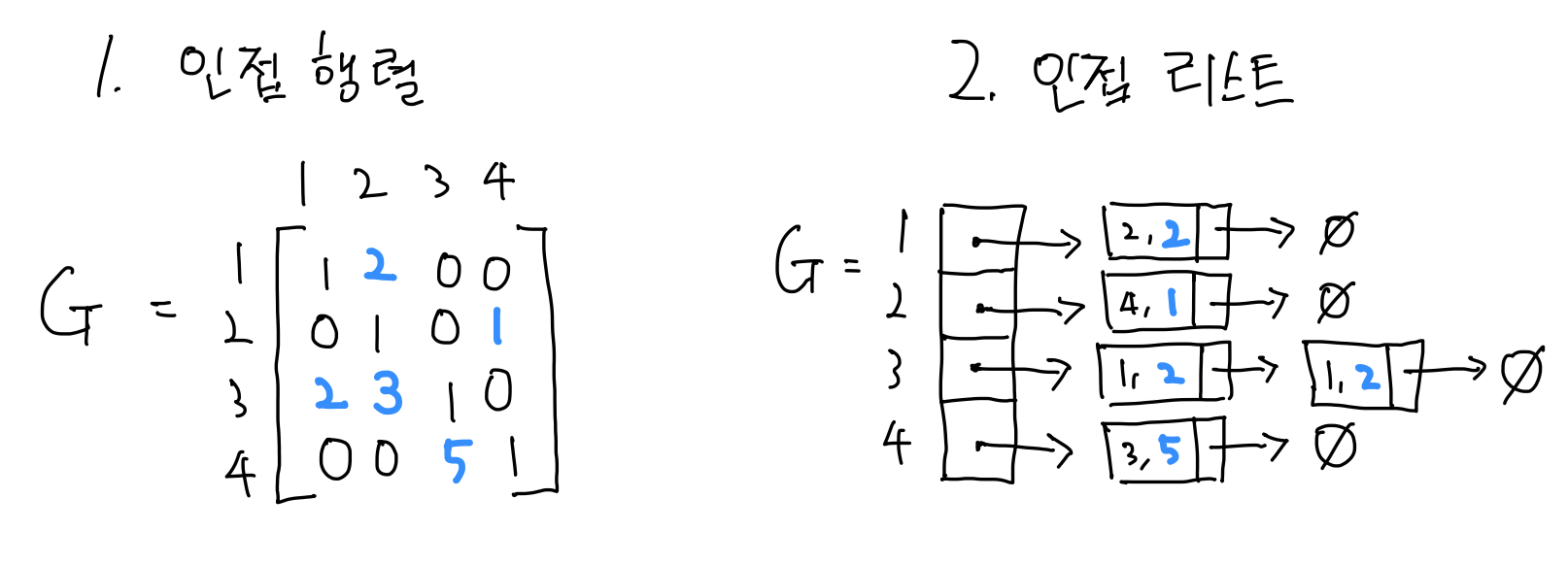
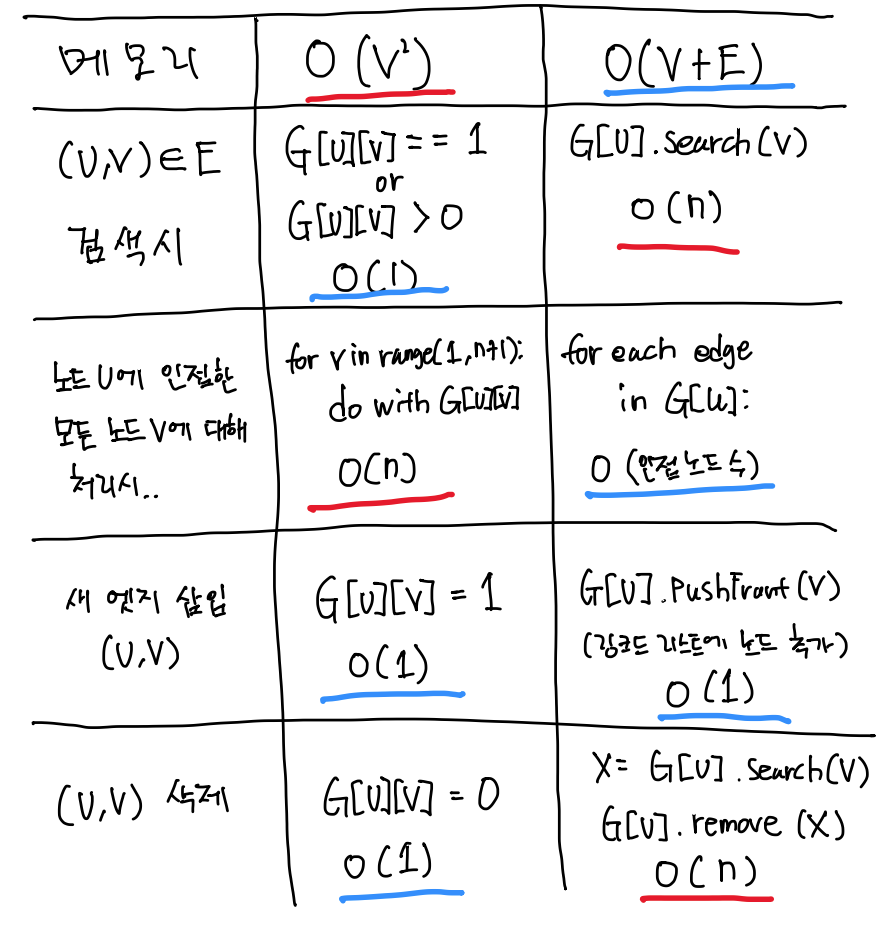
장점

• 다양한 형태의 관계를 표현할 수 있어 실제 문제에 적합한 모델링이 가능합니다.
• 다양한 알고리즘을 활용하여 복잡한 문제를 해결할 수 있습니다.
• 탐색, 경로 찾기, 최단 경로 등 다양한 그래프 알고리즘을 적용할 수 있습니다.

단점

• 그래프 자료구조의 크기가 커질수록 메모리 사용량이 증가할 수 있습니다.
• 일부 그래프 알고리즘은 시간 복잡도가 높아 효율적인 구현이 필요합니다.

사용에 적합한 상황

• 네트워크나 관계를 나타내는 문제에서 사용할 수 있습니다.
• 최단 경로, 탐색, 연결 여부 등을 파악해야 하는 문제에 사용될 수 있습니다.

사용에 부적합한 상황

• 간선의 수가 적은 경우에는 그래프 자료구조보다 다른 자료구조가 더 효율적일 수 있습니다.
• 간선이 방향성이 없고 가중치가 없는 경우에는 배열이나 리스트 등 단순한 자료구조가 더 적합할 수 있습니다.

주의사항

• 그래프에서 사이클이 발생하는지 확인하여 무한 루프를 방지해야 합니다.
• 그래프의 크기와 구조에 따라 알고리즘의 효율성이 달라지므로 문제에 적합한 알고리즘을 선택해야 합니다.
  

시간 복잡도

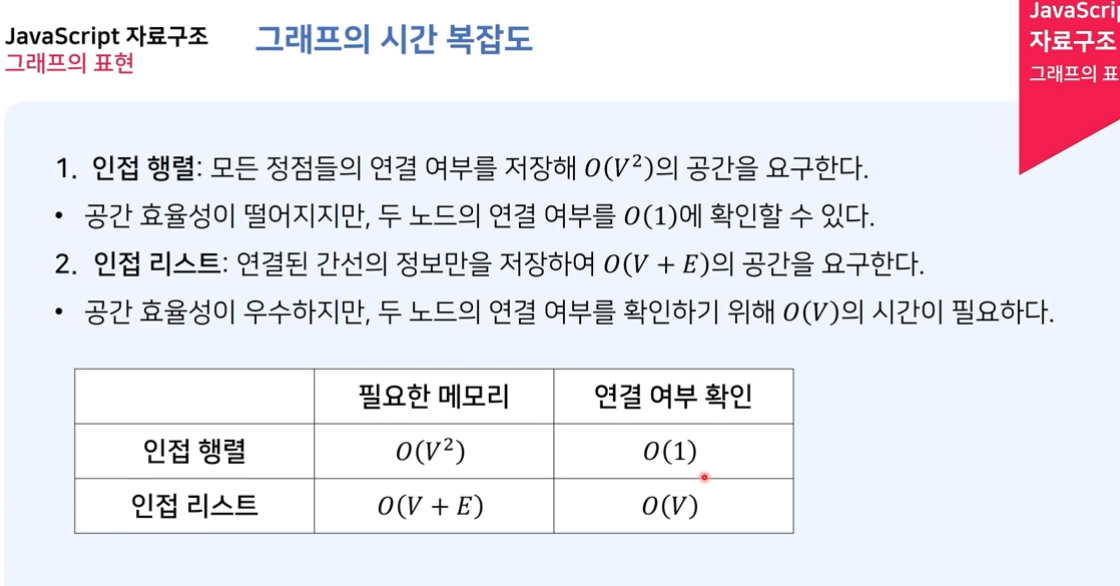
• 그래프의 크기에 따라 다양한 알고리즘의 시간 복잡도가 존재합니다. 대표적으로 깊이 우선 탐색(DFS)과 너비 우선 탐색(BFS)의 시간 복잡도는 O(V + E)입니다. 최단 경로 알고리즘인 다익스트라 알고리즘의 시간 복잡도는 O((V + E) log V)입니다.

코드 구현

그래프는 일반적으로 인접 리스트(Adjacency List)나 인접 행렬(Adjacency Matrix)을 활용하여 표현할 수 있습니다. 자바스크립트에서는 객체를 사용하여 인접 리스트를 구현하는 것이 일반적입니다. 예를 들어, 다음은 무방향 그래프를 인접 리스트로 표현하는 예제

class Graph {
  constructor() {
    this.adjacencyList = new Map();
  }

  addVertex(vertex) {
    this.adjacencyList.set(vertex, []);
  }

  addEdge(vertex1, vertex2) {
    this.adjacencyList.get(vertex1).push(vertex2);
    this.adjacencyList.get(vertex2).push(vertex1);
  }
}

// 그래프 생성
const graph = new Graph();

// 정점 추가
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');

// 간선 추가
graph.addEdge('A', 'B');
graph.addEdge('B', 'C');