힙이란?
힙(Heap)은 특별한 유형의 완전 이진 트리(Complete Binary Tree)입니다.
이진 트리는 각 노드가 최대 두 개의 자식 노드를 가지는 트리이며,
완전 이진 트리는 마지막 레벨을 제외한 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가장 왼쪽부터 채워집니다.
힙은 다음 두 가지 속성을 가지는 완전 이진 트리입니다:
"모든 레벨이 완전히 채워진 트리"라는 표현은 주로 완전 이진 트리(Complete Binary Tree)에 대해 사용되는데, 이는 트리의 모든 레벨이 완전히 채워져 있고, 마지막 레벨이라면 왼쪽부터 순서대로 채워져 있는 특징을 가진 이진 트리를 의미합니다.
완전 이진 트리에서는 각 레벨의 모든 노드가 왼쪽부터 차례대로 채워져 있습니다. 예를 들어, 루트 노드만 있는 트리는 레벨 1에 하나의 노드가 있으므로 완전 이진 트리입니다. 또한 루트 노드 밑에 왼쪽과 오른쪽 자식 노드가 있는 트리는 레벨 2에 두 개의 노드가 있으므로 완전 이진 트리입니다.
1
/ \
2 3
/ \ / \
4 5 6 7하지만 레벨 2에 왼쪽 자식 노드만 있고 오른쪽 자식 노드가 없는 트리는 완전 이진 트리가 아닙니다. 왜냐하면 완전 이진 트리에서는 각 레벨의 모든 노드가 왼쪽부터 차례대로 채워져 있어야 하기 때문입니다.
아래의 트리에서, 두 번째 레벨의 노드 중 오른쪽 노드(2의 오른쪽 자식)가 빠져 있습니다. 이는 완전 이진 트리의 정의에 어긋납니다. 완전 이진 트리에서는 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있어야 하며, 마지막 레벨에서는 왼쪽부터 차례대로 노드가 채워져 있어야 합니다.
1
/ \
2 3
/ / \
4 6 7완전 이진 트리는 힙과 같은 자료구조를 구현하는 데 사용되며, 배열을 이용해 효율적으로 표현할 수 있습니다. 이 때문에 힙과 같은 자료구조에서는 완전 이진 트리를 사용하는 것이 일반적입니다.
- 모든 노드의 값은 자식 노드의 값보다 크거나 같습니다. (이러한 힙을 최대 힙(Max Heap)이라고 합니다)
- 모든 노드의 값은 자식 노드의 값보다 작거나 같습니다. (이러한 힙을 최소 힙(Min Heap)이라고 합니다)
이러한 속성 덕분에 힙은 자료의 저장 및 검색에 있어서 다양한 용도로 활용됩니다.
-
힙 상세 설명
-
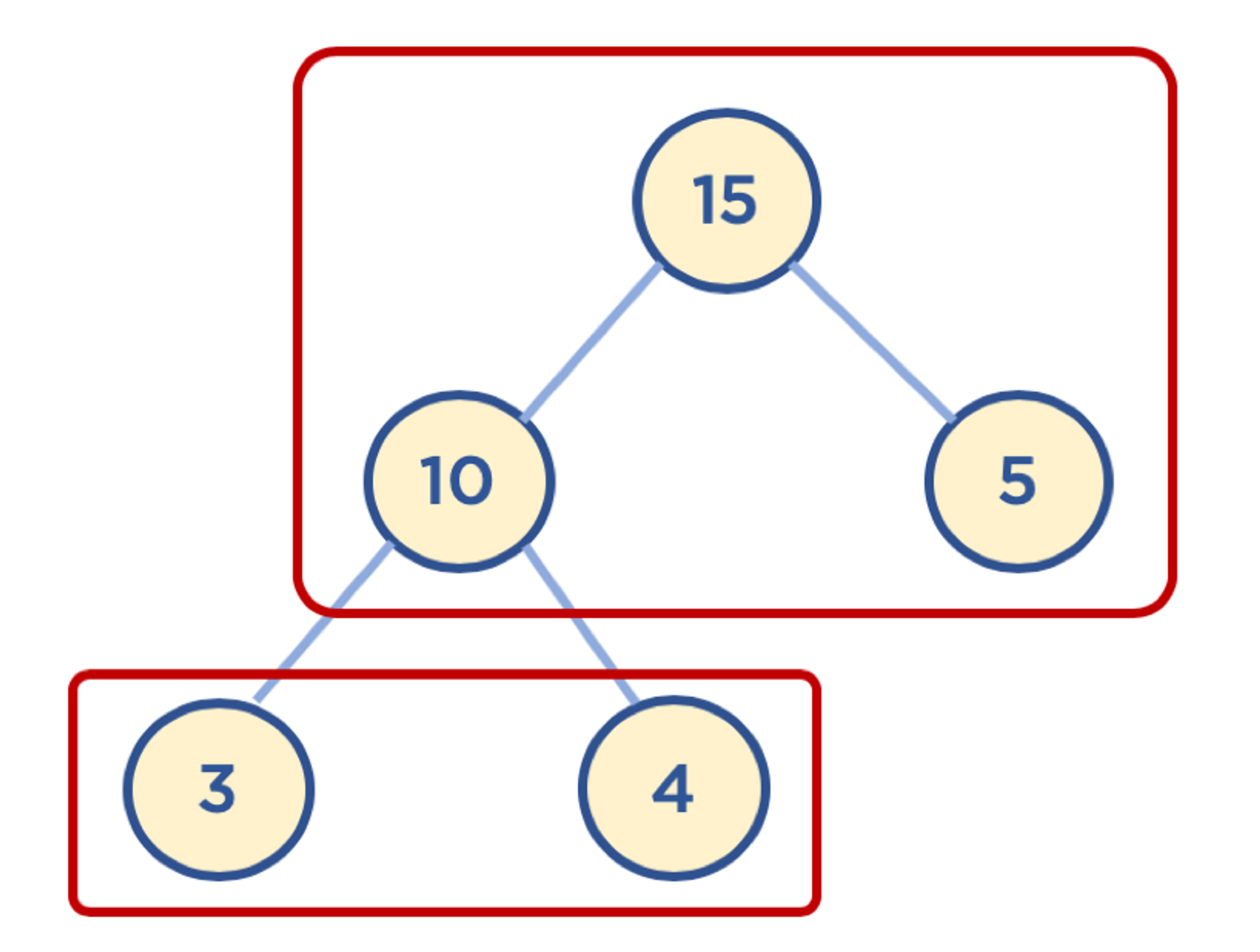
힙: 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)
- 완전 이진 트리: 노드를 삽입할 때 최하단 왼쪽 노드부터 차례대로 삽입하는 트리
-
힙을 사용하는 이유
- 배열에 데이터를 넣고, 최대값과 최소값을 찾으려면 O(n) 이 걸림
- 이에 반해, 힙에 데이터를 넣고, 최대값과 최소값을 찾으면, O(log n)이 걸림
- 우선순위 큐와 같이 최대값 또는 최소값을 빠르게 찾아야 하는 자료구조 및 알고리즘 구현 등에 활용됨힙 (Heap) 구조
- 힙은 최대값을 구하기 위한 구조 (최대 힙, Max Heap) 와, 최소값을 구하기 위한 구조 (최소 힙, Min Heap) 로 분류할 수 있음
- 힙은 다음과 같이 두 가지 조건을 가지고 있는 자료구조임
- 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다
- 최대 힙의 경우 크거나 같다.
- 최소 힙의 경우 작거나 같다.
- 완전 이진 트리 형태를 가짐
- 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다
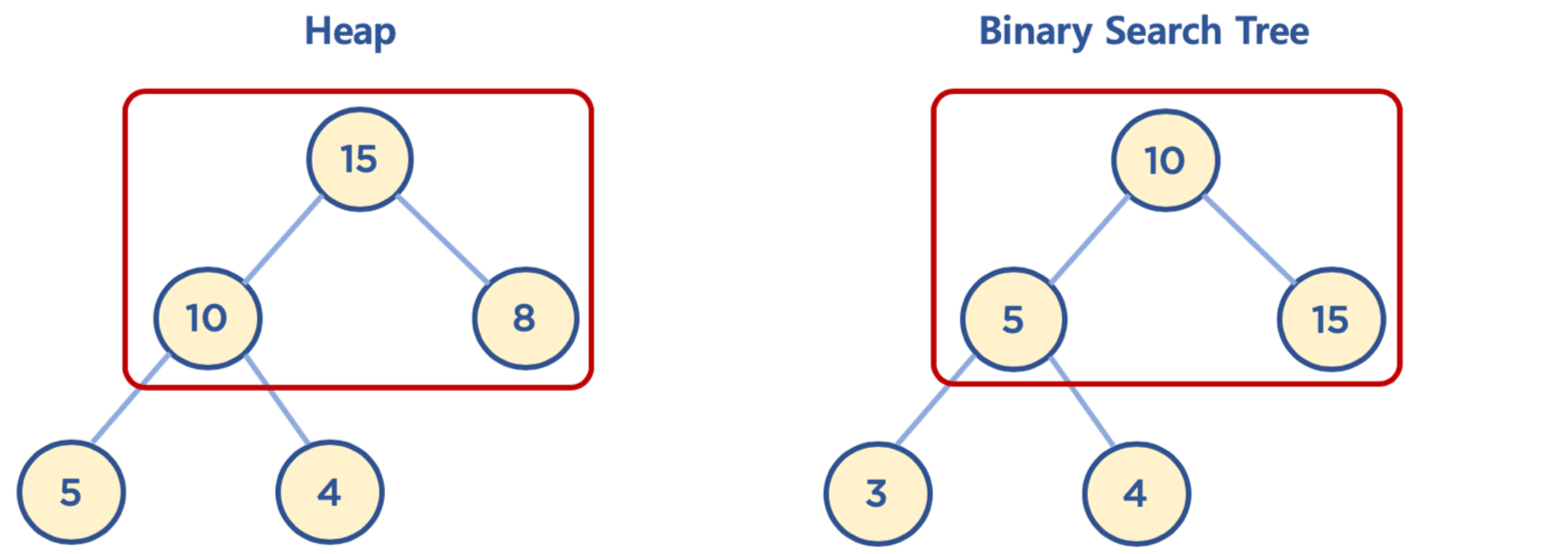
힙과 이진 탐색 트리의 공통점과 차이점
- 공통점: 힙과 이진 탐색 트리는 모두 이진 트리임
- 차이점:
- 힙은 각 노드의 값이 자식 노드보다 크거나 같음(Max Heap의 경우)
- 이진 탐색 트리는 왼쪽 자식 노드의 값이 가장 작고, 그 다음 부모 노드, 그 다음 오른쪽 자식 노드 값이 가장 큼
- 힙은 이진 탐색 트리의 조건인 자식 노드에서 작은 값은 왼쪽, 큰 값은 오른쪽이라는 조건은 없음
- 힙의 왼쪽 및 오른쪽 자식 노드의 값은 오른쪽이 클 수도 있고, 왼쪽이 클 수도 있음
- 이진 탐색 트리는 탐색을 위한 구조라 볼 수 있고
- 힙은 최대/최소값 검색을 위한 구조 중 하나로 이해하면 됨
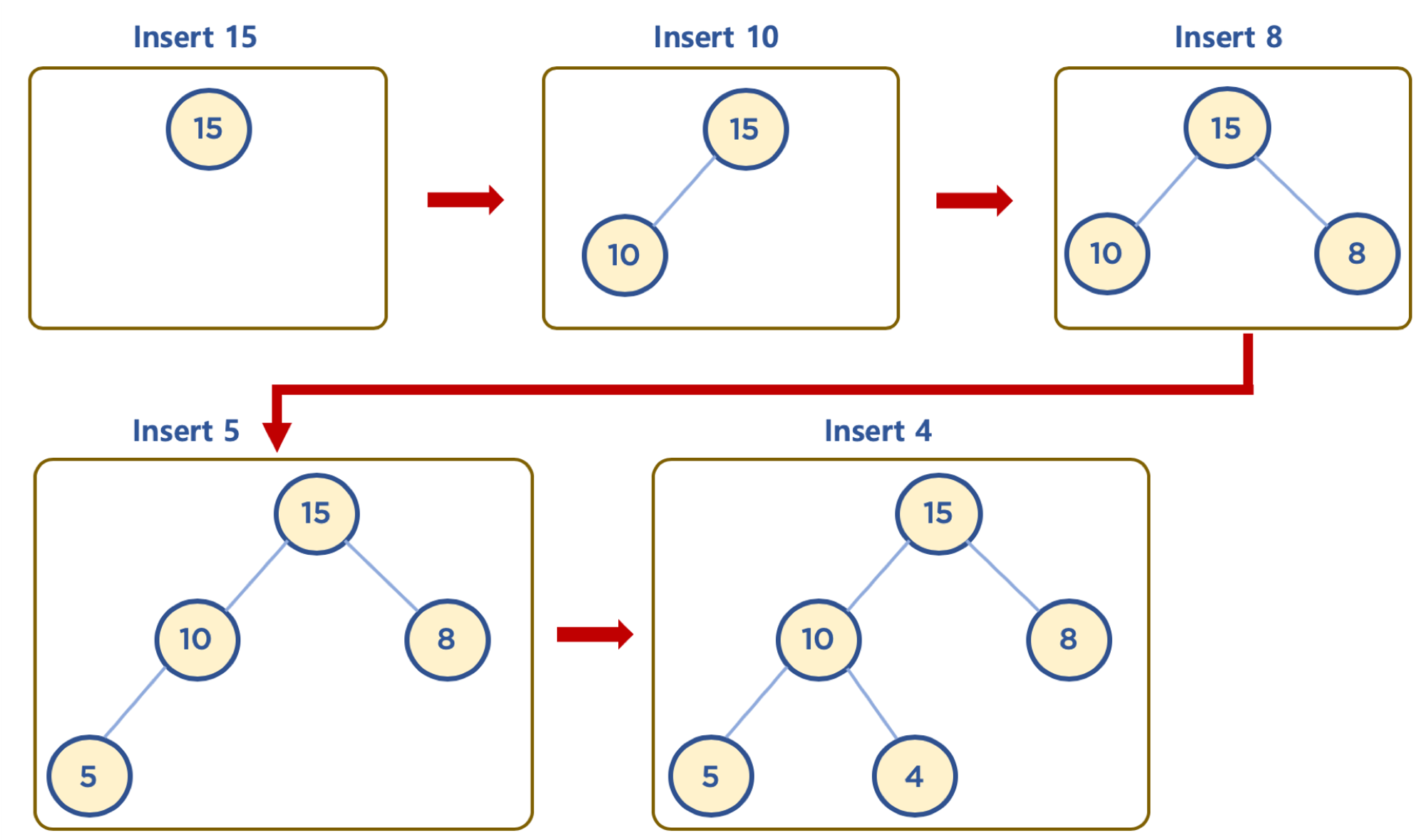
힙에 데이터 삽입
-
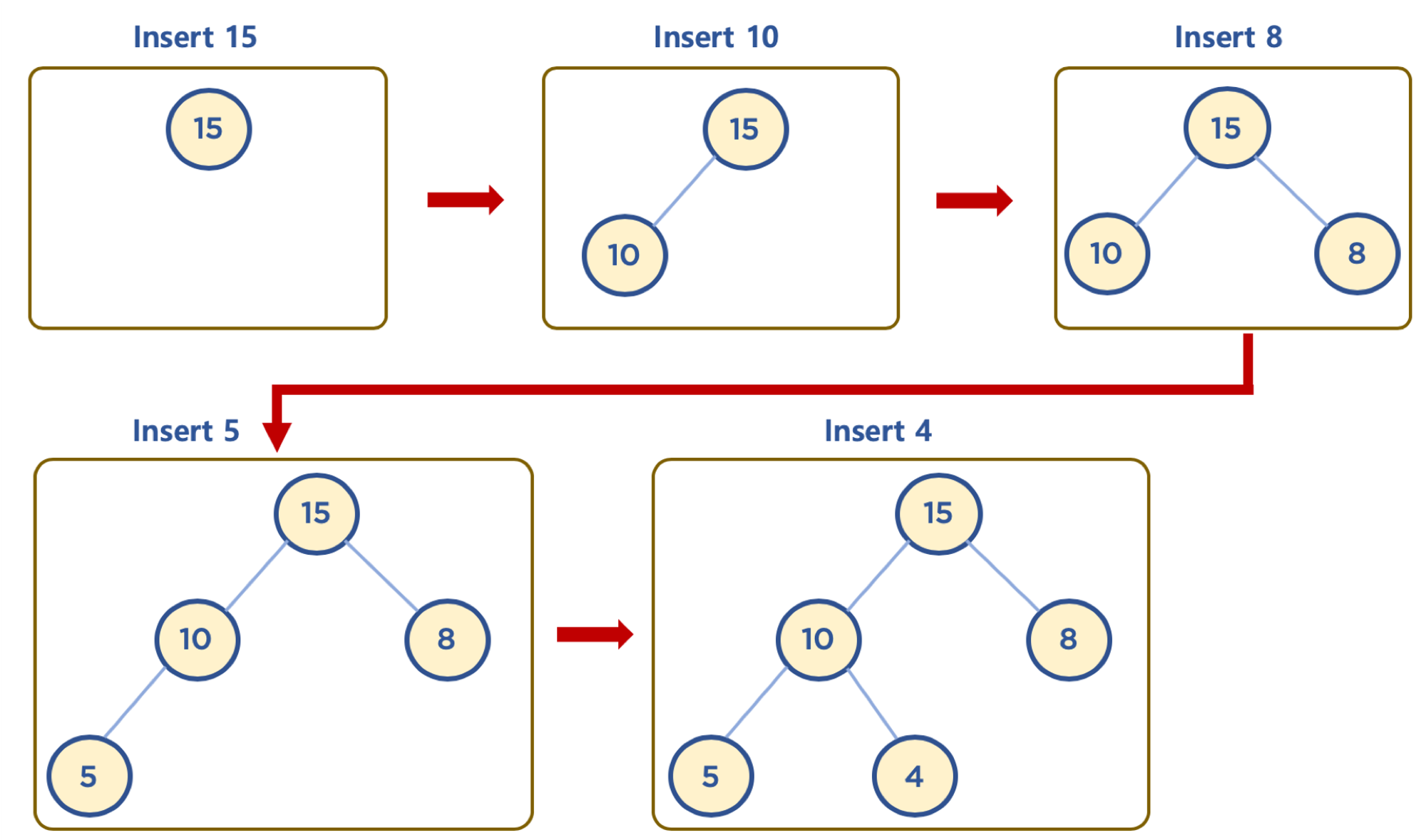
힙은 완전 이진 트리이므로, 삽입할 노드는 기본적으로 왼쪽 최하단부 노드부터 채워지는 형태로 삽입
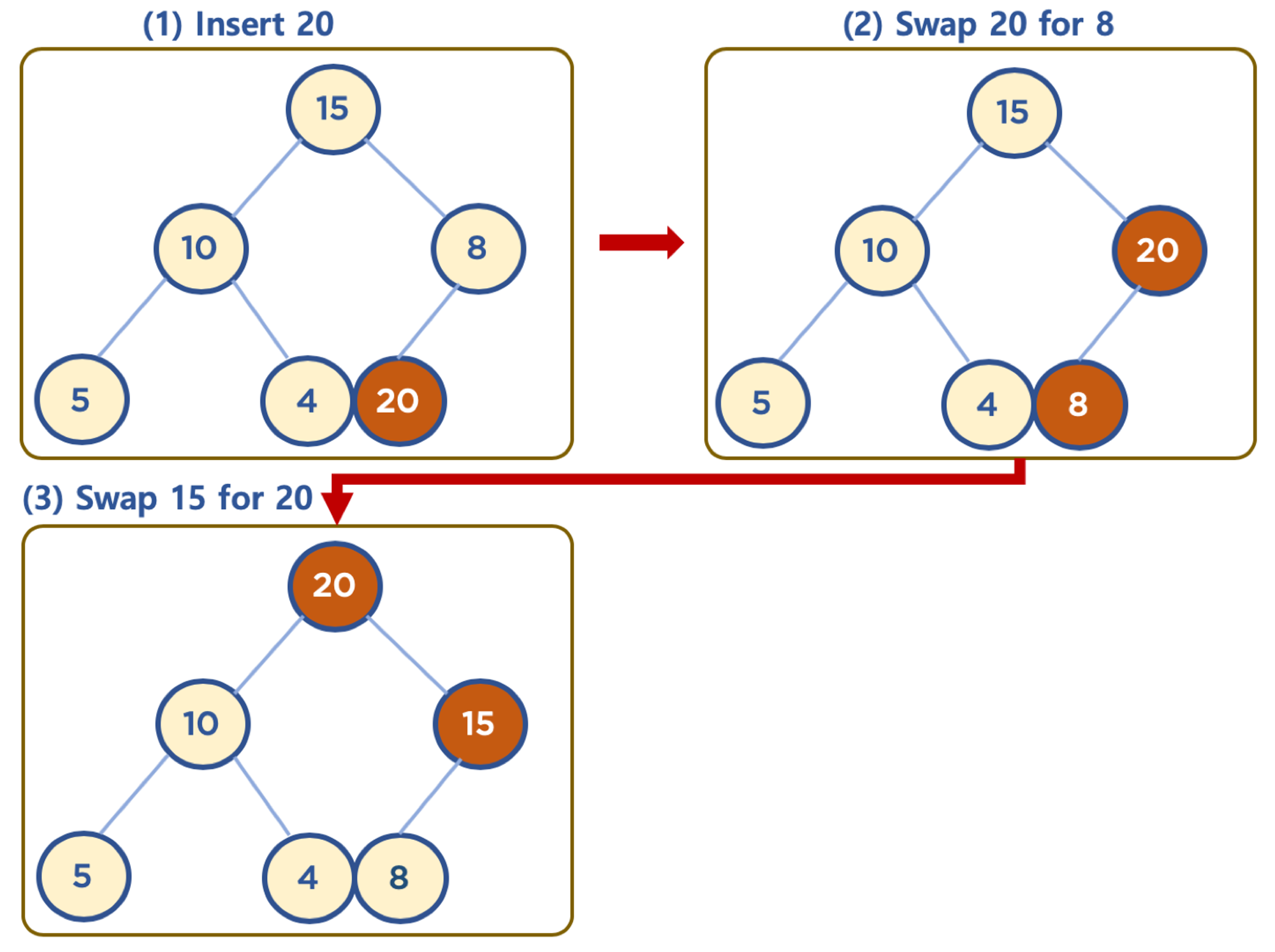
삽입할 데이터가 부모 노드 데이터보다 클 경우 (Max Heap 의 예)
-
먼저 삽입된 데이터는 완전 이진 트리 구조에 맞추어, 최하단부 왼쪽 노드부터 채워짐
-
채워진 노드 위치에서, 부모 노드보다 값이 클 경우, 부모 노드와 위치를 바꿔주는 작업을 반복함 (swap)
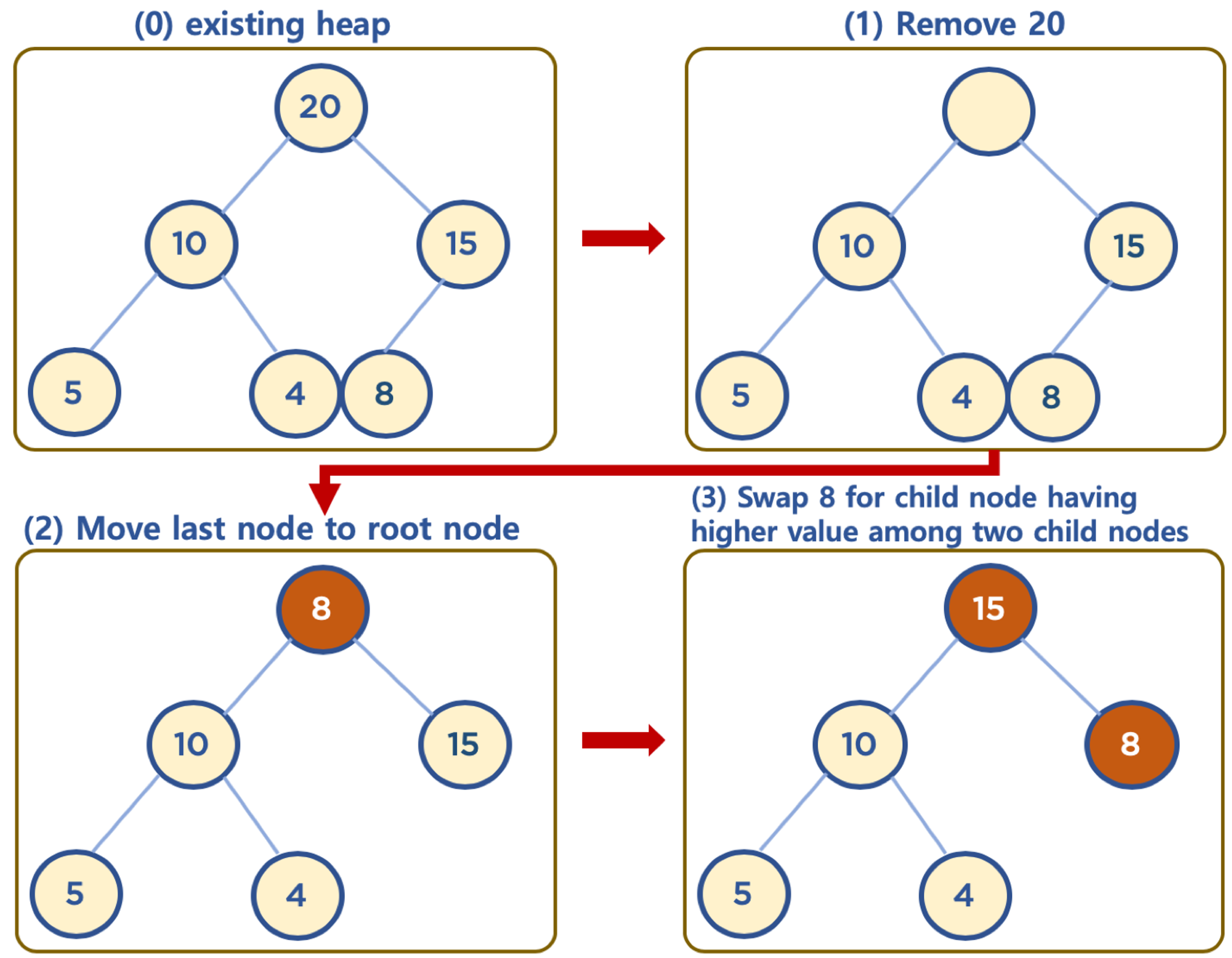
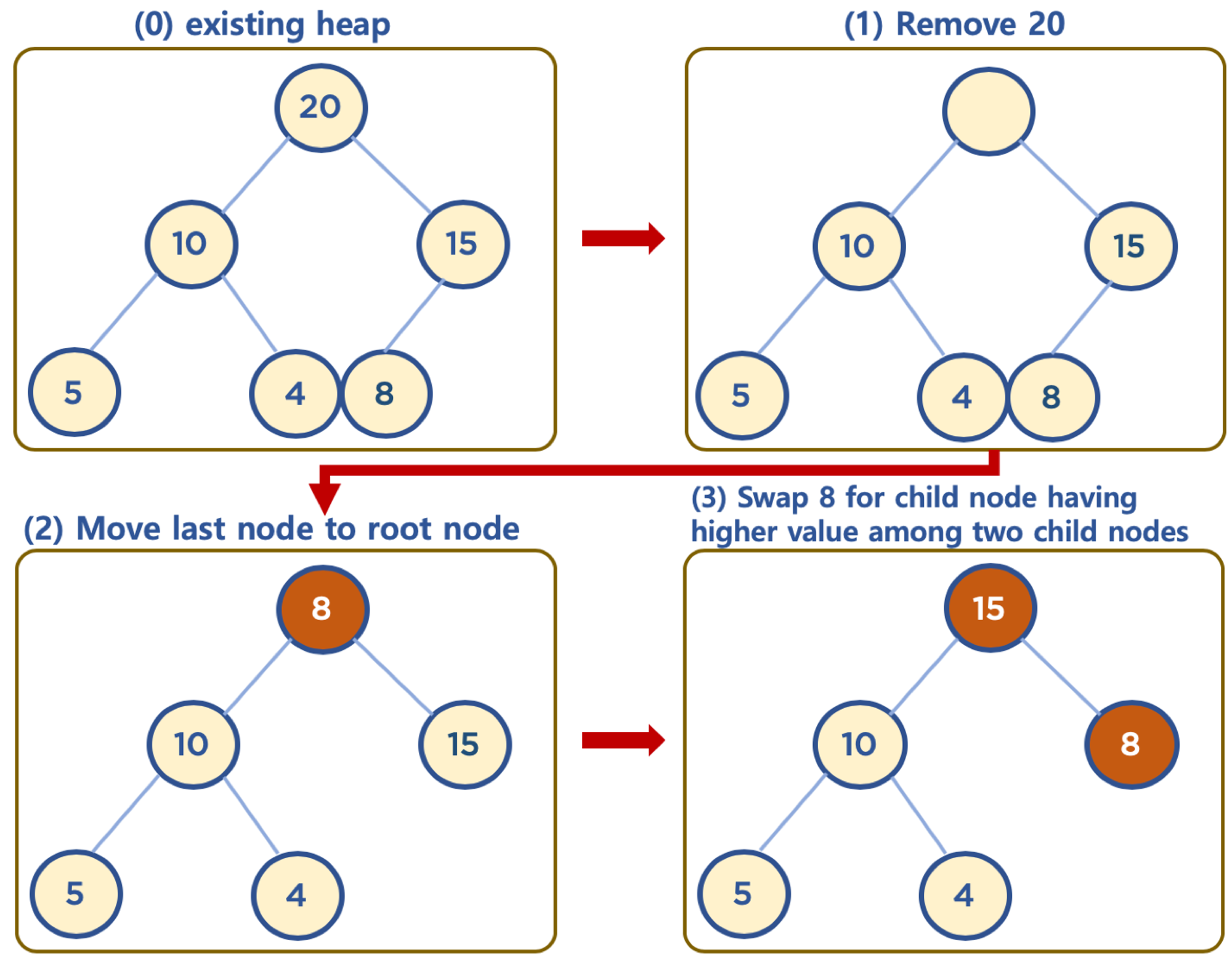
힙의 데이터 삭제하기 (Max Heap 의 예)
-
보통 삭제는 최상단 노드 (root 노드)를 삭제하는 것이 일반적임
- 힙의 용도는 최대값 또는 최소값을 root 노드에 놓아서, 최대값과 최소값을 바로 꺼내 쓸 수 있도록 하는 것임
-
상단의 데이터 삭제시, 가장 최하단부 왼쪽에 위치한 노드 (일반적으로 가장 마지막에 추가한 노드) 를 root 노드로 이동
-
root 노드의 값이 child node 보다 작을 경우, root 노드의 child node 중 가장 큰 값을 가진 노드와 root 노드 위치를 바꿔주는 작업을 반복함 (swap)
-
주요용도
- 우선순위 큐(Priority Queue) : 힙은 우선순위 큐를 구현하는 데 가장 흔히 사용되는 자료구조입니다. 우선순위 큐는 요소들이 우선순위에 따라 정렬되는 추상적 자료형을 말합니다.
- 힙 정렬(Heap Sort) : 힙 자료구조를 이용해서 리스트를 정렬하는 효율적인 알고리즘입니다.
- 그래프 알고리즘 : 다익스트라(Dijkstra's Algorithm)나 프림(Prim's Algorithm)과 같은 그래프 알고리즘에서는 힙이 최소 비용의 노드를 빠르게 찾는데 사용됩니다.
장점
- 힙은 트리 기반의 자료구조이므로 탐색, 삽입, 삭제 연산에 대한 시간 복잡도가 O(log n)입니다. 이는 힙이 크기가 커질수록 이점이 커지는 효율적인 자료구조임을 의미합니다.
- 힙은 최대값(최대 힙의 경우) 또는 최소값(최소 힙의 경우)을 빠르게 찾는데 효율적입니다. 이러한 특성 때문에 우선순위 큐와 같이 최대값 또는 최소값을 빠르게 찾아야 하는 상황에서 힙이 자주 사용됩니다.
단점
- 정렬된 구조가 아님 : 힙은 최대값 또는 최소값만 빠르게 찾을 수 있으며, 이 외의 다른 값들은 정렬되어 있지 않습니다. 따라서 힙은 특정 값의 탐색에 비효율적입니다.
- 임의의 위치에 있는 원소를 삭제하는 연산이 비효율적 : 힙에서 임의의 위치에 있는 원소를 삭제하는 것은 힙의 속성을 유지하기 위해 추가적인 작업이 필요하기 때문에, 이러한 연산은 비효율적입니다.
시간 복잡도
- 삽입: O(log n)
- 삭제: O(log n)
- 최대값/최소값 찾기: O(1)
- 탐색: O(n)
적합한 상황
- 최대값 또는 최소값을 빠르게 찾아야 하는 경우
- 우선순위 큐를 사용해야 하는 경우
- 데이터를 정렬해야 하는 경우 (힙 정렬)
부적합한 상황
- 특정 값의 탐색이 빈번한 경우
- 임의의 위치에 있는 원소를 삭제하는 연산이 빈번한 경우
주의사항
- 힙은 최대값 또는 최소값만 빠르게 찾을 수 있습니다. 따라서 특정 값의 탐색이 필요한 경우에는 힙이 아닌 다른 자료구조를 고려해야 합니다.
- 힙에서 원소를 삽입하거나 삭제할 때는 힙의 속성이 유지되도록 주의해야 합니다. 힙의 속성이 깨지면 힙의 연산이 정상적으로 동작하지 않을 수 있습니다.
구현
힙과 배열
- 일반적으로 힙 구현시 배열 자료구조를 활용함
- 배열은 인덱스가 0번부터 시작하지만, 힙 구현의 편의를 위해, root 노드 인덱스 번호를 1로 지정하면, 구현이 좀더 수월함
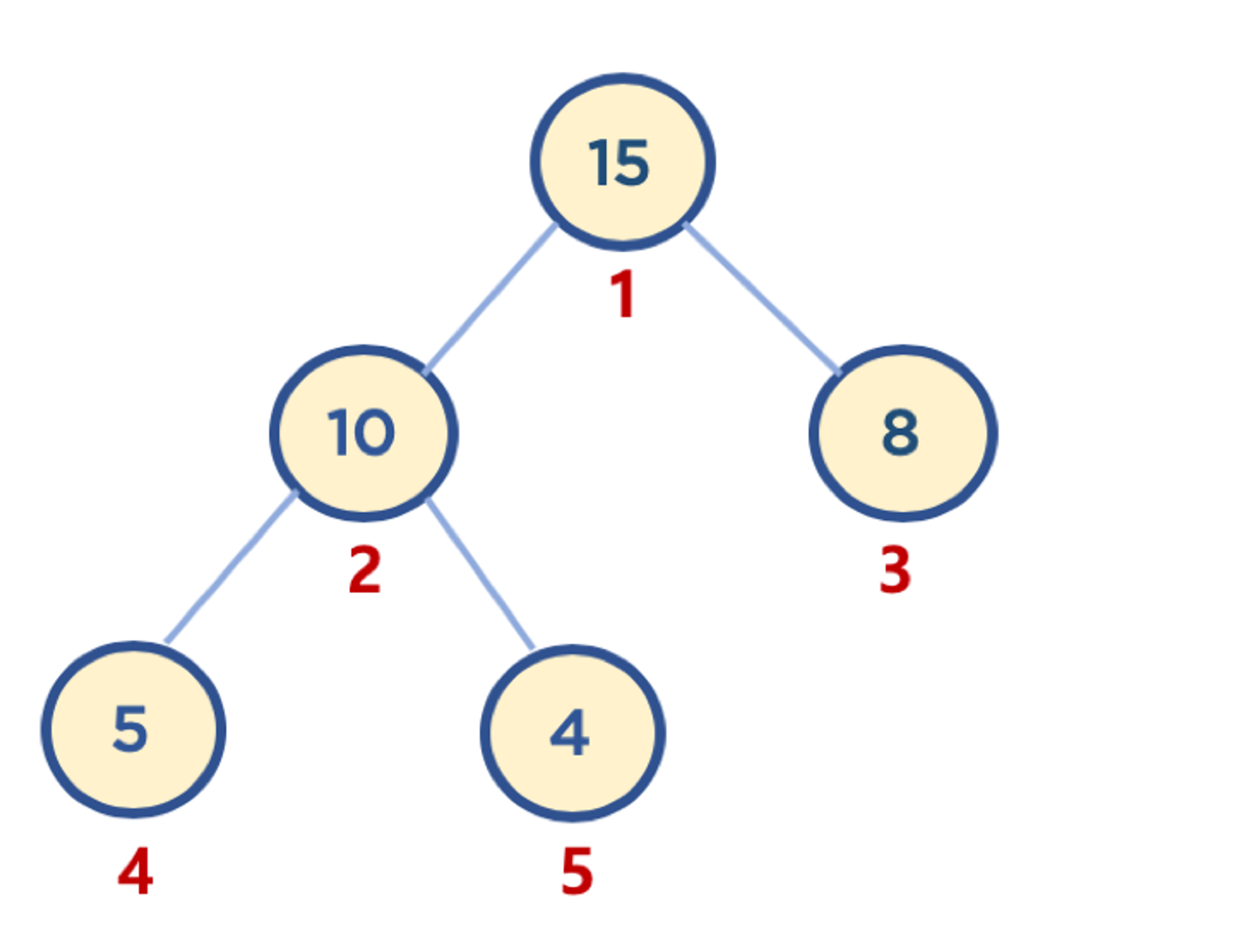
- 부모 노드 인덱스 번호 (parent node's index) = 자식 노드 인덱스 번호 (child node's index) // 2
- 왼쪽 자식 노드 인덱스 번호 (left child node's index) = 부모 노드 인덱스 번호 (parent node's index) * 2
- 오른쪽 자식 노드 인덱스 번호 (right child node's index) = 부모 노드 인덱스 번호 (parent node's index) * 2 + 1
힙에 데이터 삽입 구현 (Max Heap 예)
힙 클래스 구현
class Heap:
def __init__(self, data):
self.heap_array = list()
self.heap_array.append(None)
self.heap_array.append(data)
heap = Heap(1)
heap.heap_array
# [None, 1]- insert
- 인덱스 번호는 1번부터 시작하도록 변경
class Heap:
def __init__(self, data):
self.heap_array = list()
self.heap_array.append(None)
self.heap_array.append(data)
def insert(self, data):
if len(self.heap_array) == 0:
self.heap_array.append(None)
self.heap_array.append(data)
return True
self.heap_array.append(data)
return True- 삽입한 노드가 부모 노드의 값보다 클 경우, 부모 노드와 삽입한 노드 위치를 바꿈
- 삽입한 노드가 루트 노드가 되거나, 부모 노드보다 값이 작거나 같을 경우까지 반복
특정 노드의 관련 노드 위치 알아내기
- 부모 노드 인덱스 번호 (parent node's index) = 자식 노드 인덱스 번호 (child node's index) // 2
- 왼쪽 자식 노드 인덱스 번호 (left child node's index) = 부모 노드 인덱스 번호 (parent node's index) * 2
- 오른쪽 자식 노드 인덱스 번호 (right child node's index) = 부모 노드 인덱스 번호 (parent node's index) * 2 + 1
# 예1 - 10 노드의 부모 노드 인덱스
2 // 2
# 1
# 예1 - 15 노드의 왼쪽 자식 노드 인덱스 번호
1 * 2
# 2
# 예1 - 15 노드의 오른쪽 자식 노드 인덱스 번호
2 * 2 + 1
# 5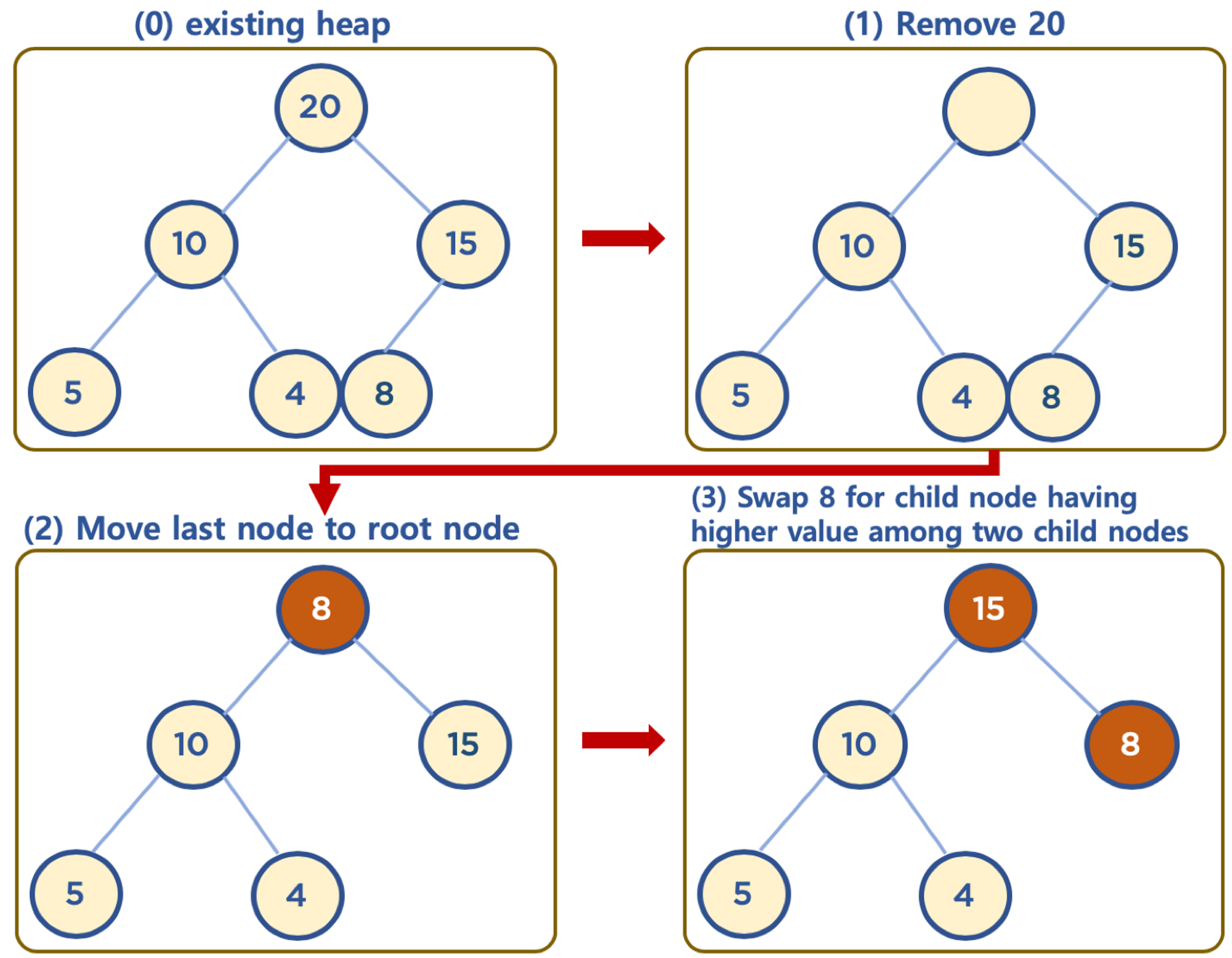
힙에 데이터 삭제 구현 (Max Heap 예)
- 보통 삭제는 최상단 노드 (root 노드)를 삭제하는 것이 일반적임
- 힙의 용도는 최대값 또는 최소값을 root 노드에 놓아서, 최대값과 최소값을 바로 꺼내 쓸 수 있도록 하는 것임
- 상단의 데이터 삭제시, 가장 최하단부 왼쪽에 위치한 노드 (일반적으로 가장 마지막에 추가한 노드) 를 root 노드로 이동
- root 노드의 값이 child node 보다 작을 경우, root 노드의 child node 중 가장 큰 값을 가진 노드와 root 노드 위치를 바꿔주는 작업을 반복함 (swap)
특정 노드의 관련 노드 위치 알아내기
-
부모 노드 인덱스 번호 (parent node's index) = 자식 노드 인덱스 번호 (child node's index) // 2
-
왼쪽 자식 노드 인덱스 번호 (left child node's index) = 부모 노드 인덱스 번호 (parent node's index) * 2
-
오른쪽 자식 노드 인덱스 번호 (right child node's index) = 부모 노드 인덱스 번호 (parent node's index) * 2 + 1
JS
최대 힙
class MaxHeap {
constructor() {
// Initialize heap with null at 0 index
this.heap = [null];
}
// Method to get parent index
getParentIndex(i) {
return Math.floor(i / 2);
}
// Method to get left child index
getLeftChildIndex(i) {
let index = i * 2;
return index < this.heap.length ? index : null;
}
// Method to get right child index
getRightChildIndex(i) {
let index = i * 2 + 1;
return index < this.heap.length ? index : null;
}
// Method to swap two nodes
swap(i1, i2) {
[this.heap[i1], this.heap[i2]] = [this.heap[i2], this.heap[i1]];
}
// Method to get maximum value (root of the heap)
getMax() {
return this.heap[1];
}
// Method to insert a new node
insert(node) {
if (typeof node !== "number") {
return false;
}
this.heap.push(node);
this.bubbleUp();
}
bubbleUp() {
let currentIndex = this.heap.length - 1;
let parentIndex = this.getParentIndex(currentIndex);
/**
* currentIndex > 1 조건은 currentIndex가 "루트 노드 인덱스인 1"보다 커야만 하는 조건입니다.
* 이는 bubbleUp 연산이 루트 노드에 도달했음을 나타내는 중요한 조건입니다.
* 이진 힙에서 부모 노드 인덱스는 항상 자식 노드 인덱스의 나누기 2(소수점 아래를 버림)이므로,
* 루트 노드의 부모 노드는 인덱스 0에 위치하게 됩니다. 인덱스 0에는 어떤 요소도 저장되지 않으므로,
* 만약 currentIndex > 1 조건이 없다면, currentIndex가 1인 경우에도 while 루프가 실행되어 swap 연산이 이루어지게 됩니다.
* 이때 currentIndex는 1, parentIndex는 0이므로, this.heap[1]과 this.heap[0]의 위치가 바뀌게 됩니다.
* 따라서 currentIndex > 1 조건은 루프가 루트 노드를 넘어서서 실행되는 것을 방지하며, 이는 힙의 구조를 유지하는데 중요합니다.
*/
while (
currentIndex > 1 &&
this.heap[parentIndex] < this.heap[currentIndex]
) {
this.swap(currentIndex, parentIndex);
currentIndex = parentIndex;
parentIndex = this.getParentIndex(currentIndex);
}
}
// Method to remove node
remove() {
// 힙의 크기가 1 이하인 경우, 즉 힙에 아무런 요소도 없는 경우에는 null을 반환합니다.
if (this.heap.length <= 1) {
return null;
}
// root 노드를 변수 largest에 저장하고,
let largest = this.heap[1];
// 힙의 마지막 노드를 root 노드의 위치로 이동시킵니다.
const end = this.heap.pop();
// If heap is now empty, set root to null
if (this.heap.length > 1) {
/**
* 힙의 마지막 요소가 루트 노드였다면, pop() 후에 힙은 다시 [null]이 되므로 길이가 1이 됩니다.
* 따라서 if (this.heap.length > 1) 조건문은 힙에 요소가 없는 경우를 피하기 위한 것입니다.
* 이때 this.heap[1] = null; 코드는 사실 필요 없습니다. 왜냐하면 이미 pop()을 수행해서 힙의 마지막 요소는 제거되어 [null]과 같은 구조가 됩니다.
*/
/** 힙 배열에 값이 하나 이상인 경우에만 아래의 this.heap[1] = end 처리가 필요한 이유는
* 만약 힙 배열에 하나의 요소 [null, root]만 있었던 상태에서 pop()을 당했다면 [null]과 같은 결과가 나오기 때문에
* 따로 루트 요소 인덱스에 pop의 결과값을 넣을 필요가 없다.
* 반면 힙배열에 하나 이상의 요소가 남아있다면 루트 노드 위치에 마지막 노드를 업데이트해야 하기 때문이다.
* 즉, [null, 루트노드]와 같은 상황에서 remove()가 호출되었고 this.heap[1] = this.heap.pop()과 같이 처리하였다면
* [null, 루트노드]와 같이 기존 상태 그대로의 결과가 되어 삭제가 되지 않는다.
*/
this.heap[1] = end; // Set the last element to the root
this.bubbleDown();
}
// 마지막으로, 원래의 root 노드였던 largest를 반환합니다.
return largest;
}
bubbleDown() {
// 현재 노드를 가리키는 currentIndex와 그 자식 노드들의 인덱스를 가져옵니다.
let currentIndex = 1;
let leftChildIndex = this.getLeftChildIndex(currentIndex);
let rightChildIndex = this.getRightChildIndex(currentIndex);
// 루프는 왼쪽 자식 노드나 오른쪽 자식 노드 중 하나라도 존재하는 경우 계속됩니다.
while (this.heap[leftChildIndex] || this.heap[rightChildIndex]) {
/**
* 루프 내에서는 먼저 더 큰 자식 노드의 인덱스를 찾습니다.
* 기본적으로 largerChildIndex는 오른쪽 자식 노드의 인덱스로 설정되지만,
* 오른쪽 자식 노드가 존재하지 않거나 왼쪽 자식 노드의 값이 더 큰 경우에는
* largerChildIndex를 왼쪽 자식 노드의 인덱스로 설정합니다.
*/
let largerChildIndex = rightChildIndex;
/**
* JavaScript에서는 0은 falsy 값으로 간주되므로, rightChildIndex가 0인 경우 (!rightChildIndex)가 참이 되어 버립니다.
* 이 때문에, 이진 힙의 루트 노드 (인덱스 1)의 오른쪽 자식 노드 (인덱스 0)에 값이 있다면 해당 노드는 고려되지 않게 됩니다.
* 따라서, !this.heap[rightChildIndex]를 사용하는 것이 더 안전합니다.
* 이렇게 하면 rightChildIndex가 null이거나 undefined일 경우,
* 또는 rightChildIndex가 유효한 인덱스이지만 해당 위치에 노드가 없는 경우를 모두 고려할 수 있습니다
*/
if (
!this.heap[rightChildIndex] ||
this.heap[leftChildIndex] > this.heap[rightChildIndex]
) {
largerChildIndex = leftChildIndex;
}
/**
* 현재 노드의 값과 더 큰 자식 노드의 값을 비교합니다.
* 만약 현재 노드의 값이 더 큰 자식 노드의 값보다 작다면, 둘의 위치를 바꿔줍니다.
* 그리고 currentIndex를 largerChildIndex로 업데이트하고,
* 다음 루프에서 비교할 자식 노드들의 인덱스를 다시 계산합니다.
*/
/**
* while (leftChildIndex !== null || rightChildIndex !== null) 이 구문을 사용하면,
* leftChildIndex 또는 rightChildIndex가 null일 때 this.heap[null]을 참조하게 됩니다.
* 이는 원하지 않는 행동이므로 이를 방지하기 위해 while (this.heap[leftChildIndex] || this.heap[rightChildIndex]) 구문을 사용하는 것입니다.
* while (this.heap[leftChildIndex] || this.heap[rightChildIndex]) 이 조건은 this.heap[leftChildIndex]와 this.heap[rightChildIndex] 중 하나라도
* truthy(참 같은 값)이면 while 루프를 계속 실행하게 됩니다.
* JavaScript에서 null, undefined, 0, NaN, ""(빈 문자열) 등은 모두 falsy(거짓 같은 값)로 평가되기 때문에,
* this.heap[leftChildIndex] 또는 this.heap[rightChildIndex]가 위의 값들 중 하나일 때는 에러 없이 while 루프를 종료하게 됩니다.
* 따라서, while (this.heap[leftChildIndex] || this.heap[rightChildIndex]) 구문을 사용하면,
* leftChildIndex 또는 rightChildIndex가 null인 경우 this.heap[null]을 참조하는 상황을 피할 수 있습니다.
*/
if (this.heap[largerChildIndex] > this.heap[currentIndex]) {
this.swap(currentIndex, largerChildIndex);
currentIndex = largerChildIndex;
leftChildIndex = this.getLeftChildIndex(currentIndex);
rightChildIndex = this.getRightChildIndex(currentIndex);
} else {
// 만약 현재 노드의 값이 더 큰 자식 노드의 값보다 크거나 같다면, 루프를 종료합니다.
break;
}
}
}
printHeap() {
console.log(this.heap);
}
}
let heap = new MaxHeap();
// Insert nodes
heap.insert(3);
heap.insert(2);
heap.insert(1);
heap.insert(7);
heap.insert(8);
heap.insert(4);
heap.insert(10);
heap.insert(16);
heap.insert(12);
heap.printHeap(); // Output: [ null, 16, 12, 10, 7, 8, 3, 1, 2, 4 ]
// Get and print maximum
console.log(heap.getMax()); // Output: 16
// Remove root and print maximum
heap.remove();
console.log(heap.getMax()); // Output: 12
// Remove root and print maximum
heap.remove();
console.log(heap.getMax()); // Output: 10
let heap2 = new MaxHeap();
heap2.insert(5);
heap2.insert(3);
heap2.insert(17);
heap2.insert(10);
heap2.insert(84);
heap2.insert(19);
heap2.insert(6);
heap2.insert(22);
heap2.insert(9);
heap2.printHeap(); // Output: [ null, 84, 22, 19, 10, 3, 17, 6, 5, 9 ]
console.log(heap2.getMax()); // Output: 84
heap2.remove();
console.log(heap2.getMax()); // Output: 22
heap2.remove();
console.log(heap2.getMax()); // Output: 19
heap2.remove();
console.log(heap2.getMax()); // Output: 17
heap2.remove();
console.log(heap2.getMax()); // Output: 10인서트 과정 살펴보기
1단계:
- 3 삽입
- 힙: [null, 3]
- currentIndex: 1
3 - currentIndex > 1은 만족하지 않으므로 while 루프는 실행되지 않습니다.
2단계:
- 2 삽입
- 힙: [null, 3, 2]
- currentIndex: 2
3 / 2 - currentIndex > 1은 만족하지만, heap[getParentIndex(2)] >= heap[2]가 만족하므로 while 루프는 실행되지 않습니다.
3단계:
- 1 삽입
- 힙: [null, 3, 2, 1]
- currentIndex: 3
3
/ \
2 1currentIndex > 1은 만족하지만, heap[getParentIndex(3)] >= heap[3]가 만족하므로 while 루프는 실행되지 않습니다.
4단계:
- 7 삽입
- 힙: [null, 3, 2, 1, 7]
- currentIndex: 4
스왑 전:
3
/ \
2 1
/
7
// currentIndex > 1 && heap[getParentIndex(4)] < heap[4]
// 4 > 1 && 2 < 7
// true
스왑 후 (7과 2 교환):
3
/ \
7 1
/
2
// currentIndex > 1 && heap[getParentIndex(2)] < heap[2]
// 2 > 1 && 3 < 7
// true
스왑 후 (7과 3 교환):
7
/ \
3 1
/
2
// currentIndex > 1 && heap[getParentIndex(1)] < heap[1]
// 1 > 1 && null < 7
// false5단계:
- 8 삽입
- 힙: [null, 7, 3, 1, 2, 8]
- currentIndex: 5
스왑 전:
7
/ \
3 1
/ \
2 8
// currentIndex > 1 && heap[getParentIndex(5)] < heap[5]
// 5 > 1 && 3 < 8
// true
스왑 후 (8과 3 교환):
7
/ \
8 1
/ \
2 3
// currentIndex > 1 && heap[getParentIndex(2)] < heap[2]
// 2 > 1 && 7 < 8
// true
스왑 후 (8과 7 교환):
8
/ \
7 1
/ \
2 3
// currentIndex > 1 && heap[getParentIndex(1)] < heap[1]
// 1 > 1 && null < 8
// false최소 힙
class MinHeap {
constructor() {
this.heap = [null];
}
getMin() {
return this.heap[1];
}
getParentIndex(i) {
return Math.floor(i / 2);
}
getLeftChildIndex(i) {
const index = i * 2;
return index < this.heap.length ? index : null;
}
getRightChildIndex(i) {
const index = i * 2 + 1;
return index < this.heap.length ? index : null;
}
swap(i, j) {
[this.heap[i], this.heap[j]] = [this.heap[j], this.heap[i]];
}
insert(value) {
if (typeof value !== "number") {
return null;
}
this.heap.push(value);
this.bubbleUp();
}
bubbleUp() {
let currentIndex = this.heap.length - 1;
let parentIndex = this.getParentIndex(currentIndex);
while (
currentIndex > 1 &&
this.heap[currentIndex] < this.heap[parentIndex] // 맥스힙과 다른 부분 '>' -> '<'
) {
this.swap(currentIndex, parentIndex);
currentIndex = parentIndex;
parentIndex = this.getParentIndex(currentIndex);
}
}
remove() {
if (this.heap.length <= 1) {
return null;
}
let smallest = this.heap[1];
let end = this.heap.pop(); // Save the result of pop operation to a temporary variable
if (this.heap.length > 1) {
// Check the length again before assigning
this.heap[1] = end; // Set the last element to the root
this.bubbleDown();
}
return smallest;
}
bubbleDown() {
let currentIndex = 1;
let leftChildIndex = this.getLeftChildIndex(currentIndex);
let rightChildIndex = this.getRightChildIndex(currentIndex);
while (this.heap[leftChildIndex] || this.heap[rightChildIndex]) {
let smallestChildIndex = rightChildIndex; // 맥스힙과 다른 부분 largestChildIndex -> smallestChildIndex
if (
!smallestChildIndex ||
this.heap[leftChildIndex] < this.heap[rightChildIndex] //맥스힙과 다른 부분 '>' -> '<'
) {
smallestChildIndex = leftChildIndex;
}
if (this.heap[currentIndex] > this.heap[smallestChildIndex]) {
// 맥스힙과 다른 부분 '<' -> '>'
this.swap(currentIndex, smallestChildIndex);
currentIndex = smallestChildIndex;
leftChildIndex = this.getLeftChildIndex(currentIndex);
rightChildIndex = this.getRightChildIndex(currentIndex);
} else {
break;
}
}
}
printHeap() {
console.log(this.heap);
}
}
let heap = new MinHeap();
heap.insert(3);
heap.insert(2);
heap.insert(1);
heap.insert(7);
heap.insert(8);
heap.insert(4);
heap.insert(10);
heap.insert(16);
heap.insert(12);
heap.printHeap(); // Output: [ null, 1, 2, 3, 7, 8, 4, 10, 16, 12 ]
console.log(heap.getMin()); // Output: 1
heap.remove();
console.log(heap.getMin()); // Output: 2
heap.remove();
console.log(heap.getMin()); // Output: 3Python
heap = Heap(15)
heap.insert(10)
heap.insert(8)
heap.insert(5)
heap.insert(4)
heap.insert(20)
heap.heap_array
# [None, 20, 10, 15, 5, 4, 8]
heap.pop()
# 20
heap.heap_array
# [None, 15, 10, 8, 5, 4] class Heap:
def __init__(self, data):
self.heap_array = list()
self.heap_array.append(None)
self.heap_array.append(data)
def move_down(self, popped_idx):
left_child_popped_idx = popped_idx * 2
right_child_popped_idx = popped_idx * 2 + 1
# case1: 왼쪽 자식 노드도 없을 때
if left_child_popped_idx >= len(self.heap_array):
return False
# case2: 오른쪽 자식 노드만 없을 때
elif right_child_popped_idx >= len(self.heap_array):
if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
return True
else:
return False
# case3: 왼쪽, 오른쪽 자식 노드 모두 있을 때
else:
if self.heap_array[left_child_popped_idx] > self.heap_array[right_child_popped_idx]:
if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
return True
else:
return False
else:
if self.heap_array[popped_idx] < self.heap_array[right_child_popped_idx]:
return True
else:
return False
def pop(self):
if len(self.heap_array) <= 1:
return None
returned_data = self.heap_array[1]
self.heap_array[1] = self.heap_array[-1]
del self.heap_array[-1]
popped_idx = 1
while self.move_down(popped_idx):
left_child_popped_idx = popped_idx * 2
right_child_popped_idx = popped_idx * 2 + 1
# case2: 오른쪽 자식 노드만 없을 때
if right_child_popped_idx >= len(self.heap_array):
if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
self.heap_array[popped_idx], self.heap_array[left_child_popped_idx] = self.heap_array[left_child_popped_idx], self.heap_array[popped_idx]
popped_idx = left_child_popped_idx
# case3: 왼쪽, 오른쪽 자식 노드 모두 있을 때
else:
if self.heap_array[left_child_popped_idx] > self.heap_array[right_child_popped_idx]:
if self.heap_array[popped_idx] < self.heap_array[left_child_popped_idx]:
self.heap_array[popped_idx], self.heap_array[left_child_popped_idx] = self.heap_array[left_child_popped_idx], self.heap_array[popped_idx]
popped_idx = left_child_popped_idx
else:
if self.heap_array[popped_idx] < self.heap_array[right_child_popped_idx]:
self.heap_array[popped_idx], self.heap_array[right_child_popped_idx] = self.heap_array[right_child_popped_idx], self.heap_array[popped_idx]
popped_idx = right_child_popped_idx
return returned_data
def move_up(self, inserted_idx):
if inserted_idx <= 1:
return False
parent_idx = inserted_idx // 2
if self.heap_array[inserted_idx] > self.heap_array[parent_idx]:
return True
else:
return False
def insert(self, data):
if len(self.heap_array) == 1:
self.heap_array.append(data)
return True
self.heap_array.append(data)
inserted_idx = len(self.heap_array) - 1
while self.move_up(inserted_idx):
parent_idx = inserted_idx // 2
self.heap_array[inserted_idx], self.heap_array[parent_idx] = self.heap_array[parent_idx], self.heap_array[inserted_idx]
inserted_idx = parent_idx
return True