Greedy

개념

탐욕 알고리즘(Greedy algorithm)은 각 단계에서 항상 최적의 선택을 하는 방식으로 문제를 해결하는 알고리즘입니다. 이는 현재 상태에서 가장 좋아 보이는 선택을 합니다. 이 선택이 결과적으로 전체 문제의 최적 해답을 주는 경우에 사용됩니다.

• 최적의 해에 가까운 값을 구하기 위해 사용됨

• 여러 경우 중 하나를 결정해야할 때마다, 매순간 최적이라고 생각되는 경우를 선택하는 방식으로 진행해서, 최종적인 값을 구하는 방식

• 감잡기 문제 (동전 문제)

  지불해야 하는 값이 4720원 일 때 1원 50원 100원, 500원 동전으로 동전의 수가 가장 적게 지불하시오.

  • 가장 큰 동전부터 최대한 지불해야 하는 값을 채우는 방식으로 구현 가능

  • 탐욕 알고리즘으로 매순간 최적이라고 생각되는 경우를 선택하면 됨

    function min_coin_count(value, coin_list) {
      let total_coin_count = 0;
      let details = [];
      coin_list.sort((a, b) => b - a); // Sorting in descending order
      for (let coin of coin_list) {
        let coin_num = Math.floor(value / coin); // 몫을 구하여 코인 개수를 구한다
        total_coin_count += coin_num; // 전체 코인수에 합산한다
        value -= coin_num * coin; // 인자로 넘어온 금액에서 차감한다
        details.push([coin, coin_num]); // 결과 리스트에 담는다
      }
      return [total_coin_count, details]; // 전체 코인수와 코인당 개수 정보를 리턴
    }
    
    let coin_list = [1, 100, 50, 500];
    console.log(min_coin_count(4720, coin_list));

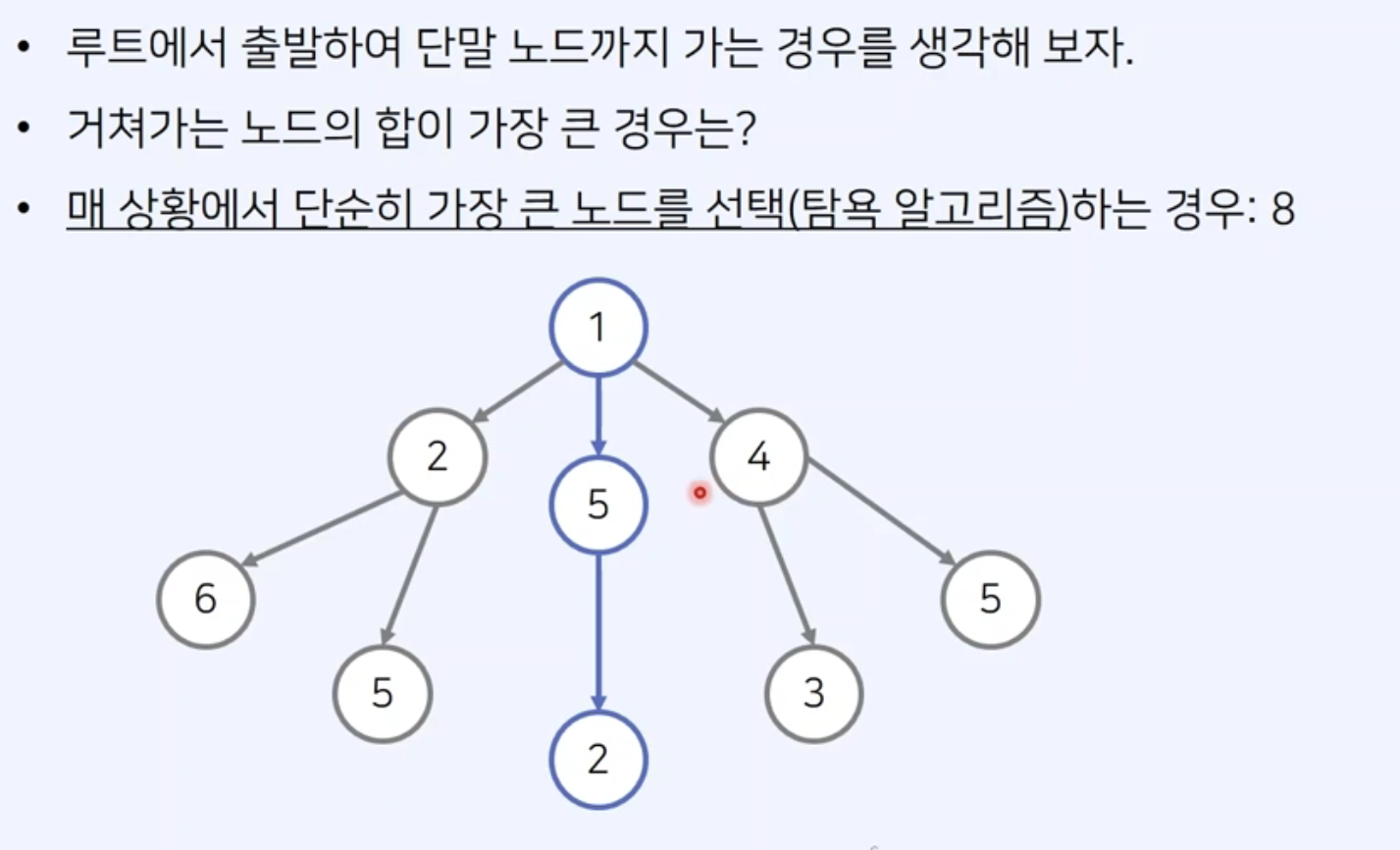
완전 탐색보다 빠르게 근사값을 얻을 수 있으나 단점으로 정답을 찾을 수 없다는 점이있다.

장점

1. 간결성: 탐욕 알고리즘은 간단하고 이해하기 쉽습니다. 각 단계에서 최적의 선택을 하기 때문에, 복잡한 계산이나 처리 없이 간결한 해결책을 찾을 수 있습니다.
2. 시간 효율성: 다른 알고리즘과 비교했을 때, 탐욕 알고리즘은 보통 더 빠른 실행 시간을 보입니다.

단점

1. 최적 해답 보장 안함: 탐욕 알고리즘은 각 단계에서 최선의 선택을 하지만, 이가 반드시 전체 문제에 대한 최적해를 제공한다는 보장은 없습니다. 때문에 탐욕 알고리즘의 적절한 사용은 문제의 특성에 따라 달라집니다.

2. 전체 탐색 불가: 탐욕 알고리즘이 현재 상태에서 최적의 선택을 하기 때문에, 다른 모든 가능한 해를 고려하지 않습니다. 이로 인해 일부 문제에서는 최적 해를 찾지 못할 수 있습니다.

   탐욕 알고리즘의 한계

   • 탐욕 알고리즘은 근사치 추정에 활용할 수 있음

   • 반드시 최적의 해를 구할 수 있는 것은 아니기 때문

   • 탐욕 알고리즘은 최적의 해에 가까운 값을 구하는 방법 중의 하나임

     (물론 탐욕알고리즘에 적합한 문제일 경우 탐욕알고리즘은 문제해결의 좋은 선택지가 될 수 있음, '탐욕적 선택 속성'과 '최적 부분 구조'라는 두 가지 조건이 만족될 때 잘 동작)
     

   • 예)

     

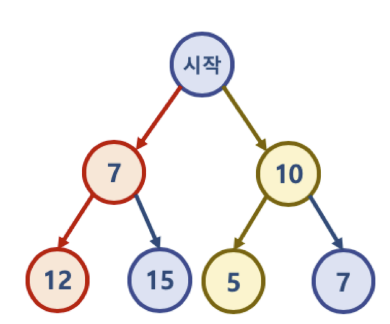
     '시작' 노드에서 시작해서 가장 작은 값을 찾아 leaf node 까지 가는 경로를 찾을 시에 Greedy 알고리즘 적용시 시작 -> 7 -> 12 를 선택하게 되므로 7 + 12 = 19 가 됨, 하지만 실제 가장 작은 값은 시작 -> 10 -> 5 이며, 10 + 5 = 15 가 답

사용에 적합한 상황

탐욕 알고리즘은 '탐욕적 선택 속성'과 '최적 부분 구조'라는 두 가지 조건이 만족될 때 잘 동작합니다. 즉, 현재의 최선의 선택이 전체 문제에 대한 최적 해답에 포함되고, 큰 문제의 최적 해답이 작은 부분 문제들의 최적 해답으로 구성되는 경우에 탐욕 알고리즘이 잘 동작합니다. 예를 들어, 최소 신장 트리 문제, 하프만 코딩, Dijkstra의 알고리즘 등이 있습니다.

사용에 부적합한 상황

탐욕 알고리즘은 각 단계에서의 최적의 선택이 전체 문제의 최적 해답을 구성하지 않는 경우, 즉 '탐욕적 선택 속성'과 '최적 부분 구조'가 만족되지 않는 경우에는 잘 동작하지 않습니다. 예를 들어, 0-1 배낭 문제, 여행하는 판매원 문제(TSP) 등에서는 탐욕 알고리즘이 최적의 해답을 구하지 못할 수 있습니다.

주의사항

탐욕 알고리즘을 사용할 때는 해당 문제가 탐욕 알고리즘을 사용해서 최적 해답을 구할 수 있는 문제인지를 먼저 확인해야 합니다. 그렇지 않다면, 탐욕 알고리즘은 최적 해답을 제공하지 못하고 불완전하거나 부정확한 결과를 출력할 수 있습니다.

시간복잡도

탐욕 알고리즘의 시간 복잡도는 문제에 따라 다르지만, 일반적으로 다른 알고리즘보다 더 효율적입니다. 탐욕 알고리즘이 각 단계에서 최적의 선택을 하기 때문에, 모든 가능성을 탐색하는 것보다 더 빠른 실행 시간을 가질 수 있습니다.

관련 문제

• 부분 배낭 문제 (Fractional Knapsack Problem)

  무게 제한이 k인 배낭에 최대 가치를 가지도록 물건을 넣는 문제

  • 각 물건은 무게(w)와 가치(v)로 표현될 수 있음

  • 물건은 쪼갤 수 있으므로 물건의 일부분이 배낭에 넣어질 수 있음, 그래서 Fractional Knapsack Problem 으로 부름

    (Fractional Knapsack Problem 의 반대로 물건을 쪼개서 넣을 수 없는 배낭 문제도 존재함 (0/1 Knapsack Problem 으로 부름)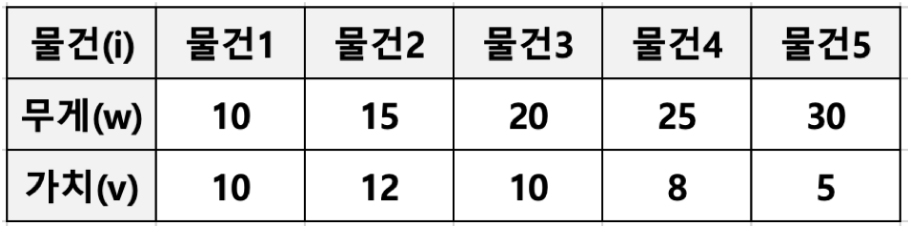

    

    function get_max_value(data_list, capacity) {
      // 무게분의 가치로 정렬
      data_list.sort((a, b) => b[1] / b[0] - a[1] / a[0]);
    
      let total_value = 0;
      let details = [];
    
      for (let data of data_list) {
        if (capacity - data[0] >= 0) {
          // 배낭에 무게가 남았다면
          capacity -= data[0];
          total_value += data[1];
          details.push([data[0], data[1], 1]);
        } else {
          // 배낭에 물건 1개를 담을 수 없는 경우
          // 물건을 쪼갠다
          let fraction = capacity / data[0];
          total_value += data[1] * fraction;
          details.push([data[0], data[1], fraction]);
          break;
        }
      }
      return [total_value, details];
    }
    
    let data_list = [
      [10, 10],
      [15, 12],
      [20, 10],
      [25, 8],
      [30, 5],
    ];
    console.log(get_max_value(data_list, 30));

• ATM 문제

  11399번: ATM

      function minTotalWaitingTime(N, P) {
          P.sort((a, b) => a - b);
          let totalWaitingTime = 0;
          for (let i = 0; i < N; i++) {
              totalWaitingTime += P[i] * (N - i);
          }
          return totalWaitingTime;
      }
  
      // Usage:
      let N = 5;
      let P = [3, 1, 4, 3, 2];
      console.log(minTotalWaitingTime(N, P));  // Output: 32

• 강의실 문제