개념
최소 신장 트리(Minimum Spanning Tree, MST)는 가중치가 할당된 무향 그래프에서 모든 노드를 연결하는데 필요한 간선들의 가중치의 합이 최소가 되는 트리를 의미합니다. 신장 트리는 그래프의 모든 노드를 포함하는 트리이며, 최소 신장 트리는 그 중에서 간선의 가중치 합이 최소인 트리를 선택하는 것입니다. 이를 구하는 대표적인 알고리즘으로는 Prim's 알고리즘과 Kruskal's 알고리즘이 있습니다.
신장트리 (Spanning Tree)
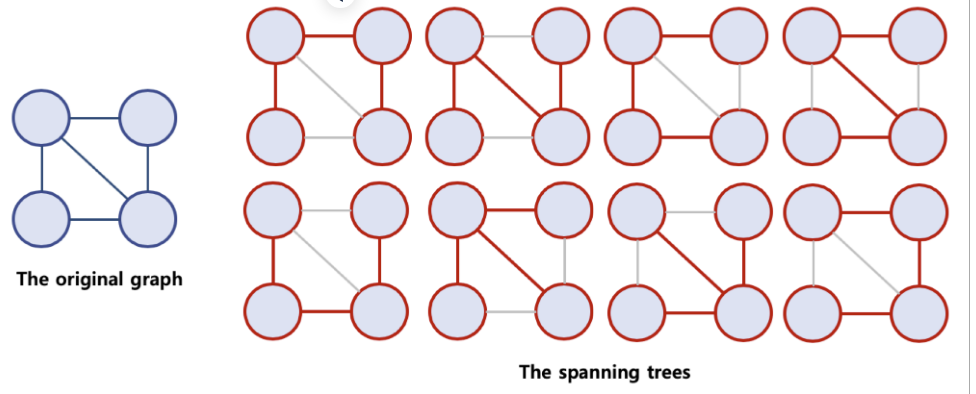
- 신장 트리의 조건
- 본래의 그래프의 모든 노드를 포함해야 함
- 모든 노드가 서로 연결
- 트리의 속성을 만족시킴
- 사이클이 존재하지 않음
최소신장트리
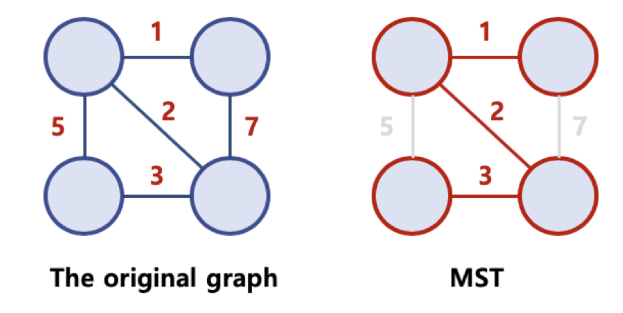
- Minimum Spanning Tree, MST 라고 불리움
- Spanning Tree 중에서, 간선의 가중치 합이 최소인 Spanning Tree를 지칭함
최소신장트리 알고리즘
최소신장트리를 찾을 수 있는 알고리즘은 대표적으로 크루스칼, 프림 알고리즘이 존재함
장점
최소 신장 트리는 네트워크 구축 비용 최소화, 물자 배송, 전력 공급 등 다양한 실생활 문제를 해결하는 데 사용될 수 있습니다. 또한 그래프의 복잡성을 줄이면서도 그래프의 주요 연결 패턴을 보존할 수 있어 데이터 압축이나 그래프 시각화에도 유용합니다.
단점
최소 신장 트리는 간선의 가중치만을 고려하기 때문에, 그래프의 특정 특성이나 요구 사항을 고려하지 못할 수 있습니다. 또한, 최소 신장 트리가 유일하지 않을 경우가 있으며, 이런 상황에서는 어떤 트리가 '최선'인지 결정하기 어렵습니다.
사용에 적합한 상황
최소 신장 트리는 그래프의 모든 노드를 최소 비용으로 연결해야 하는 상황에 적합합니다. 예를 들어, 도시 간 도로 건설, 컴퓨터 네트워크 설계, 전력선 설치 등의 문제에서는 모든 지점을 연결하는 최소 비용의 솔루션을 찾는 것이 중요합니다.
사용에 부적합한 상황
최소 신장 트리는 각 노드 간의 최단 경로를 찾는 문제에는 적합하지 않습니다. 또한, 그래프에 방향성이 있거나 노드 간의 연결성보다 노드나 간선의 특정 특성을 더 중요하게 여기는 상황에서는 최소 신장 트리가 적절한 해결책이 아닐 수 있습니다.
주의사항
최소 신장 트리를 구할 때는 그래프에 사이클이 없도록 주의해야 합니다. 최소 신장 트리는 모든 노드를 포함하는 트리이므로 사이클을 형성하면 안 됩니다. 또한, 최소 신장 트리는 가중치가 할당된 무향 그래프에만 적용할 수 있으므로, 그래프의 성질을 잘 이해하고 알고리즘을 적용해야 합니다.
시간 복잡도
- Kruskal's 알고리즘: O(E log E)
- Prim's 알고리즘: O(E log V)
여기서 E는 그래프의 간선의 수, V는 노드의 수를 나타냅니다. Kruskal's 알고리즘은 모든 간선을 정렬하는 데 O(E log E)의 시간이 걸리며, Prim's 알고리즘은 우선순위 큐를 사용하여 각 노드를 처리하는 데 O(E log V)의 시간이 걸립니다.