유니온 파인드 알고리즘

개념

DSU(Disjoint Set Union)라고도 하는 Union-Find 알고리즘은 각각의 부분 집합에서 특정 요소가 중복이되지 않는지 체크하기 위해서 사용됩니다. (유니온 파인드 알고리즘은 크루스크칼 알고리즘에서도 사용되는데 이때는 사이클이 생기지 않는지를 확인하기 위해 사용되기도 합니다.) 크게 찾기, 합치기 두 가지 주요 작업을 지원합니다.

Disjoint Set이란

• 서로 중복되지 않는 부분 집합들로 나눠진 원소들에 대한 정보를 저장하고 조작하는 자료구조
• 공통 원소가 없는 (서로소) 상호 배타적인 부분 집합들로 나눠진 원소들에 대한 자료구조를 의미함
• Disjoint Set = 서로소 집합 자료구조

1. Find: 특정 요소가 속한 하위 집합을 결정합니다. 두 요소가 동일한 하위 집합에 있는지 확인하는 데 사용할 수 있습니다.
2. Union: 두 개의 하위 집합을 단일 하위 집합으로 결합합니다.

이러한 작업은 종종 그래프 알고리즘에서 두 노드가 동일한 구성 요소에 연결되어있는지 여부를 빠르게 확인하고 두 구성 요소를 하나로 결합하는 데 사용됩니다. 즉, 노드들 중에 연결된 노드를 찾거나, 노드들을 서로 연결할 때 (합칠 때) 사용합니다.

Disjoint Set을 만들때도 사용되며 크루스칼 알고리즘에서 사이클을 체크할때도 사용됩니다.

유니온 파인드 알고리즘의 프로세스

1. 초기화

   

   • n 개의 원소가 개별 집합으로 이뤄지도록 초기화

2. Union

   

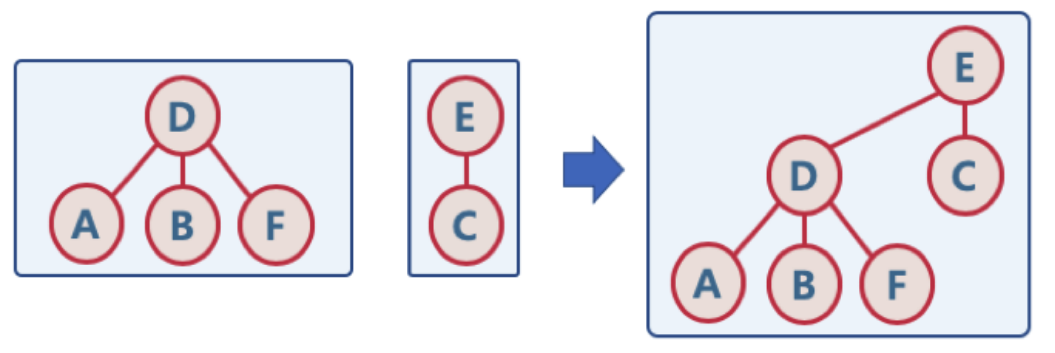
   • 각각의 노드에 간선을 연결하는 작업
   • 두 개별 집합을 하나의 집합으로 합침
   • 두 트리를 하나의 트리로 만듬

3. Find

   

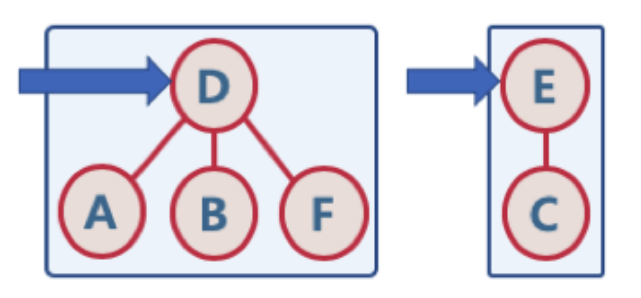
   • 사이클을 체크
   • 여러 노드가 존재할 때, 두 개의 노드를 선택해서, 현재 두 노드가 서로 같은 그래프에 속하는지 판별하기 위해, 각 그룹의 최상단 원소 (즉, 루트 노드)를 확인
   • 두 노드를 연결할때 각각의 노드의 루트 노드를 체크해서 루트노드가 동일하다면 연결시 사이클이 발생함을 알 수 있다.

   크루스칼 알고리즘에서는 간선을 연결할때 유니온을 사용하고 선택한 간선으로 인하여 사이클이 생기는지를 체크할때는 파인드를 사용한다.

최악의 경우의 Union-Find 알고리즘

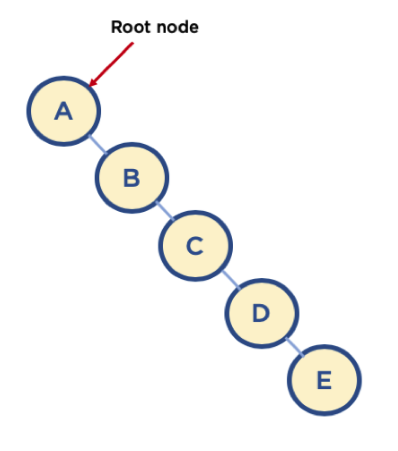
최악의 경우 위의 이미지와 같이 높이만 깊은 트리가 있다면 파인드 / 유니온을 처리할때 링크드 리스트의 맨 끝단을 찾아가는것 같은 선형적인 시간복잡도를 갖게된다.

이와 같은 상황에서는 Find/Union시 계산량이 O(N) 이 될 수 있으므로, 해당 문제를 해결하기 위해, union-by-rank, path compression 기법을 사용한다.

유니온 바이 랭크나 패스 컴프레션은 트리의 높이를 최대한 낮춰 루트노드를 빠르게 찾을 수 있게끔하는 기법이다.

union-by-rank 기법

유니온 바이 랭크 기법의 목적은 두 개의 부분집합이 합쳐질때 어떻게하면 높이를 작게하느냐에 초점을 맞췄다고 볼 수 있다.

각 트리에 대해 높이(rank)를 기억해 두고,Union시

Case1) 두 트리의 높이(rank)가 다르면, 높이가 작은 트리를 높이가 큰 트리에 붙인다.

즉, 높이가 큰 트리의 루트 노드가 두 트리의 루트 노드가 되게 하여 결과적으로 트리의 높이를 가장 작게 만들 수 있다.

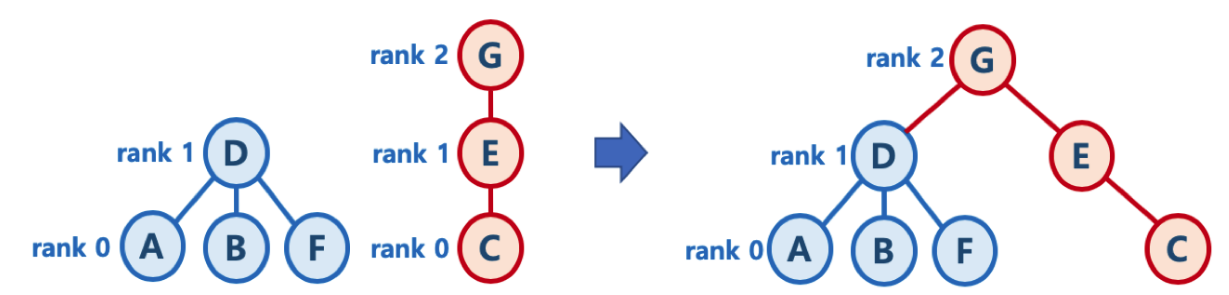
만약 두 그래프를 합칠때 C노드에 D노드를 붙이게되면 Union/Find시 시간 복잡도가 높아지게된다.

Case2) 만약 두 트리의 높이가 같다면 한쪽 트리의 루트노드 랭크를 1 증가시키고 이 루트 노드에 다른 트리의 루트 노드를 연결한다.

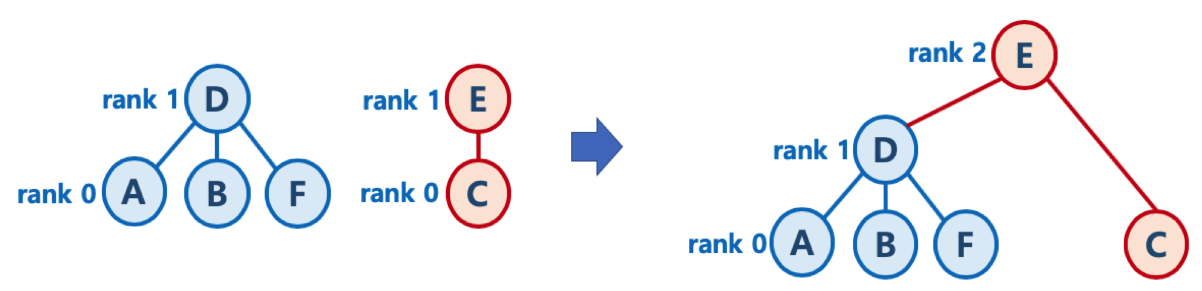
루트 노드의 랭크만 증가시키는 것은 트리의 높이가 실제로 증가했음을 반영하는 것입니다. 이 때문에 루트 노드가 아닌 다른 노드들의 랭크를 증가시킬 필요가 없습니다. 그 노드들의 랭크는 그 노드를 루트로 하는 서브트리의 높이를 나타내기 때문이죠.

하위 노드들의 랭크를 갱신하지 않아도 되는 또 다른 이유는 "파인드(find)" 연산을 수행할 때 경로 압축(path compression)이라는 기법을 사용하기 때문입니다. 이 기법은 파인드 연산을 수행하면서 만난 모든 노드를 바로 루트에 연결하는 방식으로, 이로 인해 실제 트리의 높이가 랭크보다 낮아질 수 있습니다. 이 경우, 각 노드의 랭크를 그 노드를 루트로 하는 트리의 실제 높이로 갱신하려면 불필요하게 많은 연산이 필요하게 됩니다.

초기화시, 모든 원소는 높이(rank)가 0인 개별 집합인 상태에서 하나씩 원소를 합칠(Union)때, union-by-rank 기법을 사용하면 최악의 트리 구조 상황과 비교하였을때 union 작업과 find 작업 모두의 시간복잡도 O(N)을 O(logN)으로 낮출 수 있습니다.

1. Union 작업: 어떠한 최적화도 없다면, union 작업은 단순히 한 트리를 다른 트리 아래에 붙이는 작업으로, 이는 매우 불균형한 트리를 만들어낼 수 있고 최악의 경우 시간 복잡도가 O(N)이 됩니다. union-by-rank 최적화를 사용하면, 더 작은 rank (기본적으로 트리의 크기에 대한 휴리스틱)를 가진 트리가 더 큰 rank를 가진 트리의 루트 아래에 붙게 됩니다. 만약 rank가 같다면, 루트 중 하나가 임의로 선택되지만 그 rank는 1만큼 증가합니다. 이 과정은 트리가 상대적으로 균형을 유지하도록 보장하며, 최악의 경우 시간 복잡도를 O(logN)으로 줄입니다.
2. Find 작업: 어떠한 최적화도 없다면, find 작업은 단순히 부모 포인터를 따라 루트를 찾는 작업으로, 불균형한 트리에 대해 최악의 경우 시간 복잡도는 O(N)이 됩니다. union-by-rank 최적화를 사용하면, 트리가 상대적으로 균형을 유지되므로 모든 노드의 깊이 (즉, 루트에 도달하기 위한 점프 수)는 최대 logN이므로, find 작업의 시간 복잡도가 O(logN)으로 줄어듭니다.

**path compression**

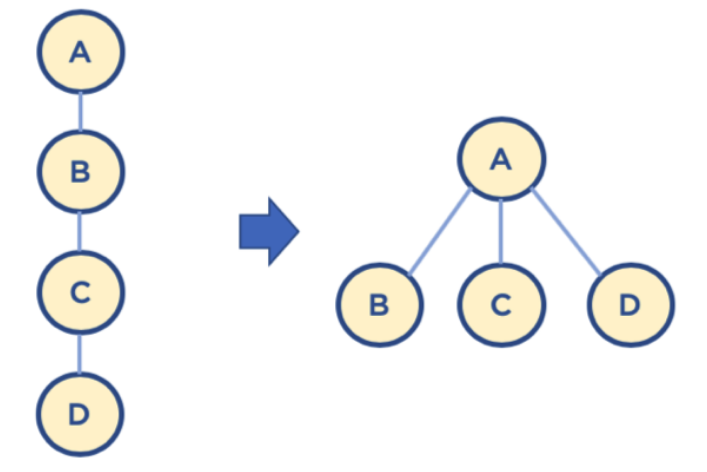
경로 압축 기법은 Find를 실행할때 동작을 한다.

• Find는 루트 노드를 찾는다.
• Find를 실행한 노드에서 거쳐간 노드를 루트 노드에 다이렉트로 연결한다.
• 따라서 Find를 실행한 노드는 이후부터는 루트 노드를 한번에 알 수 있다.

union-by-rank와 path compression 기법을 함께 사용시의 시간 복잡도

union-by-rank와 path compression 기법을 함께 사용할 경우 다음 계산식을 만족함이 수학적으로 증명되었다고한다.

• 𝑂(𝑀𝑙𝑜𝑔∗𝑁)
• 𝑙𝑜𝑔∗𝑁 은 다음 값을 가짐이 증명됨

  • N이  2^65536값을 가지더라도,  log*N의 값이 5의 값을 가지므로, 거의 O(1), 즉 상수값에 가깝다고 볼 수 있다고 한다.

    N	𝑙𝑜𝑔∗𝑁
    1	0
    2	1
    4	2
    16	3
    65536	4
    265536265536	5

장점

1. 효율성: Union-Find 알고리즘은 거의 일정한 시간 연산을 사용하는 분리 집합 연산에 매우 효율적일 수 있습니다.
2. 단순성: 알고리즘은 상대적으로 간단하고 구현하기 쉽습니다.
3. 다재다능성: Union-Find 알고리즘은 Kruskal 알고리즘, 무방향 그래프의 순환 감지 등과 같은 다른 많은 알고리즘에서 사용됩니다.

단점

1. 추가 공간: Union-Find 알고리즘은 집합을 저장하기 위해 배열을 사용하기 때문에 데이터 저장을 위한 추가 공간이 필요합니다.
2. 경로 압축 최적화는 선택 사항입니다: 경로 압축은 효율성을 크게 향상시킬 수 있지만 선택 사항이며 구현하지 않으면 비효율적인 작업이 발생할 수 있습니다.

사용에 적절한 상황

Union-Find 알고리즘은 서로소 집합이 여러 개인 경우에 적합하며 요소가 특정 집합에 속하는지 확인하거나 두 집합을 병합하려는 경우에 적합합니다. 네트워크 연결, 이미지 처리, 그래프에서 주기 찾기와 같은 상황에서 매우 유용합니다.

사용에 부적절한 상황

Union-Find 알고리즘은 find 및 union 이외의 작업을 수행해야 하는 상황에는 적합하지 않습니다. 요소 검색, 요소 삭제 또는 세트의 요소 반복을 위한 것이 아닙니다.

주의

초기에 하나의 요소로 각 집합을 초기화하는 것이 중요하며 알고리즘이 효율적이려면 찾기 작업에서 경로 압축을 수행해야 합니다.

시간 복잡도

알고리즘의 시간 복잡도는 유니온바이랭크 및 패스 컴프레션 기법에 의한 합집합을 사용하는 경우 연산에 대해 거의 O(1)입니다.

구현

class UnionFind {
  constructor(n) {
    this.parent = Array(n).fill().map((_, i) => i); // 초기에는 모든 원소들이 자기 자신을 부모로 가집니다
    this.rank = Array(n).fill(0); // 모든 노드의 랭크를 0으로 초기화합니다
  }

  find(x) {
    if (this.parent[x] !== x) {
      // 경로 압축: 경로에 있는 각 노드를 루트로 가리키도록 합니다
      this.parent[x] = this.find(this.parent[x]);
    }
    return this.parent[x];
  }

  union(x, y) {
    let xRoot = this.find(x); // x의 루트를 찾습니다
    let yRoot = this.find(y); // y의 루트를 찾습니다

    // 만약 같은 집합에 속해 있다면, 합칠 필요가 없습니다
    if (xRoot === yRoot) return;

    // 랭크에 의한 유니온:
    if (this.rank[xRoot] > this.rank[yRoot]) {
      // x의 랭크가 y의 랭크보다 높다면, y의 루트를 x로 합니다
      this.parent[yRoot] = xRoot;
    } else if (this.rank[xRoot] < this.rank[yRoot]) {
      // y의 랭크가 x의 랭크보다 높다면, x의 루트를 y로 합니다
      this.parent[xRoot] = yRoot;
    } else {
      // 랭크가 같다면, 하나를 루트로 지정하고 그 랭크를 1 증가시킵니다
      this.parent[yRoot] = xRoot;
      this.rank[xRoot]++;
    }
  }
}

let uf = new UnionFind(5); // {0}, {1}, {2}, {3}, {4}

uf.union(0, 1); // {0, 1}, {2}, {3}, {4}
console.log(uf.find(0) === uf.find(1)); // true
console.log(uf.find(0) !== uf.find(2)); // true

uf.union(2, 3); // {0, 1}, {2, 3}, {4}
console.log(uf.find(2) === uf.find(3)); // true

uf.union(0, 2); // {0, 1, 2, 3}, {4}
console.log(uf.find(0) === uf.find(3)); // true
console.log(uf.find(3) !== uf.find(4)); // true

uf.union(0, 4); // {0, 1, 2, 3, 4}
console.log(uf.find(1) === uf.find(4)); // true