Tree

트리 자료구조는 계층적인 구조를 갖는 데이터를 표현하기 위한 자료구조입니다. 트리는 노드(node)들과 그 노드들을 연결하는 간선(edge)들로 구성되어 있습니다. 각 노드는 값을 저장하며, 간선은 노드 간의 관계를 나타냅니다. 트리는 다음과 같은 특징을 갖습니다.

Node: 트리에서 데이터를 저장하는 기본 요소

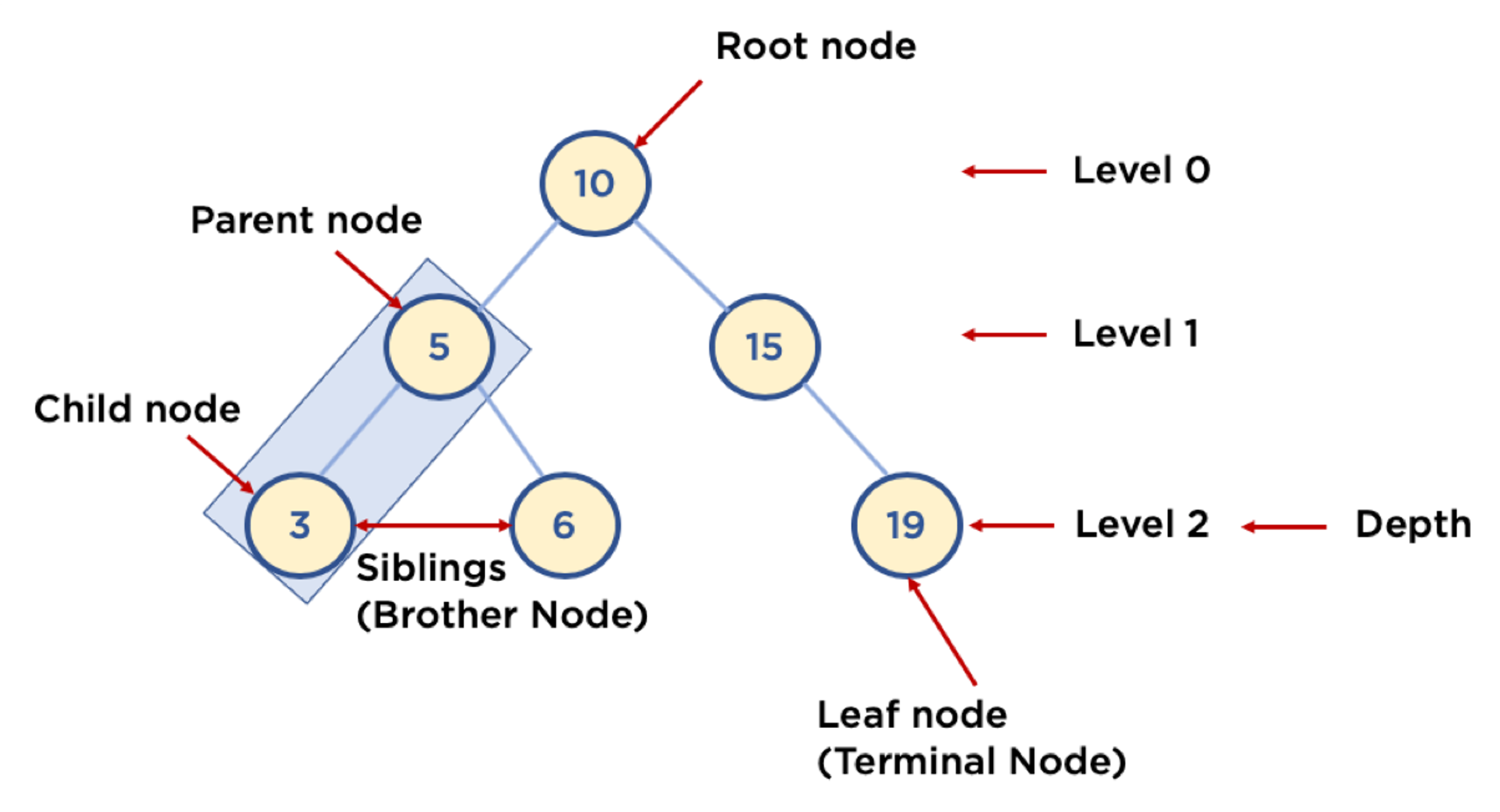
1. 루트(root) 노드: 트리의 최상위 노드로, 부모가 없는 노드입니다.
2. 부모(parent) 노드: 다른 노드를 자식으로 갖는 노드입니다.
3. 자식(child) 노드: 부모 노드에 연결된 노드입니다.
4. 잎(leaf) 노드: 자식이 없는 노드입니다.

트리 관련 용어:

• Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
• Sibling (Brother Node): 동일한 Parent Node를 가진 노드
• Depth: 트리에서 Node가 가질 수 있는 최대 Level

트리의 주요 종류:

1. 이진 트리(Binary Tree): 각 노드가 최대 두 개의 자식 노드를 갖는 트리입니다.
   • 이진 탐색 트리(Binary Search Tree, BST): 각 노드의 왼쪽 서브트리에는 해당 노드보다 작은 값의 노드들이, 오른쪽 서브트리에는 해당 노드보다 큰 값의 노드들이 위치하는 이진 트리입니다.
   • AVL 트리: 균형 이진 탐색 트리로, 모든 노드에서 왼쪽과 오른쪽 서브트리의 높이 차이가 최대 1인 이진 탐색 트리입니다.
   • 레드-블랙 트리: 균형 이진 탐색 트리의 한 종류로, 각 노드에 색깔을 부여해 트리의 높이를 균형있게 유지합니다.
2. B-트리(B-tree): 트리의 각 노드가 여러 개의 자식 노드를 갖을 수 있는 트리로, 특히 데이터베이스와 같은 대용량 저장 시스템에서 사용됩니다.
3. 트라이(Trie): 문자열을 저장하고 검색하는데 효율적인 트리 자료구조로, 각 노드가 문자를 저장하고 자식 노드들은 해당 문자를 기반으로 구성된 문자열의 나머지 부분을 저장합니다.

트리 자료구조는 파일 시스템, 데이터베이스, 라우팅 알고리즘 등 다양한 분야에서 사용되며, 탐색, 삽입, 삭제 등의 연산을 효율적으로 수행할 수 있습니다.