Hash Table

CHOYEAH·2023년 10월 31일

해시테이블

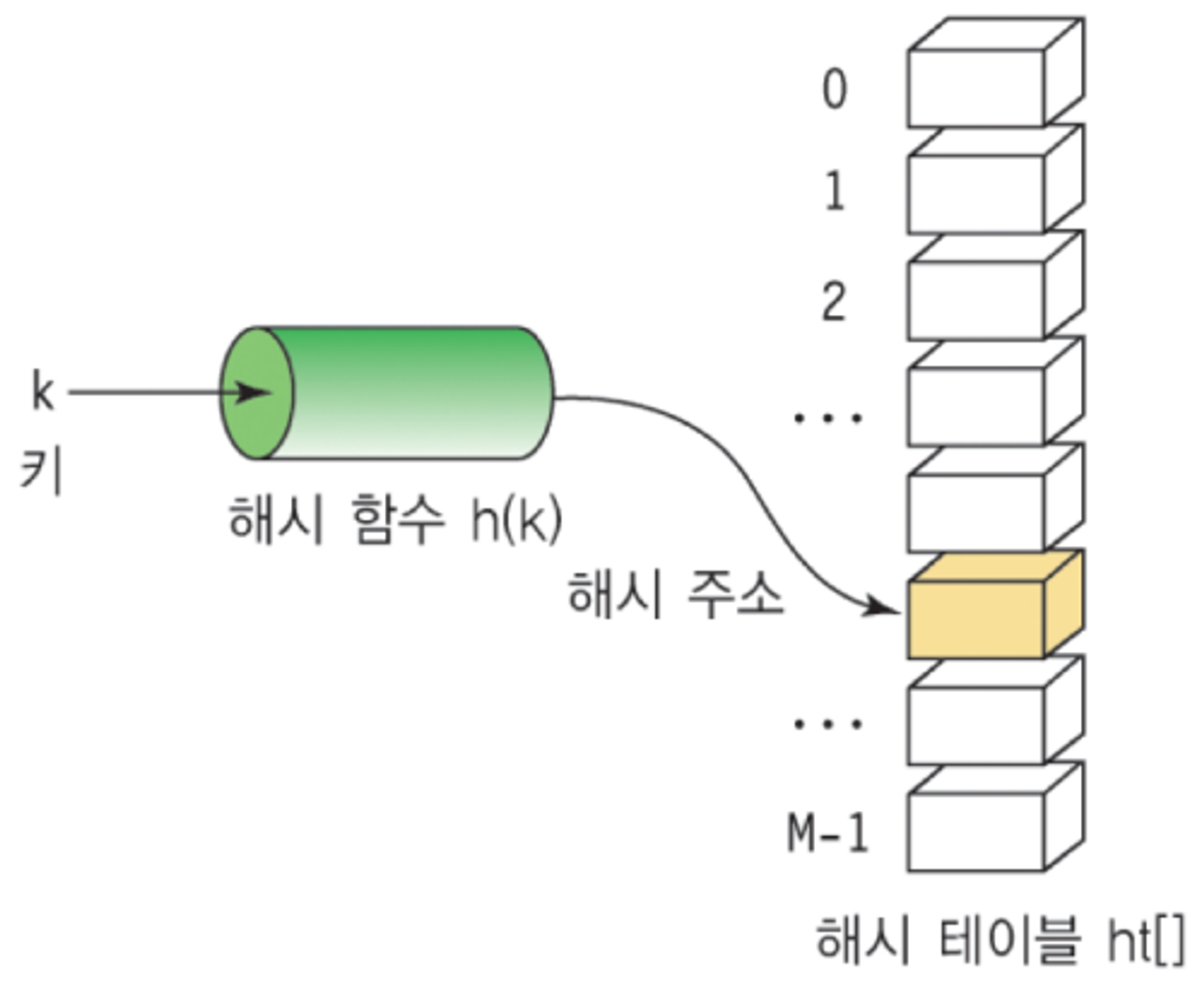
해시 테이블(Hash Table)은 키(key)와 값(value)을 쌍으로 저장하는 자료구조입니다. 해시 테이블의 핵심은 키를 입력으로 받아서 해시 함수(Hash Function)를 통해 고유한 인덱스를 생성하고, 이 인덱스를 배열의 위치로 사용해 값을 저장하는 것입니다. 이로 인해 빠른 검색, 삽입 및 삭제를 가능하게 합니다.

해시 테이블을 이해하는 데 중요한 개념은 다음과 같습니다:

해시 함수(Hash Function): 해시 함수는 키를 받아서 고유한 숫자(해시 값)를 생성하는 함수입니다. 이 해시 값은 배열의 인덱스로 사용됩니다. 좋은 해시 함수는 입력 키를 균일하게 분포시켜 해시 충돌(두 개 이상의 키가 동일한 해시 값으로 계산되는 경우)을 최소화합니다.
해시 테이블의 크기: 해시 테이블은 배열을 기반으로 하므로, 크기가 고정되어 있습니다. 해시 테이블의 크기는 해시 함수가 생성할 수 있는 고유한 해시 값의 범위를 결정합니다. 해시 테이블의 크기가 작으면 해시 충돌이 더 자주 발생할 수 있으며, 크기가 크면 메모리 공간이 낭비될 수 있습니다.
충돌 해결(Collision Resolution): 해시 충돌이 발생하면 두 개 이상의 키가 동일한 인덱스에 저장되어야 합니다. 이 문제를 해결하기 위해 여러 가지 충돌 해결 방법이 존재합니다. 대표적인 방법으로는 개별 체이닝(Chaining)과 오픈 어드레싱(Open Addressing)이 있습니다.

개별 체이닝(Chaining): 각 인덱스 위치에 연결 리스트를 사용하여 충돌이 발생한 키-값 쌍을 저장합니다. 키-값 쌍이 추가될 때마다 연결 리스트에 노드를 추가하여 충돌을 해결합니다.
오픈 어드레싱(Open Addressing): 충돌이 발생할 경우, 다른 인덱스를 찾아서 키-값 쌍을 저장하는 방식입니다. 선형 탐사(Linear Probing), 이차 탐사(Quadratic Probing) 및 더블 해싱(Double Hashing)과 같은 방법을 사용하여 충돌이 발생한 경우 다음 저장 위치를 찾을 수 있습니다.

사용 예

해시 테이블은 빠른 검색, 삽입 및 삭제를 제공하므로, 데이터베이스, 캐싱, 심볼 테이블, 맵 등과 같은 다양한 애플리케이션에서 사용됩니다. 다음은 해시 테이블의 몇 가지 일반적인 사용 사례입니다:

데이터베이스: 해시 테이블은 데이터베이스에서 인덱싱을 구현하는 데 사용됩니다. 키를 기반으로 빠르게 레코드를 찾을 수 있게 해줍니다.
캐싱: 캐시는 컴퓨터 시스템에서 자주 사용되는 데이터의 복사본을 저장하는 공간입니다. 해시 테이블은 캐시에서 데이터를 빠르게 검색하고 저장하는 데 사용됩니다.
심볼 테이블: 프로그래밍 언어에서 심볼 테이블은 변수나 함수 이름과 그에 대응하는 메모리 주소를 저장합니다. 해시 테이블을 사용하여 심볼 테이블을 구현하면 컴파일러나 인터프리터가 심볼을 빠르게 찾을 수 있습니다.
해시 세트(Hash Set): 중복을 허용하지 않는 키의 집합을 만드는 데 해시 테이블을 사용할 수 있습니다. 값은 저장하지 않고 키만 사용하여 빠른 검색 및 삽입을 가능하게 합니다.
해시 맵(Hash Map): 키-값 쌍을 저장하는 자료구조로, 해시 테이블을 기반으로 구현됩니다. 해시 맵은 키를 기반으로 빠르게 값을 검색하거나 저장할 수 있습니다.

해시 테이블의 단점은 충돌 해결 메커니즘이 추가적인 오버헤드를 발생시킬 수 있다는 것입니다. 또한, 해시 테이블의 크기가 고정되어 있어 메모리를 효율적으로 사용하기 어렵습니다. 그러나 충돌을 최소화하고, 적절한 크기를 선택하면 해시 테이블은 매우 빠른 검색, 삽입 및 삭제를 제공하는 효율적인 자료구조로 작동합니다.

1. 해쉬 구조

Hash Table: 키(Key)에 데이터(Value)를 저장하는 데이터 구조
Key를 통해 바로 데이터를 받아올 수 있으므로, 속도가 획기적으로 빨라짐
파이썬 딕셔너리(Dictionary) 타입이 해쉬 테이블의 예: Key를 가지고 바로 데이터(Value)를 꺼냄
보통 배열로 미리 Hash Table 사이즈만큼 생성 후에 사용 (공간과 탐색 시간을 맞바꾸는 기법)
파이썬에서는 해쉬를 별도 구현할 이유가 없음 - 딕셔너리 타입 사용하면 됨

2. 알아둘 용어

해쉬(Hash): 임의의 값을 고정 길이로 변환하는 것
해쉬 테이블(Hash Table): 키 값의 연산에 의해 직접 접근이 가능한 데이터 구조
해싱 함수(Hashing Function): Key에 대해 산술 연산을 이용해 데이터 위치를 찾을 수 있는 함수
해쉬 값(Hash Value) 또는 해쉬 주소(Hash Address): Key를 해싱 함수로 연산해서, 해쉬 값을 알아내고, 이를 기반으로 해쉬 테이블에서 해당 Key에 대한 데이터 위치를 일관성있게 찾을 수 있음
슬롯(Slot): 한 개의 데이터를 저장할 수 있는 공간

"버킷"은 각 해시 값에 대응하는 배열을 의미하고, "슬롯"은 배열 내의 개별 위치를 나타냅니다.

결론적으로, 이 두 용어는 서로 바꿔 사용되기도 하며, 일부 참고자료에서는 약간의 의미 차이가 있을 수 있습니다. 이를 이해하고 문맥에 따라 적절한 용어를 사용하는 것이 중요합니다.

저장할 데이터에 대해 Key를 추출할 수 있는 별도 함수도 존재할 수 있음

3. 해쉬 테이블 - 장점 / 단점 / 적합,부적합한 상황 / 주의사항

장점:

빠른 검색, 삽입, 삭제 속도: 해시 테이블은 평균 O(1) 시간 복잡도로 데이터를 검색, 삽입 및 삭제할 수 있습니다. 이는 효율적인 검색 속도를 요구하는 상황에서 큰 이점입니다.
키-값 쌍 저장: 해시 테이블은 키-값 쌍을 저장하므로, 키를 통해 값에 쉽게 액세스할 수 있습니다.

단점:

충돌: 여러 키가 동일한 해시 값에 매핑될 때 충돌이 발생합니다. 충돌 해결을 위한 추가 메커니즘이 필요하며, 이로 인해 성능이 저하될 수 있습니다.
메모리 사용량: 해시 테이블은 고정된 크기를 가지며, 일부 공간이 사용되지 않을 수 있습니다. 이로 인해 메모리 사용량이 비효율적일 수 있습니다.
해시 함수의 중요성: 좋은 해시 함수를 선택하는 것이 중요합니다. 그렇지 않으면, 해시 테이블의 성능이 저하되며, 충돌이 빈번하게 발생할 수 있습니다.

적합한 상황:

빠른 검색이 필요한 경우: 키-값 쌍을 기반으로 빠른 검색이 필요한 경우 해시 테이블을 사용할 수 있습니다.
중복 데이터를 효율적으로 처리해야 하는 경우: 해시 세트를 사용하여 중복 데이터를 처리할 수 있습니다.
키-값 쌍 저장이 필요한 경우: 키를 통해 값을 검색하거나 저장해야 하는 경우 해시 테이블이 적합합니다.

부적합한 상황:

데이터 정렬이 필요한 경우: 해시 테이블은 데이터를 정렬된 순서로 저장하지 않습니다. 정렬된 데이터 구조가 필요한 경우, 해시 테이블보다 이진 검색 트리와 같은 다른 자료구조를 사용하는 것이 좋습니다.
공간 효율성이 중요한 경우: 공간 효율성이 중요한 경우, 해시 테이블보다는 메모리 사용량이 더 적은 다른 자료구조를 사용하는 것이 좋습니다.

주의사항:

해시 함수 선택: 좋은 해시 함수는 데이터를 균일하게 분포시켜 해시 테이블의 성능을 최적화합니다. 성능 저하와 충돌을 최소화하기 위해 적절한 해시 함수를 선택하는 것이 중요합니다.
충돌 해결 전략: 충돌이 발생할 때 해시 테이블 성능에 영향을 미치는 충돌 해결 전략을 고려해야 합니다. 일반적인 충돌 해결 전략은 체이닝(연결 리스트 사용)과 개방 주소법(선형 조사, 이차 조사, 더블 해싱)입니다. 상황에 따라 적절한 충돌 해결 전략을 선택해야 합니다.
해시 테이블 크기 및 확장: 해시 테이블의 초기 크기와 확장을 결정하는 것이 중요합니다. 해시 테이블이 너무 작으면 충돌이 빈번하게 발생하고, 너무 크면 메모리 낭비가 발생할 수 있습니다. 일반적으로 로드 팩터(load factor)를 사용하여 해시 테이블 크기와 확장을 결정합니다. 로드 팩터가 임계값을 초과하면 해시 테이블을 확장해야 합니다.
보안: 해시 테이블은 해시 함수에 의존하기 때문에, 악의적인 사용자가 해시 충돌을 악용하여 시스템 성능을 저하시킬 수 있습니다. 이를 방지하기 위해 암호학적 해시 함수를 사용하거나, 해시 테이블을 무작위화하는 기술을 사용할 수 있습니다.
데이터 정렬: 해시 테이블은 데이터를 정렬된 순서로 저장하지 않습니다. 정렬된 순서로 데이터를 처리해야 하는 경우에는 다른 자료구조를 사용하는 것이 더 적합합니다.

이러한 사항들을 염두에 두고 해시 테이블을 사용하면, 효율적이고 안정적인 성능을 얻을 수 있습니다.

4. 해쉬 테이블 저장공간 안에서 충돌 문제를 해결하는 기법 두 가지

4-1. Chaining 기법

해쉬 테이블 저장공간 외의 공간을 활용하는 기법
링크드 리스트 자료 구조를 사용해서 데이터를 추가로 뒤에 연결시켜서 저장

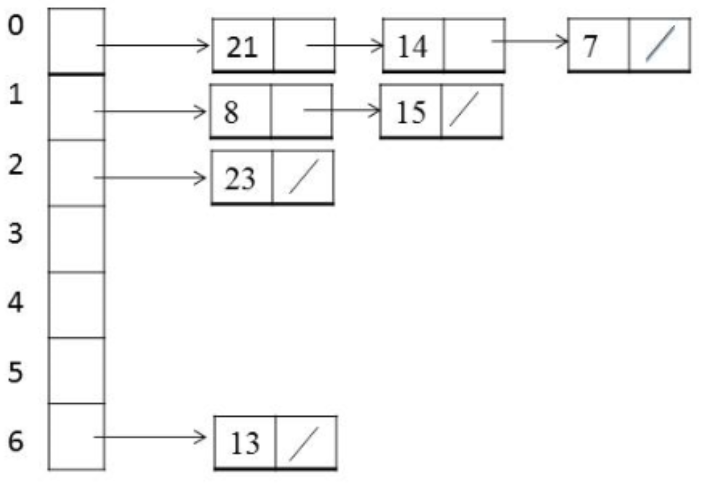
4-2. Linear Probing 기법

저장공간 활용도를 높이기 위한 기법
충돌이 일어나면 해당 hash address의 다음 address부터 맨 처음 나오는 빈 공간에 저장

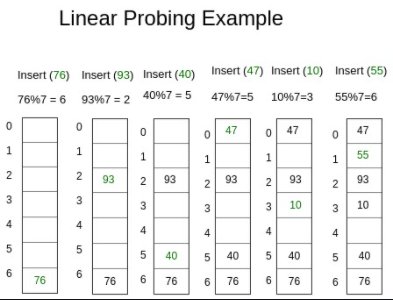
5. SHA-256

해쉬 테이블 구현에 사용될 SHA-256 미리보기

주어진 값에 고정된 길이(64)의 16진수를 리턴한다.
인자의 값이 조금이라도 틀리다면 다른 결과값을 리턴한다.
복호화가 불가하다.

import hashlib

data = 'test'.encode() # 스트링을 꼭 인코딩 시켜 사용한다.
hash_object = hashlib.sha256()
hash_object.update(data)
hex_dig = hash_object.hexdigest()
print (hex_dig) # 9f86d081884c7d659a2feaa0c55ad015a3bf4f1b2b0b822cd15d6c15b0f00a08

len('9f86d081884c7d659a2feaa0c55ad015a3bf4f1b2b0b822cd15d6c15b0f00a08')
# 64

print('test'.encode()) # 인코딩시 스트링 앞에 b가 붙는다.
# b'test'

6. Chaining 기법을 적용한 해쉬 테이블

Python

Chaining 기법을 적용한 해쉬 테이블

import hashlib

hash_table = list([0 for i in range(16)])

def get_key(data):
    hash_object = hashlib.sha256()
    hash_object.update(data.encode())
    hex_dig = hash_object.hexdigest()
    return int(hex_dig, 16)

def hash_function(key):
    return key % 16

def save_data(data, value):
    index_key = get_key(data)
    hash_address = hash_function(index_key)
    if hash_table[hash_address] != 0:
        for index in range(len(hash_table[hash_address])):
            if hash_table[hash_address][index][0] == index_key:
                hash_table[hash_address][index][1] = value
                return
        hash_table[hash_address].append([index_key, value])
    else:
        hash_table[hash_address] = [[index_key, value]]
    
def read_data(data):
    index_key = get_key(data)
    hash_address = hash_function(index_key)

    if hash_table[hash_address] != 0:
        for index in range(len(hash_table[hash_address])):
            if hash_table[hash_address][index][0] == index_key:
                return hash_table[hash_address][index][1]
        return None
    else:
        return None

print (hash('Dave') % 8)
print (hash('Dd') % 8)
print (hash('Dg') % 8)
print (hash('Df') % 8)
print (hash('Di') % 8)
# 5
# 2
# 3
# 5
# 2

save_data('Di', '8880008880')
save_data('Dd', '1201023010')
save_data('Data', '3301023010')
read_data('Dd')
# '1201023010'

hash_table
# [0,
#  0,
#  [[599905164450819986, '1201023010'], [2979456850781706866, '8880008880']],
#  0,
#  0,
#  [[-6126081656233692051, '8880008880']],
#  [[-794735671643054914, '3301023010']],
#  0]

Linear Probing 기법을 적용한 해쉬 테이블

import hashlib

hash_table = list([0 for i in range(16)])

def get_key(data):
    hash_object = hashlib.sha256()
    hash_object.update(data.encode())
    hex_dig = hash_object.hexdigest()
    return int(hex_dig, 16)

def hash_function(key):
    return key % 16

def save_data(data, value):
    index_key = get_key(data)
    hash_address = hash_function(index_key)
    if hash_table[hash_address] != 0:
        for index in range(hash_address, len(hash_table)):
            if hash_table[index] == 0:
                hash_table[index] = [index_key, value]
                return
            elif hash_table[index][0] == index_key:
                hash_table[index][1] = value
                return
    else:
        hash_table[hash_address] = [index_key, value]

def read_data(data):
    index_key = get_key(data)
    hash_address = hash_function(index_key)
    
    if hash_table[hash_address] != 0:
        for index in range(hash_address, len(hash_table)):
            if hash_table[index] == 0:
                return None
            elif hash_table[index][0] == index_key:
                return hash_table[index][1]
    else:
        return None

print (hash('dd') % 8)
print (hash('dg') % 8)

# save_data('dd', '7777777777')
# save_data('dg', '8888888888')
# read_data('dd')
# read_data('dg')
# '8888888888'

hash_table
# [0,
#  0,
#  0,
#  0,
#  0,
#  0,
#  0,
#  [1434459913659973535, '7777777777'],
#  [-4344317883337336537, '8888888888'],
#  0]

JS

Chaining 기법 적용

    class LinkedListNode {
      constructor(key, value, next = null) {
        this.key = key;
        this.value = value;
        this.next = next;
      }
    }
    
    class HashTable {
      constructor(size = 50) {
        this.size = size;
        this.buckets = new Array(size).fill(null);
      }
    
      hash(key) {
        let hashValue = 0;
        for (const char of key) {
          hashValue += char.charCodeAt(0);
        }
    
        return hashValue % this.size;
      }
    
      set(key, value) {
        const index = this.hash(key);
    
        if (!this.buckets[index]) {
          this.buckets[index] = new LinkedListNode(key, value);
    			return;
        } 
    
        let currentNode = this.buckets[index];
        while (currentNode !== null) {
          // When met same key
          if (currentNode.key === key) {
            currentNode.value = value;
            return;
          }
          if (currentNode.next === null) {
            currentNode.next = new LinkedListNode(key, value);
            return;
          }
          currentNode = currentNode.next;
        }
        
      }
    
      get(key) {
        const index = this.hash(key);
        let currentNode = this.buckets[index];
        while (currentNode !== null) {
          if (currentNode.key === key) {
            return currentNode.value;
          }
          currentNode = currentNode.next;
        }
    
        return undefined;
      }
    
      delete(key) {
        const index = this.hash(key);
    
        if (this.buckets[index] === null) {
          return;
        }
    
        if (currentNode.key === key) {
          this.buckets[index] = currentNode.next;
          return;
        }
    
        let previousNode = currentNode;
        let currentNode = currentNode.next;
        while (currentNode !== null) {
          if (currentNode.key === key) {
            previousNode.next = currentNode.next;
            return;
          }
    
          previousNode = currentNode;
          currentNode = currentNode.next;
        }
    
        return;
      }
    }
    
    // Test cases
    const testHashTable = new HashTable();
    
    testHashTable.set("apple", "delicious");
    testHashTable.set("banana", "tasty");
    testHashTable.set("orange", "sweet");
    
    console.log(testHashTable.get("apple")); // 출력: "delicious"
    console.log(testHashTable.get("banana")); // 출력: "tasty"
    console.log(testHashTable.get("orange")); // 출력: "sweet"
    console.log(testHashTable.get("grape")); // 출력: undefined
    
    testHashTable.set("banana", "very tasty");
    console.log(testHashTable.get("banana")); // 출력: "very tasty"
    
    testHashTable.delete("orange");
    console.log(testHashTable.get("orange")); // 출력: undefined
    
    testHashTable.set("watermelon", "juicy");
    console.log(testHashTable.get("watermelon")); // 출력: "juicy"
    
    testHashTable.delete("apple");
    console.log(testHashTable.get("apple")); // 출력: undefined

위 구현된 해시 테이블에서는 연결 리스트를 사용하여 충돌을 처리하고 있습니다. 이러한 구조에서 버킷은 해시 테이블의 각 인덱스를 나타내며, 슬롯은 연결 리스트의 각 노드를 의미합니다.
예를 들어, 아래와 같은 데이터를 저장한다고 가정해 보겠습니다.

    hashTable.set("firstName", "John");
    hashTable.set("lastName", "Doe");
    hashTable.set("age", 30);
    hashTable.set("city", "New York");

추상적으로 표현하면, 해시 테이블의 구조는 다음과 같이 됩니다.

    buckets: [
      null,
      { key: "firstName", value: "John", next: { key: "city", value: "New York", next: null } },
      null,
      { key: "lastName", value: "Doe", next: null },
      null,
      { key: "age", value: 30, next: null },
      ...
    ]

이 구조에서는:

"buckets"는 해시 테이블의 배열을 나타냅니다.
각 인덱스는 "버킷"이라고 부릅니다. 버킷은 해시 함수의 결과에 따라 키-값 쌍이 저장되는 위치입니다.
각 버킷에는 연결 리스트의 첫 번째 노드가 저장되어 있습니다. 연결 리스트의 각 노드를 "슬롯"이라고 부릅니다. 슬롯은 해당 버킷에 저장된 키-값 쌍을 포함합니다.
연결 리스트의 노드는 "next" 프로퍼티를 사용하여 다음 노드와 연결됩니다. 충돌이 발생한 경우, 새로운 슬롯이 연결 리스트에 추가되어 다음 노드를 가리키게 됩니다.

이 구조를 사용하면, 같은 버킷에 여러 개의 슬롯을 저장할 수 있으며, 충돌이 발생해도 연결 리스트를 통해 여러 키-값 쌍을 저장할 수 있습니다.

체이닝(Chaining) 방식을 사용할 상황:

충돌 발생 확률이 높을 때: 체이닝 방식은 연결 리스트를 사용하여 충돌이 발생한 경우에도 자료구조를 쉽게 확장할 수 있습니다.
데이터의 삽입, 삭제가 빈번한 경우: 체이닝 방식에서는 연결 리스트를 사용하기 때문에, 데이터의 삽입과 삭제가 간편하고 빠릅니다.
성능 요구사항이 높은 경우: 체이닝 방식은 충돌 처리가 비교적 빠르기 때문에 성능 요구사항이 높은 상황에서 적합합니다. 하지만, 메모리 사용량이 높아질 수 있으므로 이 점을 고려해야 합니다.

선형 탐사 방식의 해시 테이블

    class HashTable {
      constructor(size = 50) {
        this.size = size;
        this.buckets = new Array(size).fill(null);
      }
    
      hash(key) {
        let index = 0;
        for (let char of key) {
          index += char.charCodeAt(0);
        }
    
        return index % this.size;
      }
    
      isCollision(index, key) {
        return this.buckets[index] !== null && this.buckets[index].key !== key;
      }
    
      set(key, value) {
        let index = this.hash(key);
        while (this.isCollision(index, key)) {
          index = (index + 1) % this.size;
        }
        this.buckets[index] = { key, value };
      }
    
      get(key) {
        let index = this.hash(key);
    
        while (this.buckets[index] !== null) {
          if (this.buckets[index].key === key) {
            return this.buckets[index].value;
          }
    
          index = (index + 1) % this.size;
        }
        return undefined;
      }
    
      delete(key) {
        let index = this.hash(key);
    
        while (this.buckets[index] !== null) {
          if (this.buckets[index].key === key) {
            this.buckets[index] = null;
          }
          index = (index + 1) % this.size;
        }
      }
    }
    
    // Test cases
    const hashTable = new HashTable();
    hashTable.set("firstName", "John");
    hashTable.set("lastName", "Doe");
    hashTable.set("email", "john.doe@example.com");
    hashTable.set("age", 30);
    
    console.log(hashTable.get("firstName")); // 출력: "John"
    console.log(hashTable.get("lastName")); // 출력: "Doe"
    console.log(hashTable.get("email")); // 출력: "john.doe@example.com"
    console.log(hashTable.get("age")); // 출력: 30
    
    hashTable.set("lastName", "Smith");
    console.log(hashTable.get("lastName")); // 출력: "Smith"
    
    hashTable.delete("lastName");
    console.log(hashTable.get("lastName")); // 출력: undefined
    
    // 충돌 테스트
    hashTable.set("collision1", "value1");
    hashTable.set("collision2", "value2");
    hashTable.set("collision3", "value3");
    
    console.log(hashTable.get("collision1")); // 출력: "value1"
    console.log(hashTable.get("collision2")); // 출력: "value2"
    console.log(hashTable.get("collision3")); // 출력: "value3"
    
    hashTable.delete("collision2");
    console.log(hashTable.get("collision1")); // 출력: "value1"
    console.log(hashTable.get("collision2")); // 출력: undefined
    console.log(hashTable.get("collision3")); // 출력: "value3"

선형 탐사(Linear Probing) 방식과 체이닝(Chaining) 방식은 해시 테이블에서 충돌을 처리하는 방법입니다. 어떤 방식을 사용할지 결정하는 데는 여러 요인이 있지만, 주요한 기준은 충돌의 발생 확률, 메모리 사용량 및 성능에 관한 요구사항입니다.

선형 탐사(Linear Probing) 방식을 사용할 상황:

충돌 발생 확률이 낮을 때: 충돌이 적게 발생하면 선형 탐사 방식은 빠르게 빈 슬롯을 찾을 수 있습니다.
메모리 사용량을 최소화하려는 경우: 체이닝 방식은 연결 리스트를 사용하기 때문에 추가적인 메모리가 필요하게 됩니다. 선형 탐사 방식은 해시 테이블 내에서 충돌을 처리하기 때문에 추가적인 메모리 사용량이 적습니다.
데이터의 삽입, 삭제가 빈번하지 않은 경우: 선형 탐사 방식에서는 삭제 시 충돌 처리가 복잡해질 수 있습니다. 따라서 삽입과 삭제가 비교적 적은 경우에 선형 탐사 방식을 고려할 수 있습니다.

7. 시간 복잡도

일반적인 경우(Collision이 없는 경우)는 O(1)
최악의 경우(Collision이 모두 발생하는 경우)는 O(n)

해쉬 테이블의 경우, 일반적인 경우를 기대하고 만들기 때문에, 시간 복잡도는 O(1) 이라고 말할 수 있음

검색에서 배열과 해쉬 테이블의 시간 복잡도 비교

16개의 배열에 데이터를 저장하고, 검색할 때는 O(n)
16개의 데이터 저장공간을 가진 해쉬 테이블에 데이터를 저장하고, 검색할 때 O(1)

CHOYEAH

Move fast & break things

이전 포스트

Linked List

다음 포스트