[알고리즘 고득점 kit/프로그래머스/lv.3] 순위(플로이드 와샬)

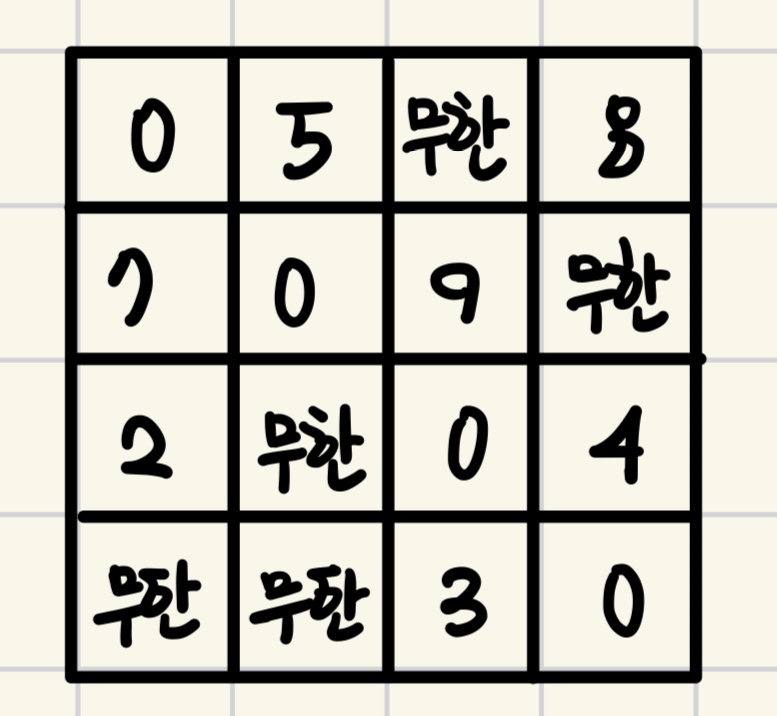
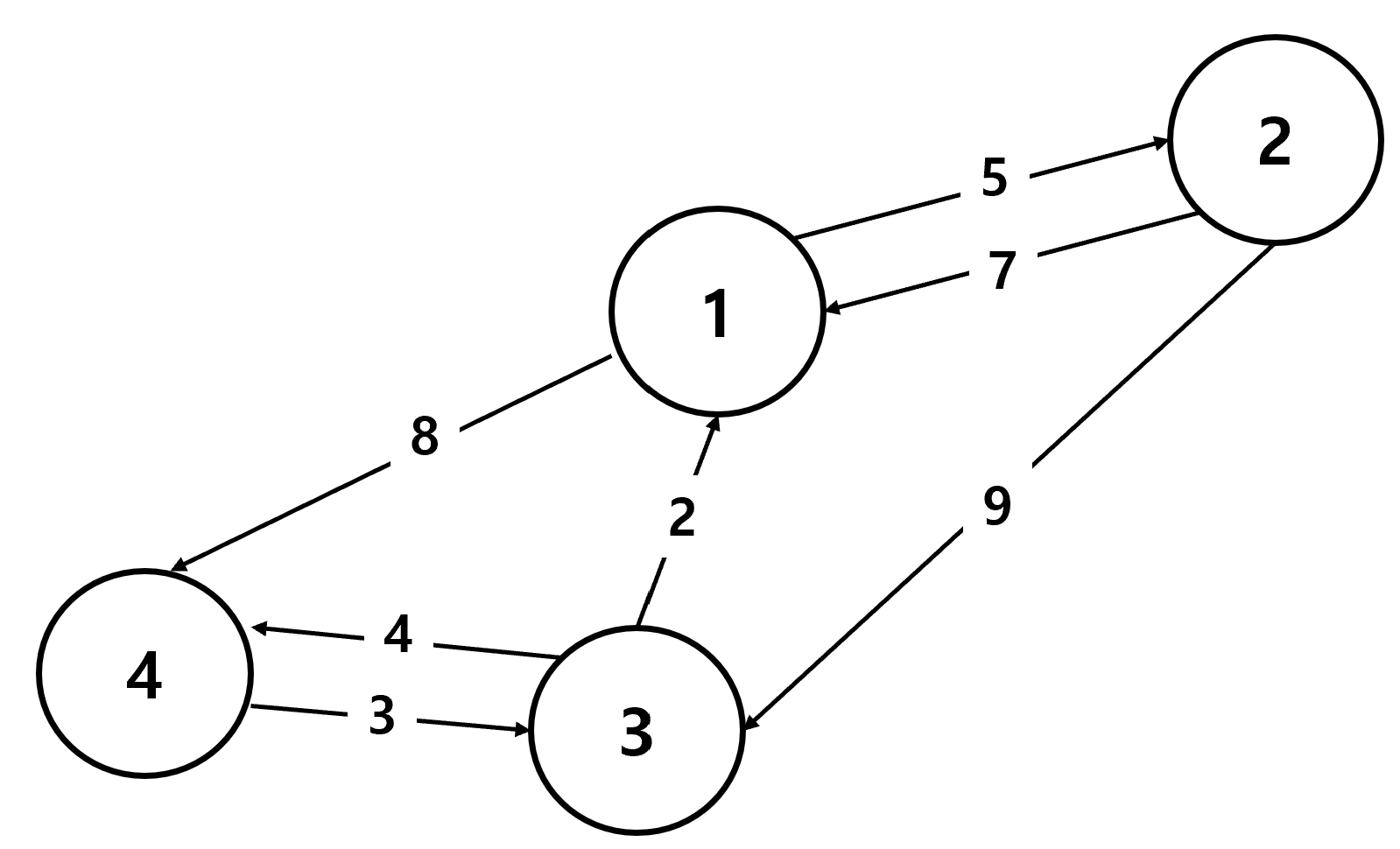
플로이드 와샬(Floyd-Warshall) 알고리즘이란?

한 정점에서 다른 정점으로의 최단 경로를 구할 때는 다익스트라 알고리즘을 사용할 수 있었다.
플로이드 와샬이란, 여러 정점에서 다른 정점으로의 최단 경로를 계산할 때 사용하는 알고리즘이었다.

다익스트라 알고리즘을 정리해보자면, 매 루프마다 각 시점마다 가장 최소 비용을 업로드해주는 방식이었다.
그에 반해, 플로이드 와샬은 '거쳐가는 정점' 을 기준으로 업로드해준다는 점에서 그 차이점을 보인다.

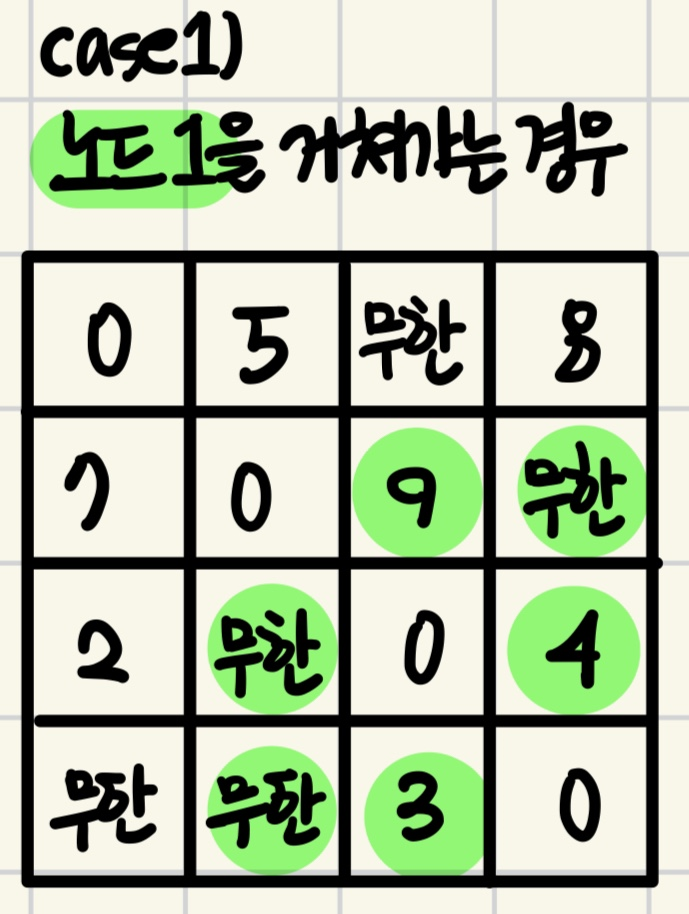
노드 1을 거쳐간다고 생각해보면,

X→Y로 가는 최소 비용 vs X에서 노드 1로 가는 비용 + 노드 1에서 Y로 가는 비용

다음 초록색인 부분에 대해서 업로드해준다고 생각하면 된다.

🖥️ 정답 코드

#include <string>
#include <vector>
#include <algorithm>
using namespace std;

// [A, B] --> A가 항상 B를 이김
int solution(int n, vector<vector<int>> results) {
    vector<vector<bool>> graph(n+1, vector<bool>(n+1, false));
    int answer = 0;
    for(int i = 0; i < results.size(); i++){
        graph[results[i][0]][results[i][1]] = true;
    }
    
    for(int k = 1; k <= n; k++){ // 거쳐가는 노드
        for(int i = 1; i <= n; i++){
            for(int j = 1; j <= n; j++){
                if(graph[i][k] && graph[k][j]) graph[i][j] = true;
            }
        }
    }
    for(int i = 1; i <= n; i++){
        int cnt = 0;
        for(int j = 1; j <= n; j++){
            if(graph[i][j]) cnt++;
            if(graph[j][i]) cnt++;
        }
        if(cnt == n-1) answer++;
    }
    return answer;
}