[프로그래머스 알고리즘 고득점 kit] [lv.3] 가장 먼 노드(그래프, bfs)

문제 설명

---

n개의 노드가 있는 그래프가 있습니다. 각 노드는 1부터 n까지 번호가 적혀있습니다. 1번 노드에서 가장 멀리 떨어진 노드의 갯수를 구하려고 합니다. 가장 멀리 떨어진 노드란 최단경로로 이동했을 때 간선의 개수가 가장 많은 노드들을 의미합니다.

노드의 개수 n, 간선에 대한 정보가 담긴 2차원 배열 vertex가 매개변수로 주어질 때, 1번 노드로부터 가장 멀리 떨어진 노드가 몇 개인지를 return 하도록 solution 함수를 작성해주세요.

제한사항

노드의 개수 n은 2 이상 20,000 이하입니다.
간선은 양방향이며 총 1개 이상 50,000개 이하의 간선이 있습니다.
vertex 배열 각 행 [a, b]는 a번 노드와 b번 노드 사이에 간선이 있다는 의미입니다.

입출력 예

---

n	vertex	return
6	[[3, 6], [4, 3], [3, 2], [1, 3], [1, 2], [2, 4], [5, 2]]	3

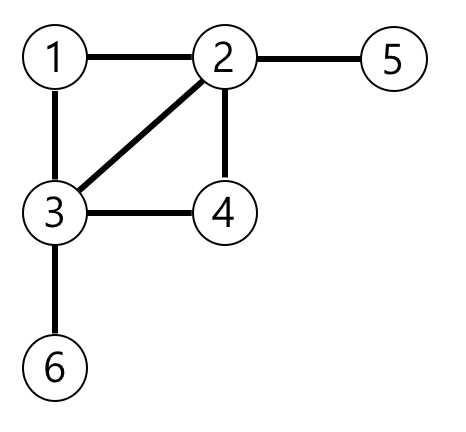
입출력 예 설명

예제의 그래프를 표현하면 아래 그림과 같고, 1번 노드에서 가장 멀리 떨어진 노드는 4,5,6번 노드입니다.

💡내가 생각한 아이디어

---

문제를 통해 이해해보기

---

lv.3 이지만, 그래프에 대한 기본 개념과 동시에 그래프를 탐색할 때는 dfs/bfs 등의 알고리즘을 이해한다고 알고 있으면 쉽게 풀리는 문제였다. 나는 bfs를 이용해서 처리했다.
(왜냐하면 거리 업데이트에 bfs+거리 배열 조합이 유리하기 때문.)
그리고 가중치가 다 1이라서

dist[nxt] = dist[cur] +1

이런 식으로 노드의 거리를 업데이트해주면 된다.

---

🖥️ 정답 코드

---

#include <string>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;

int solution(int n, vector<vector<int>> edge) {
    int answer = 0;
    vector<vector<int>> adj(n+1, vector<int>(0));
    for(int i = 0; i < edge.size(); i++){
        adj[edge[i][0]].push_back(edge[i][1]);
        adj[edge[i][1]].push_back(edge[i][0]);
    }
    queue<int> q;
    vector<int> dist(n+1, -1); // 각 노드마다 방문 거리 업데이트해줄 벡터 선언
    dist[1] = 0; // 방문 
    q.push(1);
    while(!q.empty()){
        int cur = q.front();
        for(int nxt: adj[cur]){
            if(dist[nxt]==-1) {
                dist[nxt] = dist[cur] + 1; // weight만큼 증가
                q.push(nxt);
            }
        }
        q.pop();
    }
    int maxDist = *max_element(dist.begin(), dist.end());
    for(int i = 0; i < dist.size(); i++){
        if(maxDist == dist[i]) answer++;
    }
    return answer;
}