Attention is all you need

chchch·2021년 11월 14일

DL NLP transformer

NLP

목록 보기

2/2

이번 포스팅은 transformer 모형의 핵심이 되는 attention 방법에 집중해서 다룬다.

Attention 방법

Seq2Seq 모형

기존의 기계번역에서 사용되던 Seq2Seq 모형은 인코더와 디코더 구조로 이루어져있다.

Seq2Seq 모형의 구조, 그림 출처

인코더(Encoder): 시간의 순서를 가지는 입력데이터를 순차적으로 받아 LSTM과 같은 RNN cell을 통해 적절한 feature learning을 거친 후 디코더로 전달
디코더(Decoder): 인코더로부터 전달받은 feature를 인코더와 비슷하게 RNN cell을 통해 순차적으로 결과를 반환

여기서 문제는 인코더를 통해 생성된 feature는 모든 시점이 압축된 길이가 1인 벡터라는 점이다. 예를들어, 위의 그림처럼 $n$ 시점마다 $p$ 차원의 입력값이 인코더로 들어온다면 총 입력데이터의 크기른 $n \times p$ 차원의 행렬로 생각할 수 있다. 하지만 인코더를 통해 디코더로 넘어가는 feature는 $1 \times d_m$ 차원의 벡터이다. 모델의 임베딩 차원( $d_m$ )을 아무리 키운다고 하더라도 손실이 생길 수 밖에 없다.

이와 같은 문제점을 해결하고자 attention 방법을 고안했다.

Attention

Attention 방법의 핵심은 모든 입력 시점의 정보를 사용해서 중요한 시점에 집중(attention)하자는 것이다. 번역이라는 특수한 task를 고려했기 때문에 이와 같은 아이디어가 발생했다는 생각이 든다(번역에서 단어와 번역 단어는 거의 일대일로 대응될테니).

그림 출처: 딥러닝을 이용한 자연어 처리 입문 위키독스

그렇다면 중요한 시점에 어떤식으로 집중을 할 수 있을까? 현재 번역해야하는 시점의 벡터와 모든 입력 단어의 벡터들과 유사도(벡터간 내적)를 구해 그 비율만큼 입력 단어 벡터를 조합한다. 여기서 그 유사도를 attention score라고 한다.

디코더의 $t$ 시점을 기준으로 인코더 시점과의 attention score 계산

$q_t$ : 디코더 $t$ 시점의 LSTM cell의 hidden state 벡터
$k_i, i\in\{1, \dots, T\}$ : 인코더 $i$ 시점의 LSTM cell의 hidden state 벡터
$q_t^\top k_i$ : 디코더의 $t$ 시점과 인코더의 $i$ 시점의 attention score(스칼라)
$s_t = [q_t^\top k_1 ~ \dots ~ q_t^\top k_T]^\top$ : 디코더의 $t$ 시점과 인코더 모든 시점의 attention score 벡터
$w_t = \text{softmax}(s_t) \in \mathbb{R}^T$ : 디코더의 $t$ 시점과 인코더 모든 시점의 attention weight 벡터 $\rightarrow$ 집중 비율
$w_t^\top \mathbf{1} = 1$

어탠션 비율은 어탠션 스코어를 softmax층을 통해 합이 1이 되도록 변환된 값이다.

위에서 계산한 비율을 가지고 디코더의 $t$ 시점을 기준으로 인코더 시점과의 attention value를 만든다.

디코더의 $t$ 시점을 기준으로 인코더 시점과의 attention value 계산

$K = [k_1, \dots, k_T]^\top \in \mathbb{R}^{T \times d_m}$ : 인코더 hidden state들을 쌓은 행렬
$c_t^\top = w_t^\top K \in \mathbb{R}^{1 \times d_m}$ : attention weight 벡터를 가중치로 한 hiddens state들의 가중 평균, attention value 벡터
$\rightarrow$ Attention value는 디코더의 $t$ 시점과의 연관성을 기반으로 입력정보를 사용하여 새롭게 생성한 피쳐

이후 $c_t$ 와 $k_t$ 를 결합한 벡터를 가지고 기존의 LSTM과 동일한 과정 수행을 수행한다.

Attention 방법은 입력과 출력 시점간의 연관성을 고려한 피쳐 학습 방법(feature learning method)

Transformer에서 attention

Transformer 모형의 RNN 기반의 모델의 순차적인 연산의 비효율성을 비판하고 병렬처리가 가능한 연산을 제시했다. 때문에 과감하게 입력 시점을 모아서 연산을 했으며 FFN(feed forward network) 구조를 사용하였다. Transformer 모형도 인코더와 디코더가 결합된 구조를 가지고 있다. 인코더와 디코더의 입력단에서 각각 self-attention이 수행되고 그 결과가 만나는 곳에서는 일반적인 입력-출력간의 attention 연산이 수행된다.

Transformer에서 attention이 이루어지는 위치와 종류, 그림 출처: UOS Optim lab 발표자료

Self-attention

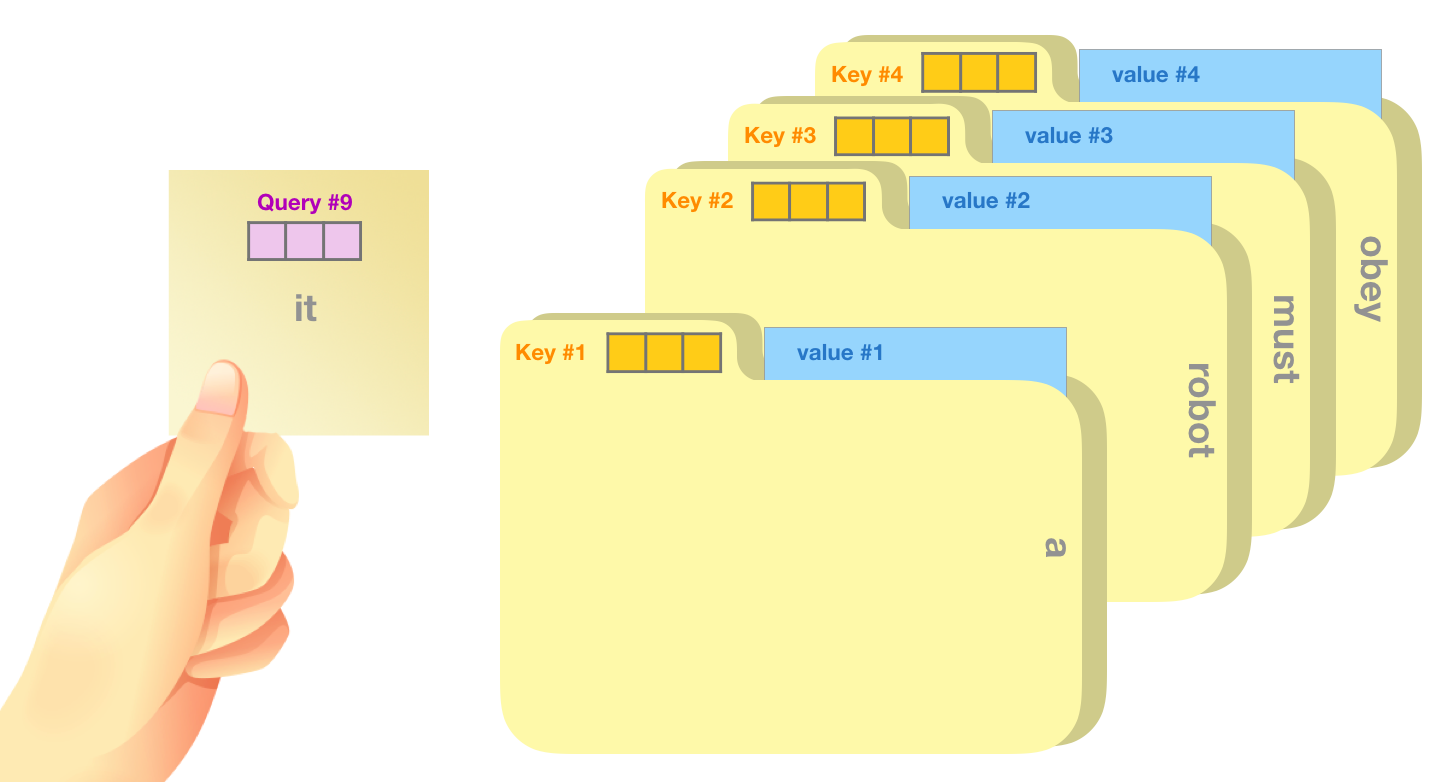
위에서 $t$ 시점을 기준으로 한다는 것과 각 연산의 결과가 벡터와 행렬을 특별히 언급한 이유가 있다. 바로 위에서 말했듯이 transformer에서 진행되는 attention들은 모든 시점을 동시에 진행하는 행렬끼리의 연산이다. 그리고 위에서 연산의 결과를 $q, k$ 를 사용한 이유도 비교를 쉽게 하기 위함이다. Query, Key, Value는 database에서 나온 용어로 query가 주어졌을시 key와 비교해서 value를 가져오는 과정과 유사해서 사용했다.

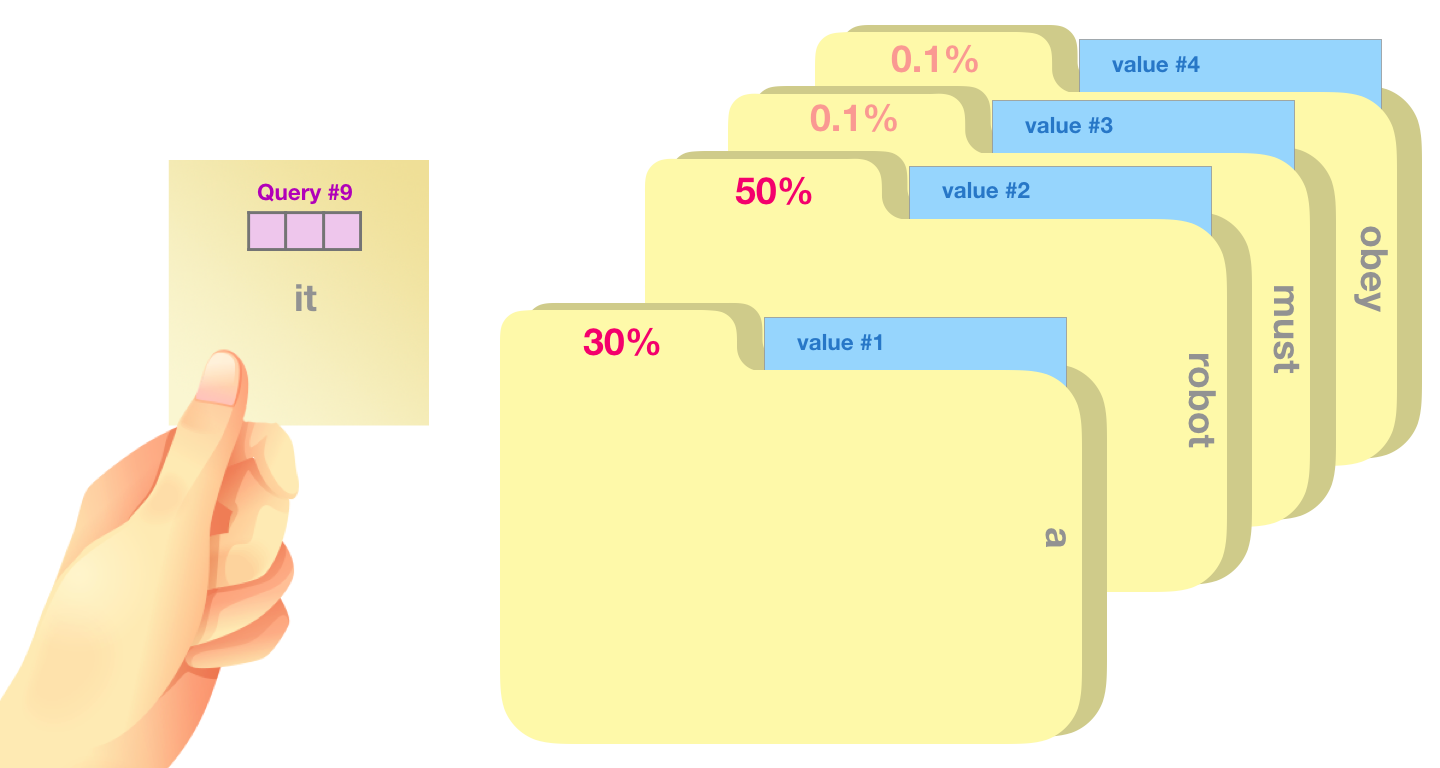Database에서 query, key, value와 attention의 작동 방식의 유사성, 그림 출처: Jay Alammar 블로그

먼저, transformer 모형에서는 입력간의 관계를 고려한 feature learning을 위해 self-attention이라는 방법을 고안했다. 그 연산은 다음과 같다. Self-attention을 하기 위해서는 하나의 임베딩 행렬( $X$ , 여기서는 입력 데이터 행렬)에 각각 다른 FFN을 거쳐 query $(Q)$ , key $(K)$ , value $(V)$ 를 생성

$Q = X W_{Q}$ 행렬
$K = X W_{K}$ 행렬
$V = X W_{V}$ 행렬
$Q$ 와 $K$ 를 가지고 attention score를 계산하고 attention weight를 계산
$V$ 의 attention weight만큼의 가중 평균으로 새롭게 피쳐 생성

Seq2Seq의 attention와 transformer의 Self-attention의 차이점은 다음과 같다.

Seq2Seq에서는 디코더 $t$ 시점의 attention 연산을 위해서는 $t-1$ 시점까지 attention 연산이 선행되어야함
$\rightarrow$ 디코더의 모든 시점에서 동시에 진행될 수 없어서 $t$ 시점 hidden state(벡터)에서만 계산함
Transformer는 순차적인 연산이 없어서 모든 시점에 대해서 동시에 attention을 진행할 수 있음
$\rightarrow$ $t$ 시점의 벡터만이 아닌 모든 시점 $(1, \dots, T)$ 의 행렬을 가지고 계산

Query

Attention: 디코더의 $t$ 시점의 hidden state(벡터)
Self-attention: 모든 시점의 단어 행렬 $X$ 와 $W_Q$ 의 곱(행렬)

Attention: 인코더의 모든 시점의 hidden state를 모은 행렬(행렬)
Self-attention: 모든 시점의 단어 행렬 $X$ 와 $W_K$ 의 곱(행렬)

Value

Attention: 인코더의 모든 시점의 hidden state를 모은 행렬(행렬)
Self-attention: 모든 시점의 단어 행렬 $X$ 와 $W_V$ 의 곱(행렬)

Self-attention 연산 과정

$\text{Attention}(Q, K, V) = \underbrace{\text{softmax}(\underbrace{\frac{Q K^\top}{\sqrt{d_m}}}_{\text{attention score}})}_{\text{attention weight}}V$
여기서 $d_m$ 은 행렬곱의 연산값이 너무 커지는 것을 방지하기 위한 조정 상수

$Q K^\top/\sqrt{d_m} \in \mathbb{R}^{T \times T} = [s_1, \dots, s_T]^\top$ : 모든 시점간의 attention score를 담은 행렬
$W = \text{softmax}(Q K^\top/\sqrt{d_m}) = [w_1, \dots, w_T]^\top \in \mathbb{R}^{T \times T}$
Attention $(Q, K, V)$ 의 첫번째 행:
$c_1 = \sum_{t=1}^{T} w_{1,t} v_t, \qquad \sum_{t=1}^T w_{1,t} = 1$

Self-attention의 의미
: 내부 단어들간의 연관성(문맥)을 고려한 피쳐 생성
예시) Hong likes a dog. He also likes a cat
"He" 단어의 문맥적인 의미를 주변의 단어들을 통해 새롭게 생성

입력 - 출력간의 attention

Transformer에서도 seq2seq와 동일하게 입력-출력간의 attention이 이루어지며 이는 self-attention과 $Q$ , $K$ , $V$ 를 이루는 행렬만 다르며 연산과정은 크게 다르지 않다. Masking이라는 방법을 통해 미리 정답을 알지 못하도록 하는 과정이 추가되지만 여기서는 생략하겠다.

$Q$ , 디코더에서 넘어온 행렬을 $W_{Q'}$ 와 곱해서 만든 행렬
$K$ , 인코더에서 넘어온 행렬을 $W_{K'}$ 와 곱해서 만든 행렬
$V$ , 인코더에서 넘어온 행렬을 $W_{V'}$ 와 곱해서 만든 행렬

아래의 계산된 attention weight 행렬를 통해 attention의 의도를 시각적으로 이해할 수 있다.

스페인어-영어 번역 작업에서 입력-출력 attention weight 행렬, 그림 출처: 그림 출처: Tensorflow 튜토리얼

Weight 행렬에서 입력되는 스페인어와 출력되야할 영어의 단어가 연결되었다. 노란색에 가까울수록 큰 weight를 가지는 값으로 스페인어 primeiro는 영어 first와 대응되었다.

입력-출력간의 attention은 Seq2Seq에서 attention과 동일하다. 번역 단어들과 입력 단어들간의 유사도를 계산하여 잘 대응되도록 하는 것이다.

Multihead attention

처음에 transformer는 연산의 효율성을 위해 병렬화가 이루어지도록 설계했다고 했다. 이는 multihead attention이라는 방법을 통해 수행되는데 attention 과정을 time-step이 아닌 feature 혹은 embedding dimension 방향으로 나누는 경우, 병렬화가 가능하다. $Q$ 와 $K^\top$ 의 곱을 아래의 그림처럼 동일한 크기로 나누어서 진행해도 서로 영향을 주지않는 것은 수식을 전개하면 알 수 있다.

Multihead attention 연산 원리, 그림 출처: UOS Optim lab 발표자료

마지막으로 attention 방법은 흡사 통계학에서 배우는 CCA(canonical correlation analysis)와 유사하다. CCA는 두 벡터의 correlation이 커지도록하는 선형변환을 구하는 방법이다. 특정한 조건하에서는 correlation이 거리(유사도)처럼 생각할 수 있으며 attention은 CCA의 제약조건 없이 수행되는 일반적인 방법으로 생각할 수 있다. Attention에 대한 포스팅은 여기서 마무리하며 연산과정이나 원리에 대한 시각적인 자료는 Jay Alammar 블로그에 많이 있으며 이해를 돕기에 매우 유용하다.

Attention(transformer) 후속연구

Attention 연산을 확장하여 발표된 흥미로운 연구 몇 가지를 소개하고 포스팅을 마무리하겠다.

On the Relationship between Self-Attention and Convolutional Layers: Self-attention이 convolution 연산을 포함하는 연산임을 밝히면서 transformer 기반의 모형이 비젼분야에서 성공 원인을 밝힌 연구
Set Transformer: 입력으로 집합을 받아 예측을 수행하는 transformer 모형
MQTransformer: 시계열 예측을 위한 transformer 모형

chchch

머신러닝과 통계학을 공부하는 사람

이전 포스트