석사과정 딥러닝 수업 막바지에 'Restricted Boltzmann Machines(RBM: 제한된 볼츠만 머신)'에 대해서 배울 기회가 있었다. 당시에 앞에서 배웠던 신경망 모형과 다르게 학습이 단순하지 않았던 RBM을 이해하기 어려웠다. 기존의 신경망 모형들은 결과적으로 역전파 알고리즘을 통해 미분값을 계산할 수 있으면 학습이 가능했다. 하지만 볼츠만 머신은 수식의 유도와 학습에 있어서 샘플링이 필요해서 쉽지 않았다.
이번에 RBM이 필요로 한 문제가 발생하여 다시 책을 폈다. 내용은 Goodfellow의 'Deep learning' 책과 전북대 오일석 교수님의 '기계 학습' 책을 참고했다. 그리고 수식의 전개와 표기법은 서울시립대 최호식 교수님의 교육 자료를 참고했다.
Restricted Boltzmann Machines(RBM)
볼츠만 머신은 이진 벡터(x∈{0,1}d)에 대한 확률 분포를 학습하기 위해 제안되었다. 학습된 확률분포를 통해서 새로운 데이터를 생성할 수 있다. 먼저, 확률분포를 모형화해야한다. 통계학에서는 가우시안 분포나 이진 변수이면 베르누이 분포 등을 통해 확률분포를 모형화했을 수 있지만 볼츠만 머신은 에너지 함수라는 물리학 개념을 사용했다.
Energy Function
볼츠만 머신에서는 확률분포를 다음의 에너지 함수를 통해서 정의한다.
p(x)=Zexp(−E(x)),
여기서 Z는 합이 1이 되기 위한 정규화항이고 E(x)가 벡터 x의 에너지를 나타내는 에너지 함수이다. 즉, x의 에너지(E(x))가 높을수록 x의 확률값은 낮아진다. 에너지 함수에 대한 개념이 물리 이론에서 나왔다고 하는데 현실에서는 에너지가 높은 상태의 상태는 드물고 에너지가 낮은 안전한 상태로 있기 때문이다. 통계학에서 말하는 "지수족 분포(exponential family)"와 흡사하다.
이제 에너지 함수(E)를 모형화해야한다. 볼츠만 머신에서는 에너지 함수 E를 모형화하는데 신경망 모형을 사용했다.
E(x,h)=−x⊤Rx−x⊤Wh−h⊤Sh−b⊤x−c⊤h
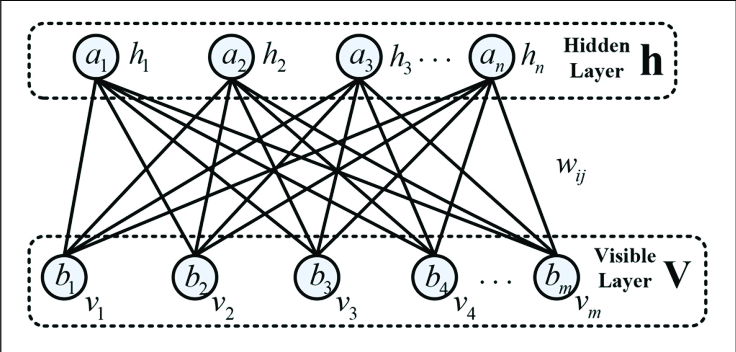
RBM은 x와 x, h와 h 사이의 관계는 고려하지 않는다. 그래서 모형에 제한을 두었기 때문에 제한된 볼츠만 머신이라고 한다. 제한을 두었지만 계산량을 훨씬 줄이니깐 모형의 편의성을 고려했다고 보는게 좋은 것 같다.
E(x,h)=−x⊤Wh−b⊤x−c⊤h
여기서는 데이터를 x로 표현을 했지만 다른 RBM 관련 문헌에서는 관측 가능하다(visible)고 해서 v로 표현했다.

위의 그림을 보면 두 에너지 함수의 차이를 쉽게 확인할 수 있을 것이다. 오른쪽의 RBM은 같은 층에 있는 노드들끼리의 연결선이 없다.
Derivative
학습을 위해서는 목적함수를 미분해서 목적함수를 최소화(혹은 최대화)하는 방향으로 모형의 파라미터(θ)들을 갱신한다. 따라서 위의 목적함수 즉, 에너지 함수를 미분해야한다.
pθ(x,h)pθ(x)=Zexp(−E(x,h)),=h∑Zexp(−E(x,h))=Zexp(−Fθ(x)),
여기서 ∑hexp(−E(x,h))=exp(−F(x))이고 Z=∑x~exp(−Fθ(x~))이다. 사실 RBM에서 Z를 계산하기가 매우 어렵다. 예를 들어 h가 100차원, x가 100차원이라고 하고 각각의 원소는 0 또는 1의 값을 가지므로 Z를 계산하기 위해서 2100×2100의 경우의 수에 대해서 합을 계산해야한다. 하지만 모형의 학습에 필요로 하는 것은 미분계수이다. 미분 수식을 예쁘게 전개하면 Z를 계산하지 않고도 미분 결과를 알 수 있다.
RBM의 목적함수는 에너지 함수를 사용해서 정의된 marginal likelihood pθ(x)를 최대화하는 것이다. 즉, 우리가 가지고 있는 데이터(x)의 likelihood를 높이는 것이다. log-likelihood, logpθ(x)를 모형의 파라미터(θ)에 대해서 미분해보자.
∂θ∂logpθ(x)=−∂θ∂Fθ(x)−∂θ∂logZ=−∂θ∂Fθ(x)+Z1×x~∑exp(−Fθ(x~))∂θ∂Fθ(x~)=−∂θ∂Fθ(x)+x~∑pθ(x~)∂θ∂Fθ(x~)
위에서 언급된 Z에 대한 식은 사라지고 뒤에 익숙한 항이 하나 생겼다. 바로 Fθ의 미분값의 기댓값이다.
여기서 log-likelihood를 n으로 나누더라도 최대화하는 방향은 똑같으므로 다음의 식을 사용하도록 한다.
∂θ∂logpθ(x)=n1i=1∑n∂θlogpθ(x(i))=−n1i=1∑n∂θ∂Fθ(x(i))+x~∑pθ(x~)∂θ∂Fθ(x~)
Fθ(x)는 h에 대한 marginal distribution이므로 hk∈{0,1}임을 이용하면 Fθ(x)는 다음과 같이 쓸 수 있다.
Fθ(x)=b⊤x−k=1∑qlog(1+exp(ck+Wkx)).
모형의 학습 파라미터에 대한 미분값은 다음과 같이 쓸 수 있다.
∂bj∂Fθ(x)∂ck∂Fθ(x)∂wjk∂Fθ(x)=−xj,=−1+exp(ck+Wkx)exp(ck+Wkx)=−p(hk=1∣x),=−xjp(hk=1∣x).
이제부터 학습 파라미터에 대한 편미분은 아래와 같이 log-likelihood를 n으로 나눈 것에 대한 편미분 값이다.
∂θj∂logpθ=n1i=1∑n∂θj∂logpθ(x(i))
이제 위의 편미분 값을 이용해 marginal distribution에 대한 편미분 계수를 구해보자.
∂bj∂logpθ(x)∂ck∂logpθ(x)∂wjk∂logpθ(x)=n1i=1∑nxj(i)−x~∑pθ(x~)x~j,=n1i=1∑np(hk(i)=1∣x(i))−x~∑pθ(x~)p(h~k=1∣x~),=n1i=1∑nxj(i)p(hk(i)=1∣x(i))−x~∑pθ(x~)x~jp(h~k=1∣x~).
위의 미분 결과를 보면 공통점이 있다. 3가지 결과 모두, 앞항은 데이터에 대한 경험적 분포(emperical distribution)에 의한 기댓값의 형태이고 뒷항은 모형에서의 확률(pθ)에 의한 기댓값의 형태이다.
여기에서 문제가 발생하는데 일반적인 딥러닝이나 머신러닝 모형에서는 우리가 갖고 있는 데이터(x(i))로 역전파를 이용해서 미분값을 계산할 수 있었다. 하지만, RBM에서는 미분결과의 뒷항 때문에 우리가 가진 데이터만으로 미분값을 계산하기가 불가능하다. 왜냐하면 뒷항은 pθ를 따르는 x~의 기댓값이기 때문이다.
더 자세하게 설명해보면, pemp를 현재 데이터(x(i)) 경험 분포(∑i=1nδx(i)/n)이라 하자. 우리가 갖고 있는 x(i)는 pemp를 따르고 그 기댓값은 n1∑i=1nf(x(i))의 형태로 계산되어진다. 뒷항은 x(i)을 가지고 계산하면 기댓값이라고 할 수 없다. 왜냐하면 x(i) ~ pemp이기 때문이다. 예로 베르누이 확률변수의 기댓값을 계산하는데 확률질량함수를 포아송 분포를 사용하면 안되는 것과 같은 이유이다.
그래서 x~를 pθ의 분포로 '샘플링' 해야한다.
Train: Contrastive Divergence Algorithm
갑자기 샘플링이 나와서 당황할 수 있다. 사실 머신러닝의 입문서에서 다루는 모형들은 대부분 샘플링을 필요로 하지 않는다. 말그대로 주어진 데이터에 기반해서 파라미터를 추정하면 그만이다. 하지만 입문을 벗어나 확률분포를 추론하는 모형과 같은 심화 모형들은 샘플링 과정을 거치게 된다. 예를 들면 "VAE"가 있다. VAE는 입문서에서 이론을 다루기에는 통계학적인 베이스가 상당히 요구되서 많이 어렵다. 아무튼 RBM을 학습하기 위해서는 위에 식에서 살펴보았지만 x~를 pθ의 분포로 샘플링해야한다.
RBM 학습을 위한 샘플링 방법으로는 'Gibbs sampling(깁스 샘플링)'을 사용한다. 깁스 샘플링은 MCMC(Markov Chain Monte Carlo) 방법 중 하나로 매우 간편하고 유용한 샘플링 방법이다. 깁스 샘플링은 쉽게 설명하면 샘플링 해야하는 대상이 m차원이라고 한다면, x~∈Rm 다음과 같이 샘플링을 한다.
x~j∼p(x~j∣x~1,…,x~j−1,x~j+1,…,x~m)
나머지 xi, i=j를 고정시키고 xj를 뽑는다.
RBM에서는 단순하다. 데이터 x를 통해 h를 계산한다. 그 다음 h를 통해 x~를 샘플링한다. 위의 깁스 샘플링의 식을 이용하면 다음과 같다.
x~j∼p(x~j∣h)
그리고 RBM에서는 조건부 확률을 아래의 식으로 계산한다.
p(hk(n)=1∣x(n))p(x~j(n)=1∣h(n))=sigmoid((Wx(n)+c)k)=sigmoid((W⊤h(n)+b)j)
위의 식은 이항변수라는 특징 덕분에 위와 같이 식이 쓰여지는 것을 확인할 수 있다. 확률을 계산했으면 0과 1을 가지는 이항변수를 생성하는 것은 균일분포(U(0,1))를 통해 쉽게 생성할 수 있다.
그런 다음 기댓값을 계산해서 파라미터를 업데이트한다. log-likelihood를 최대화하는 방향으로 업데이트를 해야하므로 아래의 식으로 업데이트한다.
bj(m+1)ck(m+1)wjk(m+1)=bj(m)+α(n1i=1∑nxj(i)−x~∑pθ(x~)x~j),=ck(m)+α(n1i=1∑np(hk(i)=1∣x(i))−x~∑pθ(x~)p(h~k=1∣x~)),=wjk(m)+α(n1i=1∑nxj(i)p(hk(i)=1∣x(i))−x~∑pθ(x~)x~jp(h~k=1∣x~)).
여기서 α는 학습률(learning rate)이다.
위와 같은 방법으로 학습하는 방법을 'Constrastive Divergence Algorithm'이라고 한다. 그리고 깁스 샘플링을 n 번 하면 'n-CD'라고 하는데 1-CD만 하더라도 충분하다는 것이 잘 알려져있다.
이번에 RBM에 대해서 공부해보았는데 RBM도 초창기 모형으로 지금은 많은 발전을 해왔다. 그 중 하나로 Wasserstein Distance를 이용한 RBM도 있다. 그리고 최근에는 RBM을 이용해 임베딩을 하는 기법도 많이 나오고 있으니 딥러닝을 공부하는 사람들에게는 좋은 공부거리가 될 것 같다.

안녕하세요, 우연히 들렀다가 댓글 남기려고 가입했습니다. RBM에 대한 자료를 찾기가 쉽지 않았는데 이렇게 정리해주셔서 감사합니다. 수식에 대한 설명이 큰 도움이 되었습니다.