선택 정렬
선택정렬
- 선택정렬이란, 배열 요소 중 최솟값을 찾아 첫번째 원소 값과 교환해주는 방식을, 하나의 원소만 남을 때까지 반복해주는 정렬 방식입니다.
정렬 방식
- 배열의 요소 중 최소값을 찾아준다.
- 이 최솟값과 배열의 첫번째 값을 바꿔준다.
- 맨 처음 위치를 뺀 나머지 리스트를 같은 방법으로 교체한다.
- 하나의 원소만 남을 때 까지 위의 1~3 과정을 반복하자.
GIF로 이해하는 선택 정렬의 동작 원리
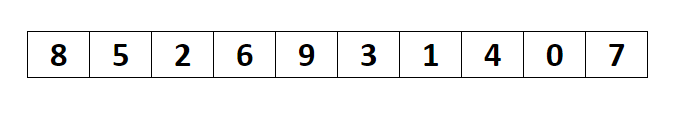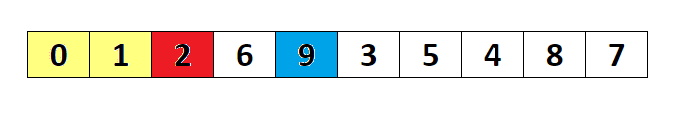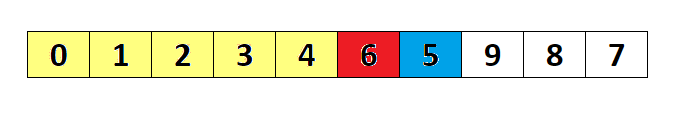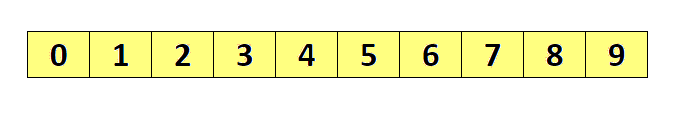
- 배열 요소에서 최솟값을 찾아준다.
- 최솟값이 위치한 인덱스 값으로 원래의 인덱스 값을 변경해준다.
- 최솟값이 위치한 곳과 비교를 시작한 위치의 값을 바꿔준다.
복잡도
시간 복잡도
- 첫 번째 회전에서의 비교 회수 : 1 ~ n-1 => (n-1)번
- 두 번째 회전에서의 비교 회수 : 2 ~ n-1 => (n-2)번- 이러한 원리를 계속적으로 반복하여 총 반복 횟수는
(n-1) + (n-2) + ... + 2 + 1 => n(n-1) / 2
공간 복잡도
- 주어진 배열 안에서 교환을 통해, 정렬이 수행되므로 O(n)이다.
장점
- 알고리즘이 단순하다.
- 정렬을 위한 비교 횟수는 많지만, 버블 정렬에 비해 실제로 값을 교환하는 횟수는 적다.
- 따라서, 많은 교환이 일어나야 하는 자료 상태에선 비교적 효율적이다. - 버블 정렬과 마찬가지로 정렬하고자 하는 배열에서 교환하는 방식
- 다른 메모리 공간을 필요로 하지 않는다 -> 제자리 정렬(in-place sorting)
단점
- 시간 복잡도가 O(n^2)으로 비효율적
- 불안정 정렬(Unstable Sort)이다.
구현 코드
package hw_0927;
public class SelectionSort {
public static int[] SelectionSort(int[] arr) {
int temp;
for (int i = 0; i < arr.length - 1; i++) {
int idx = i;
for (int j = i + 1; j < arr.length; j++) {
/*
* 바뀐 인덱스 값과 증가된 j값에 위치한 요소값과 계속적으로 비교,
* 즉, 배열의 최솟값을 찾아내서 최솟값의 인덱스를 idx에 할당
*/
if (arr[j] < arr[idx]) {
idx = j;
}
}
/*
* 찾아낸 인덱스 값을 활용하여, 인덱스에 위치한 값이랑 첫번째 값이랑 바꿔줌
*/
temp = arr[i];
arr[i] = arr[idx];
arr[idx] = temp;
}
return arr;
}
public static void printArr(int[] arr) {
for (int element : arr) {
System.out.print(element + " ");
}
System.out.println();
}
public static void main(String[] args) {
int arr[] = { 8, 2, 1, 5, 6, 9 };
System.out.println("-----정렬 전-----");
printArr(arr);
System.out.println("-----정렬 후-----");
SelectionSort(arr);
printArr(arr);
}
}출력 결과
나가면서
오늘은 선택 정렬의 원리와 복잡도를 알아보고 코드로 구현해보았습니다.
다양한 정렬 방식이 있는데, 얼른 다른 정렬 방식도 마스터 해야할 것 같습니다.
선택 정렬의 동작 원리는 배열의 최솟값을 찾아내는 방식이었던 것 같습니다. 이를 코드로 어떻게 표현할지 잘 고민했기 때문에, 비교적 수월하게 구현했었던 것 같습니다.