삽입 정렬
삽입 정렬
- 삽입 정렬은, 현재 비교하고자 하는 타겟(target)을 정하고, 타겟이 이전의 원소보다 더 작을 경우, 자리를 교환해주는 정렬 방식이다.
- 데이터를 비교하면서 찾기 때문에 비교 정렬
- 정렬의 대상이 되는 데이터 외에 추가적인 공간은 필요하지 않으므로 제자리 정렬(in-place sort) 이기도 하다.
- 거의 정렬된 배열에서 효율이 아주 좋다
- 버블 정렬이나, 선택 정렬 보다 평균 비교 횟수에 대한 기대값이 상대적으로 적기 때문에 평균 시간복잡도가 O(N^2)인 정렬 알고리즘 중에서는 빠른 편에 속한다.
GIF로 이해하는 삽입정렬
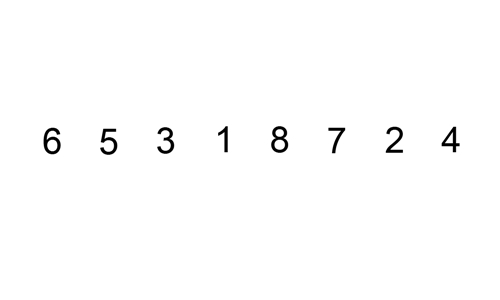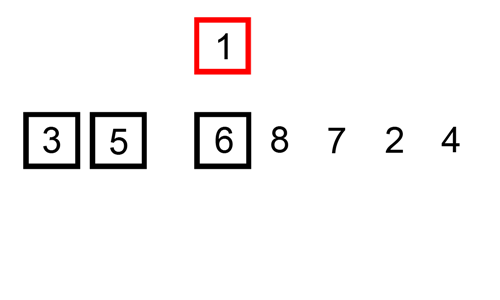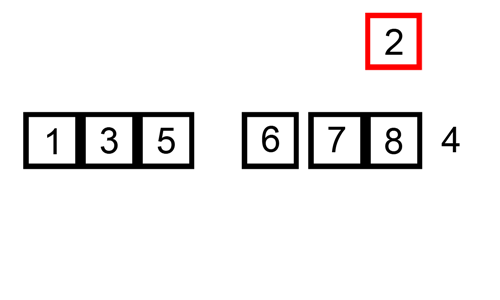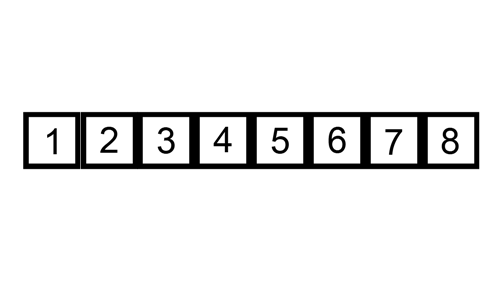
- target을 지정해준다. (첫번째 타겟은 두번째 원소)
- 타겟에 위치한 값과 타겟으로 부터 왼쪽에 위치한 값을 비교해준다.
- 타겟의 값이 왼쪽에 위치한 요소들보다 더 작은 경우, 큰 값들을 오른쪽으로 밀어준다.
3.1 이 때, 타겟의 값이 왼쪽의 위치한 요소보다 작지 않으면, 왼쪽은 이미 정렬이 되어 있다고 가정하므로 비교 작업을 멈추고 다음 타겟의 비교를 시작한다.- 타겟의 값을 변경된 인덱스에 배치해준다.
복잡도
시간복잡도
최선 : O(n)
- 최선의 경우, 타겟 숫자가 바로 왼쪽에 위치한 수와 비교하는 것이다. 이 때, 타겟의 수가 더 크면, 왼쪽은 이미 정렬이 되어 있다고 가정하기 때문에 시간 복잡도는 O(n)이 된다.
최악 : O(n^2)
- 최악의 경우에는, 타겟 숫자가 이전의 위치한 숫자들보다 더 작기 때문에 결국 n-1번 까지 비교해야할 것이다. 따라서 n(n-1)/2가 되므로, 시간 복잡도는 O(n^2)이 될 것이다.
평균 : O(n^2)
- 최선의 경우[O(n)]와 최악의 경우 [O(n^2)]를 합쳐서 나눈 결과가 평균일 것이다. 시간 복잡도는 상한선을 의미하기 때문에 아래와 같은 결과를 가질 수 있다.
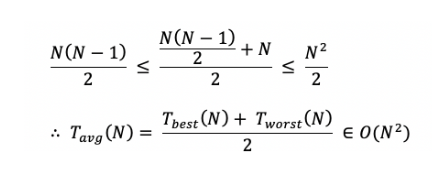
- 결과적으로, 최상의 경우와 최악의 경우의 평균으로 보더라도 '상한선'이라는 개념에 의해 O(n^2)이 정설로 본다.
구현 코드
package hw_0928;
public class InsertionSort {
public static int[] insertionSort(int [] arr) {
for(int i=1;i<arr.length;i++) {
int target = arr[i];
int j;
for(j = i-1 ; j>=0; j--) {
//타겟의 값이 자신의 왼쪽에 있는 값보다 작다면
if(target < arr[j]) {
arr[j+1] = arr[j]; // 배열의 요소를 하나 밀어줌
//왼쪽의 요소와 비교해서 , 더 크면 이미 정렬이 되어있다고 가정했기 때문에 반복문 탈출
}else {
break;
}
}
arr[j+1] = target;
}
return arr;
}
public static int[] insertionSort2(int []arr) {
for(int i=1;i<arr.length;i++) {
int target = arr[i];
int j = i-1;
while(j>=0 && arr[j] > target) {
arr[j+1] = arr[j];
j--;
}
arr[j+1] = target;
}
return arr;
}
public static void printArr(int []arr) {
for ( int element : arr) {
System.out.print(element + " ");
}
System.out.println();
}
public static void main(String[] args) {
int arr[] = { 12,2,1,6,8,3,52,45 };
System.out.println("-----정렬 전-----");
printArr(arr);
System.out.println("-----정렬 후-----");
insertionSort(arr);
printArr(arr);
}
}
실행 결과

나가면서
오늘은 삽입 정렬을 구현해 보았습니다.
이론적으로는 금방 이해 했지만, 타겟보다 큰 값들을 뒤로 밀어주는 것을 코드로 표현하는데 있어 조금 어렵게 생각했던 것 같습니다.
최선의 경우 또한 고려해주지 못했고, 레퍼런스를 보며 이해할 수 있었습니다.
이를 통해, 삽입 정렬이 O(n^2)의 평균 시간 복잡도를 가지는 다른 정렬 방법보다 기대 비교 횟수가 더 작아 어느 정도 정렬이 되어 있는 배열에서는 효율이 좋다는 것을 이해할 수 있었습니다.