Gravity-Inspired Graph Autoencoders for Directed Link Prediction

한줄요약
graph에서 directed한 link를 예측한다.
ABSTRACT
autoencoder(AE)와 variational_autoencoders(VAE)는 강력한 노드 임베딩 방법이고, graph에서 연결이 되어있어야하지만 연결이 안 되어 있는 노드도 연결해주는 링크 예측 문제를 성공적으로 활용되었다. 하지만 여기서 edge는 방향이 없는 undirected한 graph이기 때문에 실제 응용 프로그램에 제한적이다. 본 논문에서는 이를 확장하여 directed한 graph를 제안한다.
1. INTRODUCTION
AE/VAE를 활용하여 link를 예측하는 것은 간단히 말하면 저차원 벡터 공간으로 노드 벡터를 압축하여 저차원 공간에서의 거리가 비슷하면 link를 연결해주는 것이다. 앞에서도 말했지만 기존에 AE/VAE를 활용한 link 예측은 undirected한 graph이기 때문에 약간의 문제가 있다. SNS로 예를 들면 평범한 일반인은 연예인 아이유님에게 강하게 link 되겠지만 그 반대의 경우는 아닐 것이다. 이 논문의 저자는 이러한 undirected한 문제점을 지적하면서 directed한 것을 제안한다. 추천시스템에서는 밥 말리(레게 장르의 전설이라고 불림)가 신인 무명 레게 밴드의 가장 비슷한 아티스트로 추천될 수 있지만 그 반대의 경우는 아닐 것이다. 이런 예시들은 undirected한 graph에서는 해결할 수 없는 문제이다. 오직 directed한 graph에서만 할 수 있는 것들이다.
본 논문에서는 벡터 공간 노드 임베딩에서 비대칭 관계를 재구성할 수 있는 새로운 디코더를 도입한다. 여기서 새로운 디코더는 뉴턴의 만유인력 이론에서 영감을 받았다고 한다. 그리고 저자는 이것은 directed graph에 대한 첫 번째 연구라고 말한다.
2. PRELIMINARIES
V = n개의 nodes, E = m개의 edges, G = graph로 나타내고 G = (V, E)로 적는다.
여기서 G의 인접행렬은 A로 나타내고, 노드의 특징 벡터들을 X로 나타낸다.
A는 nxn 행렬이고, X는 nxf 행렬이다.(f는 각 노드의 특징 벡터의 크기)
인접행렬은 아래 사진과 같이 나타내어지는 것이고,
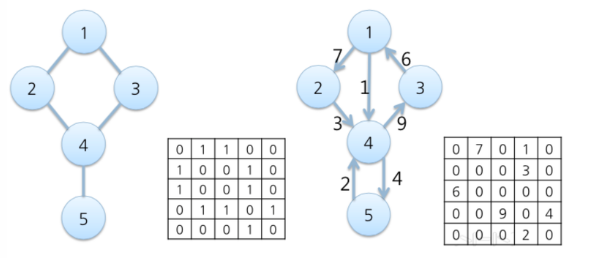
나는 graph는 자료구조/알고리즘에서 배우고 오랜만이라 X라는 특징벡터가 잘 이해가 안 됐는데, 아래 그림과 같은 느낌이라고 생각하면 된다. 각 노드마다 특징벡터가 있는 것이고(아래 그림에서는 f=3이다) 각 노드 n개를 합쳐서 행렬로 만들면 nxf 행렬 X가 되는 것이다.
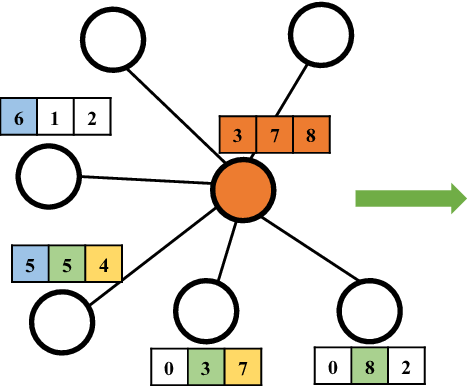
(참고로 이 논문을 이해하려면 GCN(Graph Convolution Network)은 알아야하는데, https://www.youtube.com/watch?v=YL1jGgcY78U 이 강의를 먼저 듣고 오면 좋을 것 같다. graph 기본 내용과 GCN까지 설명해준다.)
3. A GRAVITY-INSPIRED MODEL FOR DIRECTED GRAPH AE AND VAE
이제 앞에서 말했듯이 directed한 link 예측을 위한 모델을 제시한다. 저자는 'gravity'에서 영감을 얻었는데, 뉴턴의 만유인력 이론을 활용한다. 지구에서 달의 거리와 달에서 지구의 거리는 같지만 중력에 의한 달의 지구 방향 가속도는 지구가 달을 향해 가속하는 것보다 크다. 왜냐하면 지구가 달보다 더 무겁기 때문이다. 쉬운 예를 들자면 아이유님과 같은 영향력이 큰 아티스트와 신인 가수가 있을 때, 아이유의 mass가 더 크기 때문에 신인 가수에서 아이유로 가는 link는 강할 것이고, 그 반대의 경우는 아닐 것이다. 그래서 음원 스트리밍 사이트에서 추천을 해줄 때 아이유와 같은 영향력이 큰 아티스트는 끌어당기는 힘이 강하기 때문에 무명의 아티스트의 노래를 듣다가 아이유가 추천될 가능성은 매우 높고, 그 반대의 경우는 아닐 것이다. 이런 예시들이 directed가 있어야하는 이유이다.
중력 F를 구하는 공식은 다음과 같고, 1->2로 가는 것과 2->1로 가는 공식도 함께 첨부한다.
다시 말하지만 mass가 작은 것이 큰 것으로 가는 link는 강해야하고, 그 반대의 경우는 약해야한다. 아까 예시를 들어 말하면 신인가수가 아이유에게 가는 link는 강해야하고, 그 반대의 경우는 매우 약해야한다. 신인가수와 아이유는 너무 차이가 크기 때문에 아이유 -> 신인가수로 가는 link는 0으로 없을 수도 있다.(논문 Figure 1에서 사진으로 보여주는데, mass가 큰 node들은 바깥으로 나가는 링크보다는 안으로 들어오는 링크가 훨씬 많다.)
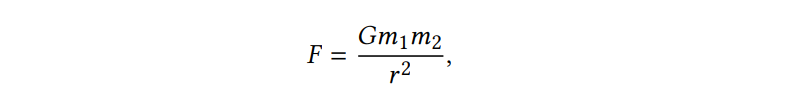
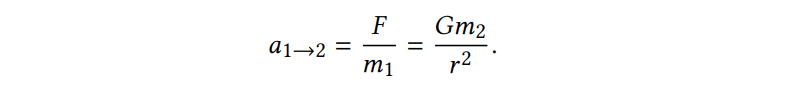
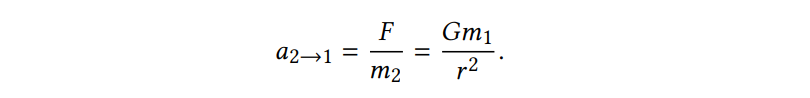
일반화 하면 node-i에서 node-j로 가는 공식은 다음과 같고, 압축된 임베딩 공간 Z에서 거리를 구해 r을 구할 수 있다.
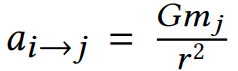
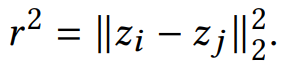
여기 논문에서는 큰 값을 제한하고, weight가 없는 edge일 때(Aij가 0 or 1) 시그모이드 함수를 사용하여 log를 씌워주면 편리하다는 이유로 log를 씌워준다.
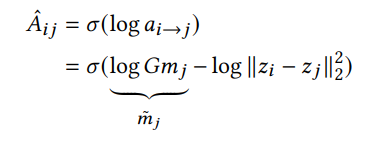
Gravity-Inspired Directed Graph AE
AutoEncoder(AE)에는 압축하는 encoder와 재구성하는 decoder가 있다.
encoder -> 인접행렬 A와 특징벡터 X를 GCN(Graph Convolution Network)에 넣고 d+1차원으로 압축한다. d차원은 노드의 잠재적 표현이고, 1차원은 mass의 추정치이다. M 위에 "~" 표시는 log를 씌웠다는 것을 의미한다. log를 씌우나 안 씌우나 학습에는 동일하지만 log를 씌우면 계산이 편해진다.
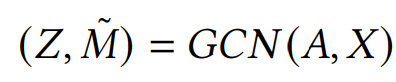
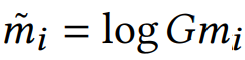
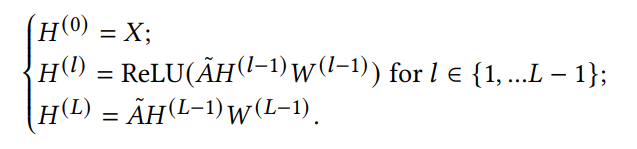
decoder -> 여기서는 인접행렬 A를 재구성하면 된다. 이때 활용되는 것은 (1)mass와 (2)압축된 Z 공간에서 node-i와 node-j의 거리이다.
아래 식을 보면 node-i에서 node-j로 가는 link의 weight를 예측하는 것인데,
(1) 아까 말했던 것처럼 node-j의 mass가 크다면 node-i는 j에 강하게 끌려와야 한다. 그래서 node-j의 mass가 크면 클수록 예측 link의 weight는 커진다.
(2) 그리고 압축된 Z 공간에서의 거리가 작으면 작을수록 가까이 있다는 뜻이기 때문에 작을수록 link의 weight는 커진다.
마지막으로 시그모이드 함수를 씌워서 값이 0~1 사이에 들어가게 하면 아래와 같은 식이 나오고, gradient descent로 cross entropy loss를 줄이면서 재구성 loss를 최소화하게 훈련한다.
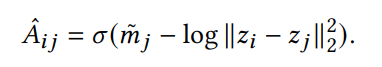
Gravity-Inspired Directed Graph VAE
encoder -> VAE는 mu와 sigma 이렇게 2개로 압축이 되어서 Z에 샘플링 되기 때문에 GCN이 아래와 같이 2개가 필요하다.
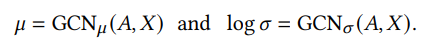
decoder -> 앞에 AE decoder와 재구성 식은 동일하기 때문에 다시 설명하지는 않겠다. gradient descent로 ELBO를 최대화하도록 훈련한다는 점만 다르다.
Generalization of the Decoder
AE/VAE의 디코더는 아래와 같다. 이것은 사실 앞에 1이 곱해진 것이 생락된 것이다. 다시 말해 (1)mass와 (2)거리가 1:1의 비율로 계산된다는 것이다.
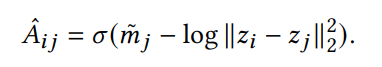
하지만 (1)mass와 (2)거리에서 거리를 더 중요하게 보고 더 가중치를 두고 싶다면 앞에 람다를 곱하면 된다. 그렇게 되면 식에서 거리가 차지하는 비중이 더 높아질 것이다. 식은 아래와 같다.
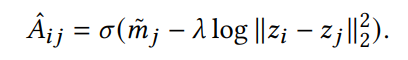
4. EXPERIMENTAL ANALYSIS
Task 1 : General Link Prediction
Task 2 : Biased Negative Samples (BNS.) Link Prediction
Task 3 : Bidirectionality Prediction
이렇게 3가지 task로 실험을 하고 AUC와 AP로 평가를 한다. 결과는 아래와 같다.
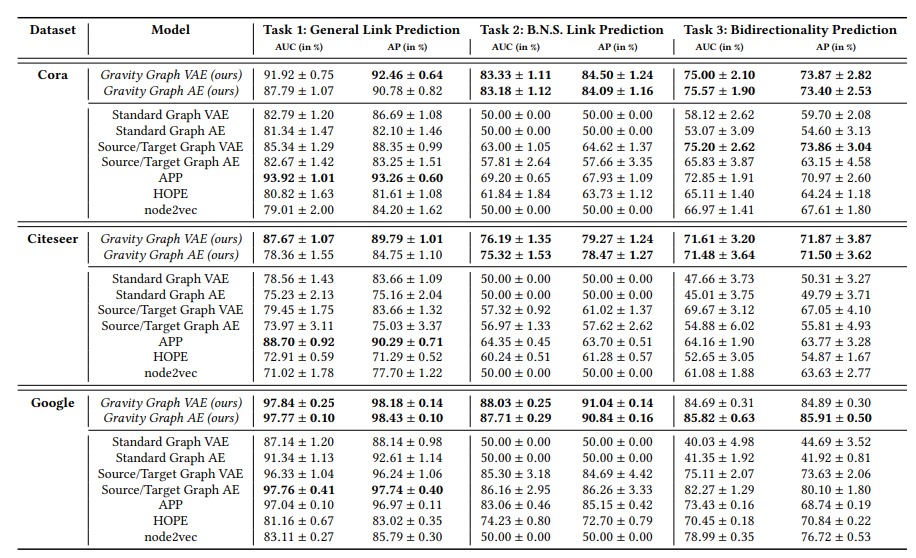
추가로 아까 람다에 대하여 설명했었는데 그에 대한 실험 결과도 첨부한다.
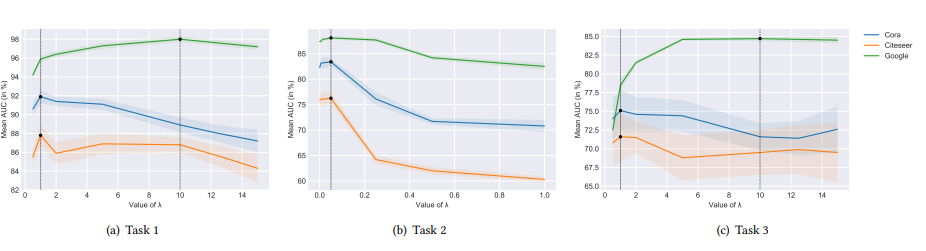
5. CONCLUSION
graph AE/VAE를 사용하여 directed한 graph에서 노드 임베딩 표현을 학습하는 뉴턴 중력에 영감을 받아 새로운 방법을 제시한 것이 이 논문이다.
code
official code가 아래 링크에 올라와있습니다.
https://github.com/deezer/gravity_graph_autoencoders