RNN~Transformer

YONG·2024년 6월 24일

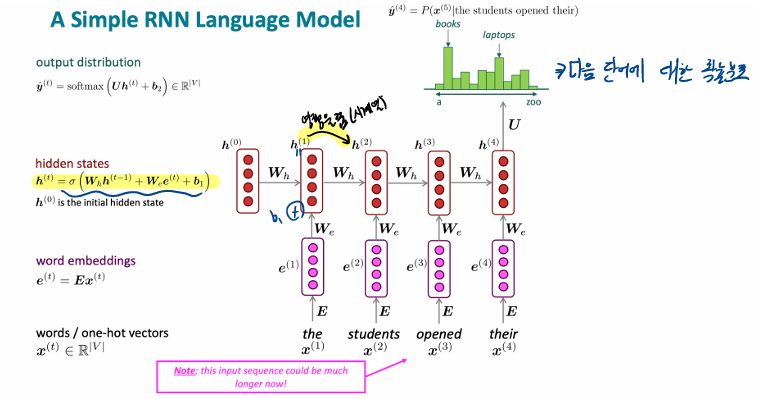
언어 모델

: 다음 단어가 무엇이 올지 맞추는 것이 목표!!

the students opened their __

언어모델에 사용되는 신경망들

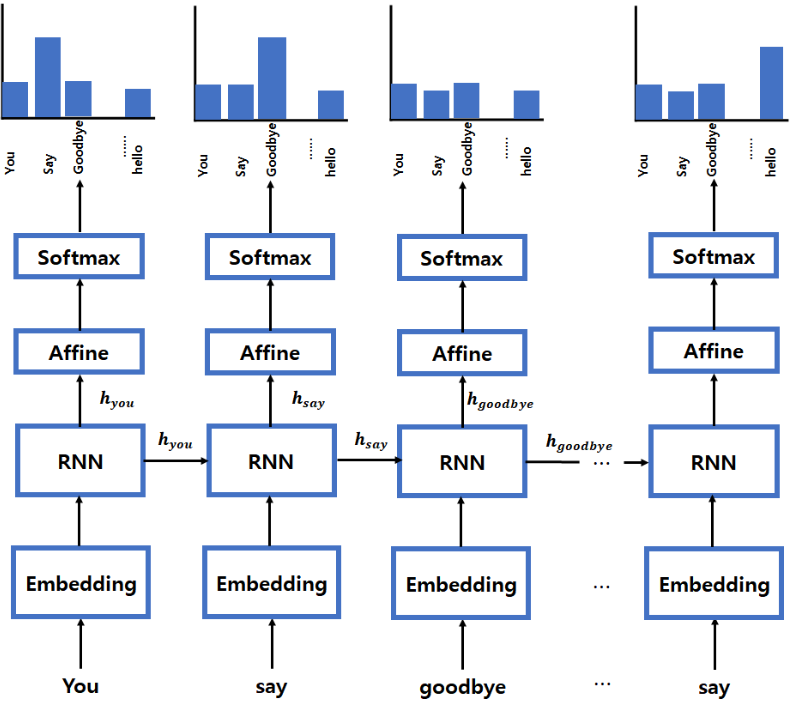
1.RNN

  • RNN 손실함수 계산 법
  1. 큰 코퍼스를 얻는다. 일단 일련의 단어들 x1, x2, ..., xT로 구성되어 있다.
  2. RNN의 입력값으로 준다. 그리고 매 단계 t마다 결과 분포를 계산한다.
  3. 각 스텝 t마다의 예상되는 확률 분포 y^(t)\hat{y}(t)와 진짜 다음 단어 y(t)y(t) 에 대해 교차 엔트로피를 사용해서 손실함수를 적용한다.
    4.그리고 모든 손실에 대해 평균을 적용한다.
    => overall loss
  • 역전파
    Q. 반복되는 행렬인 WhW_h 에 대한 Jt(θ)J_t(θ)의 미분값은 무엇인가?
    =>바로 각각의 시간동안 나타나는 Wh에 대한 미분의 합이다.

문제

  • 경사소실 문제(Vanishing gradient problem)
    ->장기기억을 하지 못함

LM task: When she tried to print her tickets, she found that the printer was out of
toner.
She went to the stationery store to buy more toner. It was very overpriced. After
installing the toner into the printer, she finally printed her ___
빈칸을 유추하지 못함

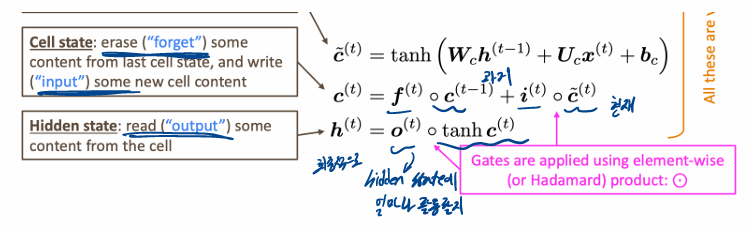
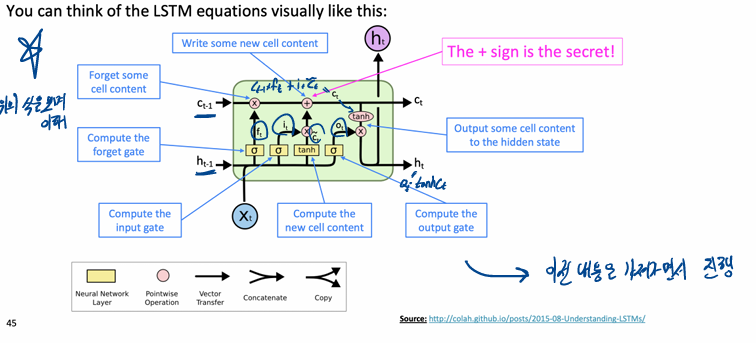
LSTM(Long Short-Term Memory RNNs)

지우거나 쓰거나 읽거나 이 셋중 하나의 선택은 gates에 의해 선택

  • forget gate : 이전 cell state를 얼마나 기억할지, 1에 가까울 수록 더 많이 기억
    ft=σ(Wf⋅[ht−1,xt]+bf)f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f)
  • imput gate : 현재 정보를 얼마나 기억할지, 1에 가까울 수록 현재 정보를 더 많이 기억
    it=σ(Wi⋅[ht−1,xt]+bi)i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)
  • output gate: 새로운 cell state를 hidden state에 얼마나 보낼지, 1에 가까울수록 많이 활용
    ot=σ(Wo⋅[ht−1,xt]+bo)o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o)

문제

=>하지만 여전히 순차적인 연산으로 장기기억을 잘 하지 못함

기계 번역에 사용

seq2seq

  • 인코더와 디코더 구조
  • 인코더: 문장->인코딩->인코딩한 마지막 hidden state를 전달
  • 디코더: ->생성될 가능성이 가장 높은 단어 예측-> 실제 단어 비교 ->손실 계산
  • 역전파로 인코더의 매개변수까지 업데이트(end to end)

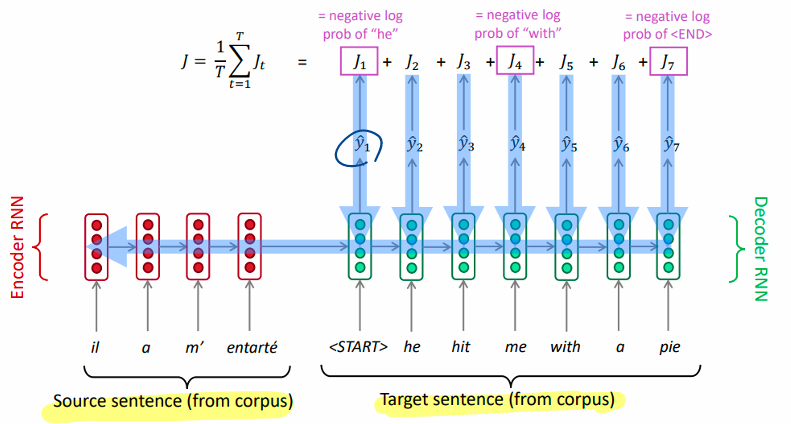
문제

  • 병목 현상 : 마지막 hidden state만 사용, 단어의 순서 등 정보의 소실이 발생
    => attention

Attenttion

장기 기억을 가능하게 하기 위해 고안됨, 단어들 사이 관계를 모두 파악

  • in seq2seq
  1. 디코더 hidden state와 인코더 hidden state를 내적
    -> attention score
    -> soft max에 넣어서 확률 분포를 구함
    -> 이 분포를 기반으로 attention output을 만듦
    -> 디코더의 hidden state와 concatenation
    -> 이를 이용해 y^\hat{y}를 구함
    • y1^\hat{y_1}
    • y2^\hat{y_2}
  • lookup table로 보기

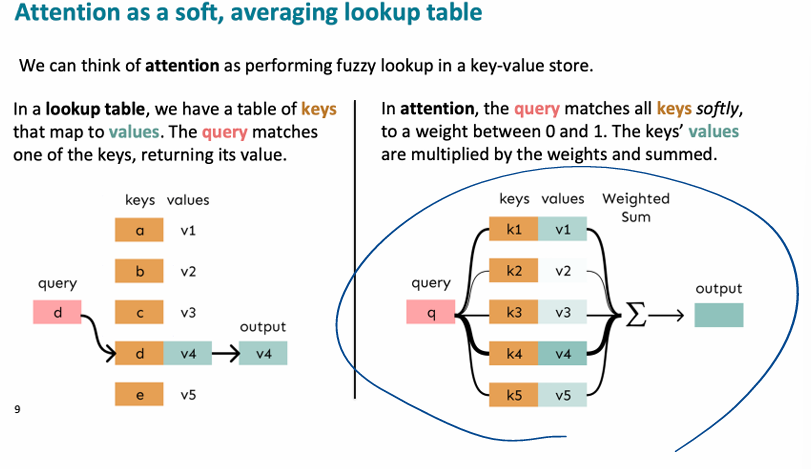
    lookup table에서 query에 맞는 keys를 선택해서 values 값을 output으로 출력하는 구조와 비슷하다.
    Attention은 살짝 다른 것이 모든 keys에 가중치를 두어 접근하고, values를 weighted sum 해서 output으로 출력하는 것이다.

    seq2seq로 따지면)
    q=디코더 hidden state,
    k=인코더의 hidden state들,
    attention scores= qxk,
    output=attention output = softmax(attention scores) x v

self-Attention

  • 차이: 같은 시퀀스(입력문장 내)에서 Q,K,V를 추출
    (기존: 디코더의 hidden state를 통해 쿼리가 생성)
  • 목적: 한 단어가 다른 모든 단어와 어떤 관계를 가지는지에 대한 정보를 가지고 가기 위함
  • 단계

  1. 각 단어의 임베딩된 벡터 xix_i (=1xd)

  2. 입력 임베딩 행렬: X=[x1,x2,…,xn]X = [x_1, x_2, \ldots, x_n] (=nxd)

  3. Q,K,VQ,K,V= XX WQ(,WK,WVW^Q(,W^K,W^V) (=nxdkd_k)

    • WQ/K/VW^Q/^K/^V (=dxdkd_k)는 모든 단어벡터에 동일하게 곱해짐
    • QQ,KK,VV는 단어 별 q,k,v 벡터들을 모아 둔 것
      Q=[q1,q2,…,qn](n×dk)Q = [q_1, q_2, \ldots, q_n] \quad (n \times d_k)
      K=[k1,k2,…,kn](n×dk)K = [k_1, k_2, \ldots, k_n] \quad (n \times d_k)
      V=[v1,v2,…,vn](n×dv)V = [v_1, v_2, \ldots, v_n] \quad (n \times d_v)

  4. Attention score\text{Attention score} =QKTQK^T(=nxn)

    • 이때 (nxn)행렬의 원소 (i,j)(i,j)는 ii번째 단어의 쿼리 벡터와 jj번째 단어의 키 벡터를 내적한 값
      즉, ii번째 단어와 jj번째 단어 사이 정보

  1. Attention Weights=softmax(QKTdk)\text{Attention Weights} = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)

  2. Attention Outputi=Attention Weights⋅V\text{Attention Output}_i = \text{Attention Weights} ⋅ V (nxdk)d_k)

    • 각 행은 각 단어들의 새로운 벡터
      (Self-Attention을 통해 문맥적으로 업데이트된 새로운 벡터)

* 나중에 잔차연결을 위해 d=dkd_k로 둠

self-Attention의 단점, 필요한 방법들

1. 순서 정보 부재

단어 사이 관계 정보는 있지만, 순서에 대한 정보가 없음
=> Add position embeddings :입력 시퀀스의 각 단어 벡터에 위치 정보를 추가

2. 비선형성 부재

Self-Attention 메커니즘에서는 입력 벡터 간의 관계를 학습하는 과정에서 비선형성을 적용되지 않음
=> feed-forward network : Self-Attention된 입력 벡터에 대해서 선형 변환을 취하고 ReLU를 통해 비선형 변환

FF 수식
mi=MLP(outputi)=W2∗ReLU(W1outputi+b1)+b2m_i =MLP(output_i ) =W_2 ∗ ReLU(W_1 output_i +b_1 )+b_2

  • output𝑖:output_𝑖 : Self-Attention 레이어의 출력
  • 𝑊1,𝑊2:𝑊_1,𝑊_2: 학습 가능한 가중치 행렬
  • b1,b2:b_1,b_2: 학습 가능한 바이어스 벡터
  • ReLU:ReLU: 비선형 활성화 함수

3. Decoder에서 실행 시

만약 self-attention을 decoder에 실행하기 위해서는 우리는 그 다음 단어를 고려하지 않고 실행해야 한다.
why?
->다음에 올 단어를 예측하는 걸 배워야하기 때문에!
->단어 벡터에 다음에 올 단어들과의 관계 정보를 추가하면 학습 목표와 맞지 않음
=> masked attention: 마스킹을 통해서 미래의 단어를 제외하고 attention을 진행(자기 자신 이전 단어들과의 관계만 사용함)

4. attention을 수행 할 때마다 결과가 달라짐

attention을 수행 할 때마다 그 결과가 달라질 수 있다.

ex) 첫번째 Attention의 경우에는 의미론적으로 접근했지만, 두번째 Attention의 경우에는 구문론적으로접근

=> multi-head Attention : Self-Attention 연산을 여러 번 수행하고, 그 결과를 결합하는 방식

  • 과정

  1. Qi,Ki,ViQ_i, K_i, V_i 벡터 생성 (각 헤드마다)

    Qi=XWiQ,Ki=XWiK,Vi=XWiVQ_i = X W_i^Q, \quad K_i = X W_i^K, \quad V_i = X W_i^V

    이 과정은 WiQ,WiK,WiVW_i^Q,W_i^K,W_i^V 를 각 헤드마다 달리해서, 독립적으로 수행
    *point) 인풋은 그대로, 가중치만 헤드마다 달라짐

  2. Self-Attention 연산 (각 헤드마다)

    Attention Scoresi=QiKiTdk\text{Attention Scores}_i = \frac{Q_i K_i^T}{\sqrt{d_k}}
    Attention Weightsi=softmax(Attention Scoresi)\text{Attention Weights}_i = \text{softmax}(\text{Attention Scores}_i)
    Headi=Attention WeightsiVi\text{Head}_i = \text{Attention Weights}_i V_i

    각 헤드는 자신만의 쿼리, 키, 값 벡터를 사용하여 Self-Attention 연산을 수행
    각 헤드는 크기가 dk/hd_k/h인 어텐션 출력을 생성

  3. 헤드 결합 (Concat)

    Multi-Head Output=Concat(Head1,Head2,…,Headh)WO\text{Multi-Head Output} = \text{Concat}(\text{Head}_1, \text{Head}_2, \ldots, \text{Head}_h) W^O

    각 헤드의 출력을 결합(dk/hd_k/h출력 h개 합침)
    *여기서 WOW^O는 결합된 출력을 변환하는 데 사용되는 학습 가능한 가중치 행렬

Transformer

"self attention과 위의 네가지 방법을 이용해 만든 encoder decoder 모델이 transformer"
+)트랜스 포머는 seq2seq의 한 종류

아키텍처

  • Add & Norm : Residual connections & Layer normalization
    • xi=xi−1+Layer(xi−1)x_i= x_{i−1} + Layer(x_{i-1} )
    • x^i=xi−μσ2+ϵ\hat{x}_i = \frac{x_i - \mu}{\sqrt{\sigma^2 + \epsilon}}
    • LayerNorm(x+layer(x))LayerNorm(x+layer(x))
    • 연결을 위해 d=dkd_k로 둠
  • cross-attention
    • 디코더의 입력 XdecX_{dec} 로부터 QQ를 생성하고,
    • 인코더의 출력 HencH_{enc}로부터 KK와 VV를 생성
    • Q=XdecWQ,K=HencWK,V=HencWVQ = X_{\text{dec}} W^Q, \quad K = H_{\text{enc}} W^K, \quad V = H_{\text{enc}} W^V

단계 별 행렬의 형태

  • 출력 벡터는 1xV(첫번째 행 사용), 2xV(두번째 행 사용), 3xV(세번째 행 사용),,,,,의 형태
    • 단어 V개의 어휘집
  • 첫번째 시행의 경우

디코더의 예측

  • <'s'>로 시작해 한 단어씩 다음 단어를 예측해 나가며, 이전 시행에서 예측한 output을 디코더의 인풋으로 받음
  • 가져온 어휘집(V개의 단어)에서 높은 확률을 가지는 단어를 선택(기본)
  • 빔서치를 사용

최근기술

"한번에 넣고 한번에 출력받을 순 없나?"

  • 디코더 입력:<시작 토큰> <"I"> <"want"> <"you"> 모두 넣음
  • 정답: <"I"> <"want"> <"you"> <"종료 토큰">

-> 입력 첫번째 토큰의 정답 = 정답의 첫번째 토큰 가능해짐

문제) "그럼 어텐션 시 뒷 단어와의 관계까지 들어가는데??"
-> 어텐션 시 뒷단어와의 관계를 없애자
masked multihead Attention:
QKTQK^T [(4xd)(dx4)=(4x4)] 는 앞에서 설명했듯이, 행렬의 원소들이 단어들 사이 정보를 담고있음
=>이 행렬에 masking을 함 = 뒷 단어와의 관계 원소엔 음의 무한대를 곱해줌
=> Attention Weights⋅V\text{Attention Weights} ⋅ V {(3x3)(3xd)=(3xd)}
= 각 단어 벡터들이 (마스킹한) 각 단어 사이 정보를 담고 있는 벡터로 바뀜

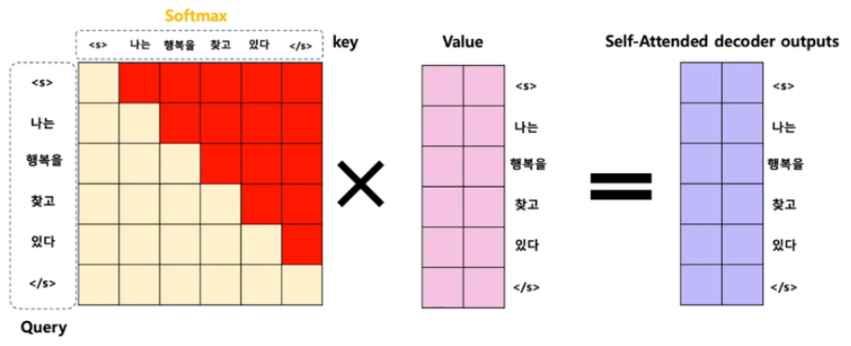
전체과정)

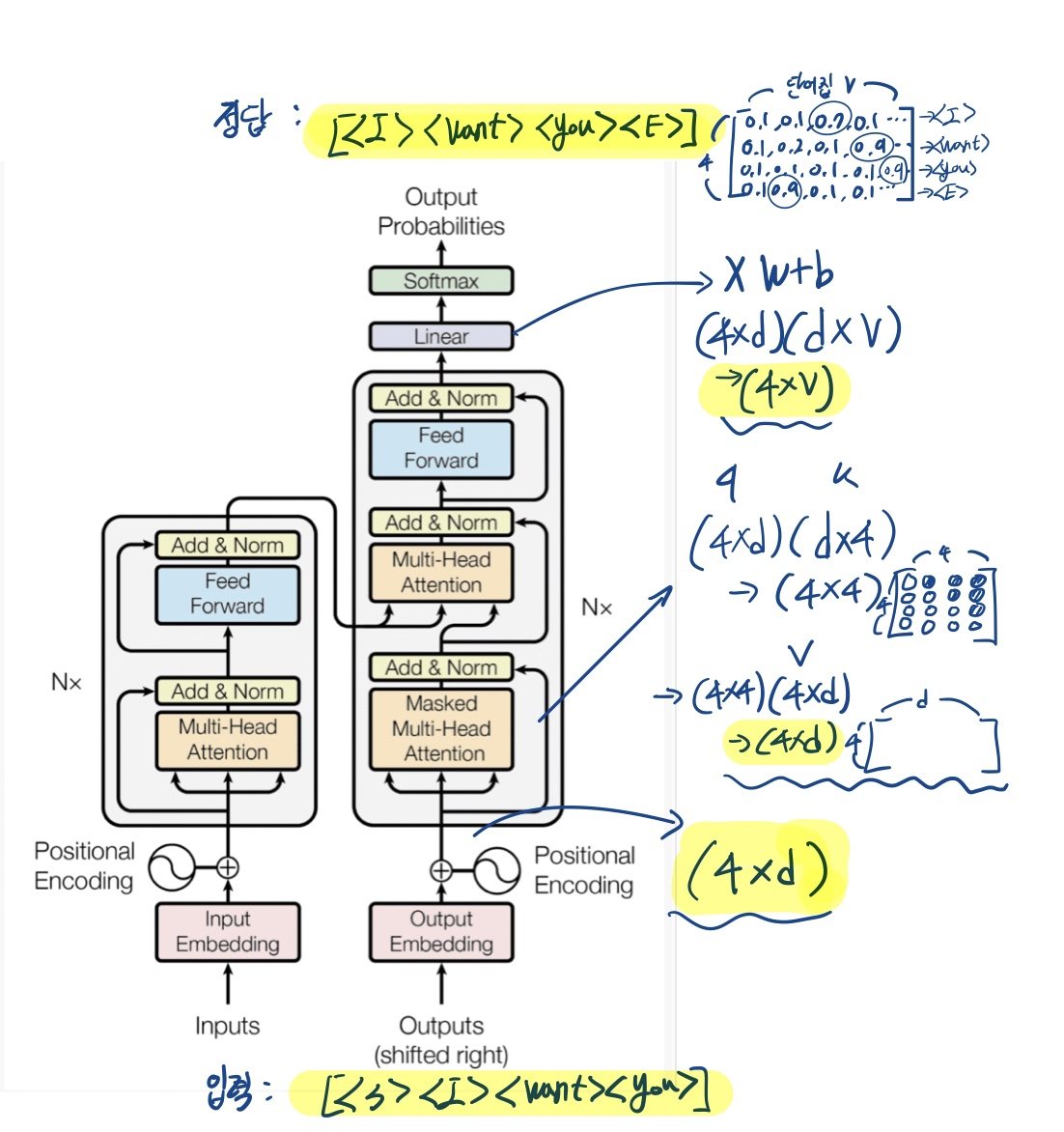
=>그럼 빔서치는 사용???

  • 훈련
    입력 시퀀스 전체에 대해 예측을 수행한 후 손실을 계산하고 가중치를 업데이트
    그 다음 입력 시퀀스에 대해 동일하게 반복

    전체 손실: Ltotal=L1+L2+L3+L4L_{total} = L1+L2+L3+L4 (네 개의 단어로 이뤄진 문장일때)

    예시)
    배치1:["I am a student", "She is a teacher"]
    ->예측->손실 계산->가중치 업데이트
    배치2:["They are engineers", "We are learners"]
    ->예측->손실 계산->가중치 업데이트
    =>반복

    • Adam 사용
    • 드롭아웃 적용
    • 라벨 스무딩

  • 예측
    디코더가 출력을 내보내는 방식 그대로 출력

  • 결론

    이전 모델과 단순 비교
    > 1. 계산 복잡도 (Computational Complexity):
    -자기 어텐션 층의 계산 복잡도는 O(n2⋅d)O(n^2⋅d)로, 시퀀스 길이 nn이 표현 차원 dd보다 작을 때 순환 층보다 빠름
    *주위 rr개의 단어만 사용하면 O(r⋅n⋅d)O(r⋅n⋅d) but path 가 늘어남
    2. 병렬화 가능성 (Parallelization)
    -자기 어텐션 층은 모든 위치 간의 연산이 병렬로 수행될 수 있어 순차 연산 수가
    O(1)O(1)
    -순환 층은 순차적인 특성으로 인해 O(n)O(n) 순차 연산이 필요
    3. 경로 길이 (Path Length):
    '짧을 수록 유리'
    -자기 어텐션 층은 모든 위치 간의 경로 길이가 O(1)O(1)로 일정
    -순환 층은 경로 길이가O(n)O(n)이며, 이는 장거리 의존성을 학습하는 데 불리
    -컨볼루션 층은 커널 크기 k에 따라 경로 길이가 logk(n)log_k(n)로 다름

    영어-독일어(EN-DE)와 영어-프랑스어(EN-FR) 번역 작업에 대한 BLEU 점수와 학습 비용을 비교

  • 높은 점수와 낮은 계산비용

    트랜스포머 아키텍처의 변형

    • head 수와 차원: 너무 많은 헤드는 품질을 저하시킬 수 있으며, 최적의 설정이 필요합니다.
    • k 차원 크기: k 차원 크기를 줄이면 품질이 저하될 수 있습니다.
    • 모델 크기: 큰 모델은 일반적으로 더 나은 성능을 제공합니다.
    • 드롭아웃: 적절한 드롭아웃 비율은 과적합을 방지하고 성능을 향상시킬 수 있습니다.
    • 위치 인코딩: 사인 곡선 위치 인코딩과 학습된 위치 임베딩은 거의 동일한 성능을 보입니다.

    문장 구조 분석에 사용

    • 과제별 튜닝이 부족함에도 불구하고, 모델이 놀라울 정도로 잘 수행

질문) 마스킹을 사용하지 않고 지금까지 예측된 단어들 간 정보를 모두 사용하면
즉, 두번째 단어 벡터에 세번째 단어 벡터와의 관계 정보까지 포함 시키면, 이전 단어와 다음단어 간의 정보가 더 풍부해질 것
->이러한 정보를 가지고 학습하면,
이러한 정보 아래 다음 단어를 추측하는 능력이 생기고,
추론시에서 이 정보를 활용해 더 잘 추론하지 않을까?

profile
YONG
이전 포스트

AAC

다음 포스트

CNN

0개의 댓글