자, 스물 두 번째인 '구면좌표계'를 알아볼 것이다.

이번엔 구면좌표계와 연관된 키워드도 같이 알아보았다.

구면 좌표계가 뭐에요?

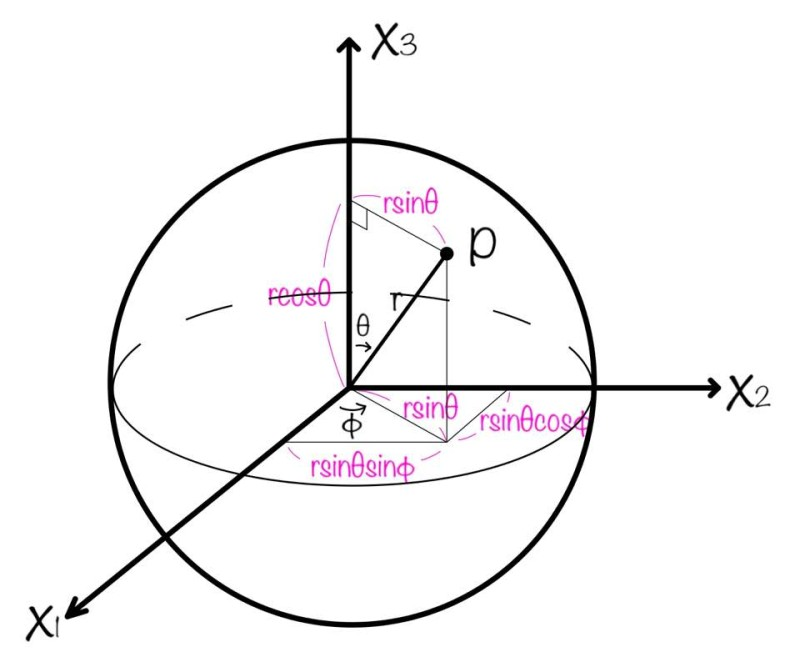
구면 좌표계는 3차원 공간에서 점을 나타내는 좌표 체계 중 하나이다. 이 좌표 체계는 구를 기반으로 하며, 일반적으로 구면 좌표계에서 사용되는 구는 구면 좌표계를 가장 잘 설명할 수 있는 구 형태인 구면좌표계 공간 구조를 갖는다. 구면 좌표계는 일반적으로 공간에서의 점의 위치를 세 개의 값 (반지름, 방위각, 고도)으로 나타낸다.

여기서 세 가지 주요 구성 요소는 다음과 같다.

1. 반지름 (Radius): 구면 좌표계에서의 반지름은 구의 중심에서 점까지의 거리를 나타낸다. 이것은 구면 좌표계에서의 점의 위치를 나타내는 기본적인 구성 요소이다.

2. 방위각 (Azimuth): 방위각은 구의 중심을 기준으로 0°부터 360°까지의 각도로 나타내며, 특정 축 (일반적으로 x축)을 따라 측정된다. 이 각도는 점이 구의 중심을 기준으로 얼마나 돌아가 있는지를 나타낸다.

3. 고도 (Elevation): 고도는 구의 평면에 대한 각도로, 일반적으로 구의 중심과 특정 점을 연결하는 선이 구의 평면과 이루는 각도를 의미한다. 이 각도는 구의 평면을 따라 위아래로 측정된다.

이러한 세 가지 구성 요소를 결합하여 구면 좌표계에서의 한 점의 위치를 정확하게 나타낼 수 있다. 이러한 구면 좌표계는 대기 과학, 천문학, 지리학 등 다양한 분야에서 사용되며, 특히 지구나 다른 천체의 표면을 설명하는 데 유용하다고 한다.

오일러와 라디안의 관계

오일러와 라디안은 수학 및 공학 분야에서 중요한 개념이다. 오일러(Euler)는 18세기의 스위스 수학자이며, 라디안(radian)은 각도의 측정 단위 중 하나이다.

1. 라디안 (Radian):
   라디안은 호의 길이와 반지름의 길이의 비율로 정의된다.
   1 라디안은 반지름과 호 사이의 길이가 반지름의 길이와 같은 원의 호에 해당한다.
   1 라디안은 약 57.3도에 해당한다.

2. 오일러의 공식 (Euler's formula):
   오일러의 공식은 다음과 같이 표현된다. e iθ =cos(θ)+isin(θ), 여기서
   e는 자연 상수이고 i는 허수 단위이다.
   이 공식은 복소수와 삼각함수 간의 연관성을 제시한다.
   라디안과 오일러의 관계는 주로 오일러의 공식을 통해 나타낸다. 오일러의 공식에서 각도
   θ는 라디안 단위로 표현된다. 따라서 오일러의 공식을 사용할 때, 각도를 라디안으로 변환하여 사용해야 합니다. 이는 오일러의 공식을 사용하여 복소수 형태의 삼각함수를 계산할 때 흔히 사용되는 방법 중 하나이다.

라디안은 원주 위의 호의 길이를 반지름의 길이로 나눈 값으로 정의되며, 오일러의 공식은 삼각함수와 지수함수 사이의 관계를 제시한다. 이 둘을 함께 고려하면, 라디안과 오일러의 공식은 수학과 공학에서 다양한 문제를 해결하는 데 유용한 도구로 활용된다.

오일러각이란?

오일러 각은 오일러의 공식을 통해 복소 평면 상의 각도를 나타내는 개념이다. 복소수를 이용하여 각도를 표현할 때, 오일러 각을 사용하면 특정한 복소수의 크기와 각도를 쉽게 나타낼 수 있다.

복소수 z=a+bi가 있을 때, a는 실수 부분이고 b는 허수 부분이다.
이 때, z의 오일러 각은 오일러의 공식
e iθ 에서 θ에 해당하는 값입니다. 즉, θ는 z의 크기와 각도를 정의한다.

오일러 각은 주로 극좌표계나 복소수 평면에서 사용된다. 극좌표계에서, 오일러 각은 원점에서부터 복소수가 이루는 각도를 나타낸다. 복소수 평면에서는 오일러 각은 복소수를 극좌표계로 나타낼 때의 각도이다.

오일러 각은 각도를 라디안 단위로 표현할 수 있으며, 일반적으로 0에서 2π 사이의 값을 갖는다. 이는 오일러의 공식이 한 주기를 갖는 주기 함수인 삼각함수와 관련이 있다.

요약하자면, 오일러 각은 복소수를 극좌표계로 나타낼 때 사용되는 각도이며, 오일러의 공식을 통해 복소수의 크기와 각도를 쉽게 계산할 수 있도록 도와주준다.

결론 - 느낀 점

역시 수학적인 지식이 꼭 요구되는것이 게임분야인것 같다...