자 스물 여섯번째 키워드 '사원수'를 알아보겠다.

지난 키워드에 이어서 수학과 관련된 내용이므로 이론 중심으로 알아보았다.

사원수가 뭐에요?

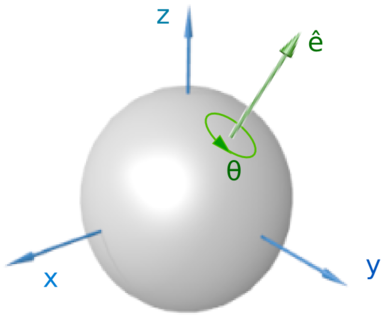
자 유니티를 다뤄본 사람으로서 사원수는 Quaternion으로 알고 있다. 그렇다면 사원수라는 것은
무엇일까?

해밀턴 회로를 발견한 아일랜드의 수학자 윌리엄 로원 해밀턴이 창시한 수의 체계라고 한다.
복소수가 허수 단위인 i를 도입했듯이 새로운 단위 j, k를 도입한 것이다.
복소수를 도입할 때 x^2 = -1 이라는 대수 방정식의 해로 허수 i를 정의 했는데,
관점을 살짝 다르게 하여 i와는 다르지만 j^2 = -1 인 수를 추가하여 3차원 공간을 표현하는
수를 만들고자하여 출발 한 것이 사원수이다.

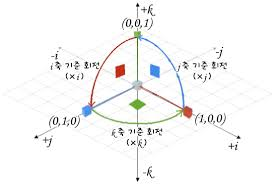
이전에 알아본 복소수가 평면의 회전을 나타내는 데 쓰이는 반면 사원수는 공간에서의 회전을
나타내는데 쓰인다.

사원수의 활용

컴퓨터 애니메이션 분야에서 자주로 사용이 되며 효율적으로 사용중이라고 한다.
왜냐하면 기존에 사용하던 오일러 각 체계를 사용할 때 짐벌 락 현상이 발생했는데
사원수를 활용하면 짐벌락 현상을 없앨 수 있었기 때문이다.

결론 - 느낀 점

확실히 쿼터니언을 다뤄 보았지만 수학적인 개념으로 접근하니 매우 어려운 개념이었다.

하지만 확실히 알고 간 것은 짐벌락에 대한 개념과 유니티에서 오일러및 사원수의 개념을
둘다 사용하고 있는 점이다.

수학은 이해가 되면 정말 좋겠지만 안되는것만큼 고통스러운게 없는 것 같다.