파이썬 반올림 이상해요

파이썬에서 반올림의 결과를 리턴하는 round 함수는 수학에서 배웠던 것과 조금 다르게 동작한다.

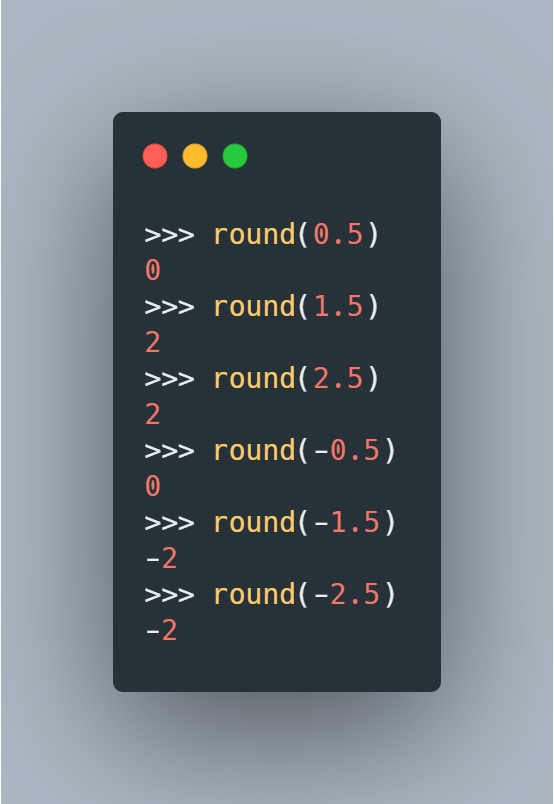
1.5, 2.5 모두 반올림의 결과로 2를 리턴했다. 초등 수학에서 배웠던 개념으로 생각하면, 둘 다 올림 처리가 되어야 하는 것이 맞다. round(1.5)는 2, round(2.5)는 3의 결과를 가져야 타당하다.

어림(근사)

어림(근사)은 근사 처리되어야 할 대상, 예를 들어 1.15를 정수로 근사할 때 0.15를 처리하는 방법에 대한 개념이다. 그 방법에는 올림, 버림, 반올림이 있다.

올림과 버림은 자리 올림이 진행될 때 변위가 모두 동일한 방향을 갖는 Directed Rounding에 속한다. 예로 올림은 변위가 +∞를 향하고, 버림은 변위가 -∞을 향한다. 파이썬의 round 함수는 변위의 방향이 하나로 정해지지 않으므로(e.g. 0.5 -> 0(변위 -0.5), 1.5 -> 2(변위 +0.5)) 여기에 해당되지 않는다.

반올림

반올림은 근사의 과정에서 올림을 하기도 하고, 버림을 하기도 하는 방식이다. 반올림의 예로 대표적인 사사오입 방식을 예로 들면, 근사 처리되어야 할 대상이 0.5, 0.6처럼 절반 이상일 때 올리고, 0.3, 0.4처럼 절반 미만일 때 버리게 된다.

그러나, 프로그래밍에서 사사오입과 같은 맹목적인 올림 처리는 적절하지 않은 것으로 간주한다. 예로 소수부가 0.5인 숫자들로 이루어진 데이터셋을 처리한다고 가정하자. 사사오입 방식을 사용하는 경우, 반올림 처리되기 전과 후의 집계 결과에 오차가 커질 수 있다.

• [0.5, 1.5, 2.5, 3.5]라는 List의 요소를 모두 더한 결과는 8이다.
• 모든 요소를 사사오입 방식으로 반올림 처리한 뒤 모두 더하면 1 + 2 + 3 + 4로 10이 된다.

4개의 요소들이 모두 0.5만큼 고평가되어, 결과적으로 2의 오차가 생겼다. 이런 문제로, 공학에서는 통계학적으로 더 합리적인 반올림 방법들을 사용하곤 한다. 사사오입은 반올림의 방식 중 하나라는 것을 인지하자.

반올림의 모든 방식들은, 근사로 처리될 대상이 정확히 절반에 해당하는 경우를 어떻게 처리할지에 대한 고민에서 출발한다. 0.5를 반올림했을 때 1이 된다는 것이 너무 당연하다고 생각할 수 있지만, 0.5가 만약 0으로 버림 처리되더라도 참값과의 오차는 올림 처리된 1 0.5로 동일하다.

부동 소수점의 연산에 관한 표준을 다루는 IEEE 754에서는, 이런 오차를 보정해주기 위한 반올림 방법으로 Round half to even을 제시한다.

Round half to even

반올림 대상이 절반에 걸리는 경우 가까운 짝수로 맞춰준다. 0.5는 0, 1.5와 2.5는 2가 되는 식이다. IEEE 754가 기본값으로 추천하는 방식으로, 파이썬의 round 함수도 이 방식을 사용하고 있다. Bankers' rounding, Gaussian rounding이라 부르기도 한다.

여담

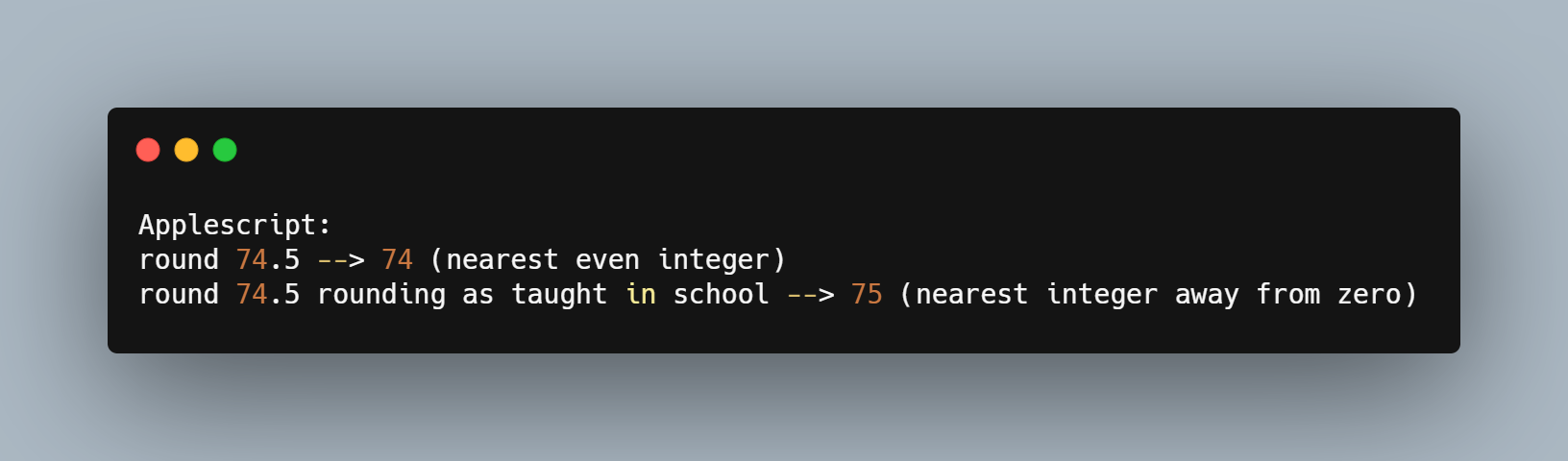
AppleScript에는 rounding as tought in school이라는 커맨드가 있다.