먼저, 힙에 대해 알기 위해 완전 이진 트리와 힙의 상관관계를 알아두면 좋다.
완전 이진 트리란?
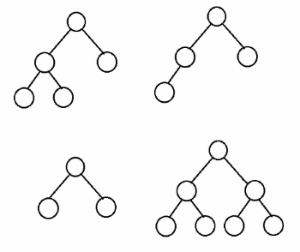
완전 이진 트리는 트리에서 마지막 레벨 이전의 모든 레벨이 가득 차 있고, 마지막 레벨(깊이)에만 노드가 왼쪽부터 오른쪽으로 순차적으로 채워지고 있는 트리를 뜻한다.
힙
힙은 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기 위해 고안된 완전이진트리를 기본으로 한 자료구조로서 다음과 같은 속성을 만족한다.
-
A가 B의 부모노드(parent node) 이면, A의 키(key)값과 B의 키값 사이에는 대소관계가 성립한다.
-
부모노드의 키값이 자식노드의 키 값보다 항상 큰 힙을 '최대 힙', 부모노드의 키 값이 자식노드의 키 값보다 항상 작은 힙을 '최소 힙'이라고 부른다.
-
힙에서는 가장 높은(혹은 가장 낮은) 우선순위를 가지는 노드가 항상 뿌리노드에 오게 되는 특징이 있으며, 이를 응용하면 우선순위 큐와 같은 추상적 자료형을 구현할 수 있다.
[최대 힙의 예시]
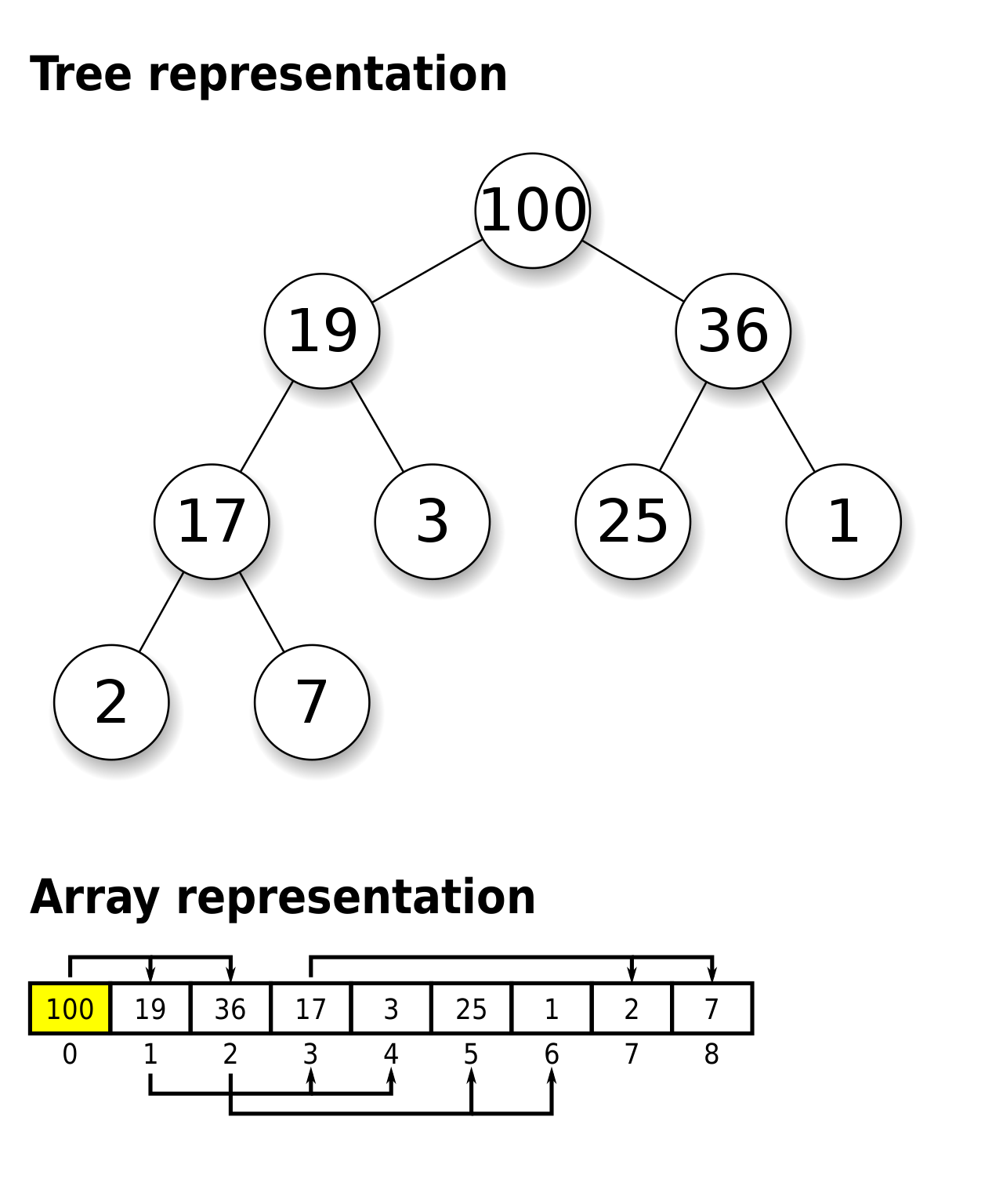
JS로 구현
- 먼저 아래 MaxHeap 이라는 클래스의 배열이 이진 트리를 그린다고 생각해보자.
class MaxHeap {
constructor() {
this.heap = [];
}
getParentIndex(index) {
return Math.floor((index - 1) / 2);
}
getLeftChildIndex(parentIndex) {
return 2 * parentIndex + 1;
}
getRightChildIndex(parentIndex) {
return 2 * parentIndex + 2;
}- 부모의 인덱스는 Math.floor((자식의 인덱스 - 1) / 2)
- 왼쪽 자식의 인덱스는 2 * parentIndex + 1
- 오른쪽 자식의 인덱스는 2 * parentIndex + 2
- 다음으로 구현할 부분은 삽입이다.
insert(value) {
this.heap.push(value);
let index = this.heap.length - 1; // 2-1. 삽입된 마지막 노드의 인덱스
let parentIndex = getParentIndex(index); // 2-2. 부모 노드의 인덱스
// 2-3
while (index > 0 && this.heap[parentIndex] < this.heap[index]) {
// 2-4
[this.heap[parentIndex], this.heap[index]] = [this.heap[index], this.heap[parentIndex]];
// 2-5
index = parentIndex;
// 2-6
parentIndex = getParentIndex(index);
}2-1. 삽입한 값이 배열의 맨 끝에 위치하므로, 시작 인덱스를 this.heap.length - 1로 설정합니다.
2-2. 자신의 값과 부모의 값을 비교해야하기 때문에, 부모 노드의 인덱스를 찾습니다.
2-3. 새로 삽입된 노드가 루트 노드가 아니고(index > 0), 그 값이 부모의 값보다 크다면, 정렬을 실시합니다. (자식 노드끼리는 대소를 비교하지 않기때문에 가능합니다.)
2-4. (상세한 정렬 구현부) 부모 인덱스와 자신 인덱스의 값 교환
2-5. 다시 while 루프를 돌리기 위해 자신의 인덱스를 업데이트 해줍니다.
2-6. 다시 while 루프를 돌리기 위해 부모의 인덱스도 업데이트 해줍니다.
- 마지막으로 구현해 볼 부분은 삭제이다!
removeMax() {
// 노드가 없거나 하나뿐이라면, 빈 배열을 출력해준다.
if (this.heap.length <= 1) {
this.heap = [];
return this.heap;
}
// 어떤 값을 제거했는지 알려주기 위해 제거하기 전, 값을 저장해둔다.
const max = this.heap[0];
// 3-1
this.heap[0] = this.heap.pop();
// 3-2
let index = 0;
// 3-3
while (this.heap[this.getLeftChildIndex(index)] !== undefined) {
// 3-4
let largerChildIndex = this.getLeftChildIndex(index);
if (
this.heap[this.getLeftChildIndex(index)] !== undefined &&
this.heap[this.getRightChildIndex(index)] >
this.heap[this.getLeftChildIndex(index)]
) {
largerChildIndex = this.getRightChildIndex(index);
}
// 3-5
if (this.heap[index] > this.heap[largerChildIndex]) {
break;
} else {
[this.heap[index], this.heap[largerChildIndex]] = [
this.heap[largerChildIndex],
this.heap[index],
];
}
index = largerChildIndex;
}
// 반복문 종료
// 3-6
return max;
}3-1. 힙 자료구조 에서는 최대 힙이든 최소 힙이든 루트 노드를 항상 먼저 삭제한다.
3-2. 루트 노드를 제거했으므로 index에 0으로 두고 while 반복문을 실행한다.
3-3. 자식 노드가 존재하는 경우에만 반복문을 실행한다. (왼쪽 자식 노드부터 채워지기 때문에, 오른쪽 자식 노드는 검사하지 않아도 된다.
3-4. 일단 왼쪽 자식의 값으로 더 큰 값을 초기화해두고, if문을 통해 오른쪽 노드가 존재하면 비교해서 더 큰 값을 largerChildIndex 변수에 둔다.
3-5. 현재 노드의 값이 자식의 최대값보다 크다면 반복문을 종료합니다. 그렇지 않다면, 두 값을 바꿔주고 인덱스를 업데이트 해주고 3-1로 돌아가 다시 반복문을 실행합니다.
3-6. 제거한 노드의 값을 return 합니다.
