참고자료
- 네트워크 유량(Network Flow) - 기내식은수박바
가장 이론적인 부분을 잘 설명한 것 같다.- 네트워크 유량(Network Flow) (수정: 2019-08-14) - 라이
가장 친절하고 자세하고 재밌게 설명한다.- [네트워크 유량] Network Flow(최대 유량, 최소 컷) 알고리즘 - EVEerNew
심플하게 잘 정리되어있다.- [Algorithm] 네트워크 유량(Network Flow) - 새로비
파이썬 코드 예제와 함께 구현 방법에 집중한 글이다.
용어
-
네트워크 유량 : 그래프에서 출발지 A에서 도착지 B까지 얼마나 많은 유량 또는 흐름을 보낼 수 있는지 계산하는 알고리즘
-
소스(Source) : 유량이 시작되는 정점 (출발 정점)
-
싱크(Sink) : 유량이 도달하는 정점 (도착 정점)
-
용량(Capacity) : c(u, v) - 정점 u에서 정점 v로 흐를 수 있는 흐름의 최대 양 (단방향 가중치)
-
유량(Flow) : f(u, v) - 정점 u에서 정점 v로 현재 흐르고 있는 흐름의 양
-
잔여용량 : r(u, v) - 정점 u에서 정점 v로 추가로 흐를 수 있는 흐름의 양
- 용량 - 유량으로 구할 수 있다.
-
증가경로 : 소스에서 싱크에 도달하는 경로
개념
-
용량 제한 : 각 간선은 용량을 넘어서는 유량이 흐를 수 없다.
- 즉 잔여 용량이 남아있는 간선에만 새로운 흐름이 생길 수 있다.
-
유량의 대칭성 : u -> v로 n의 유량이 흐른다면, v입장에서는 v -> u로 -n의 유량이 흐르는 것과 같다.
f(v, u)=-f(u, v)
-
유량 보존 : 모든 정점에서 흘러오는 유량과 나가는 유량은 동일하다. 유량의 대칭성에 의해 나가는 유량은 음수이므로 합은 항상 0이 된다.
- 소스와 싱크는 예외이다.
에드몬드-카프 알고리즘
- 소스에서 싱크로 흐를 수 있는 최대 유량을 구하는 알고리즘이다.
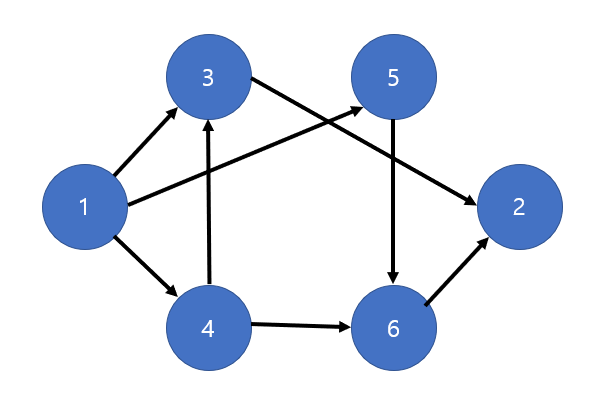
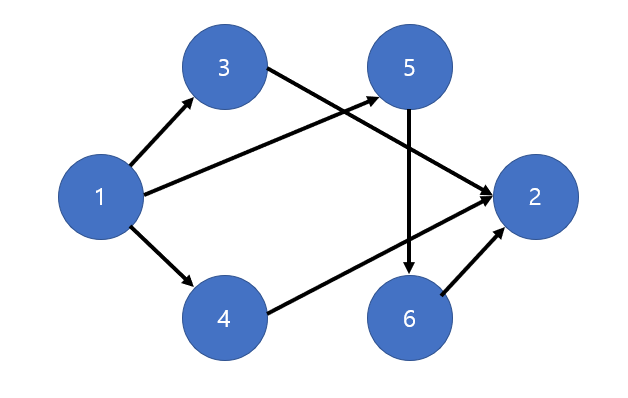
다음과 같은 유량 그래프가 있다고하자
- 모든 간선의 용량은 1이라고 한다.
- 소스는 1, 싱크는 2이다.
알고리즘 절차
-
sink 까지의 길을 탐색하자 BFS와 DFS를 사용하여 탐색하면 되는데 DFS는 일부 데이터에서 불리할 수 있다
-
BFS는 늘 최단경로를 찾기 때문인데, 알고리즘을 알기위해 우선 DFS로 탐색을 한다고 가정하자.
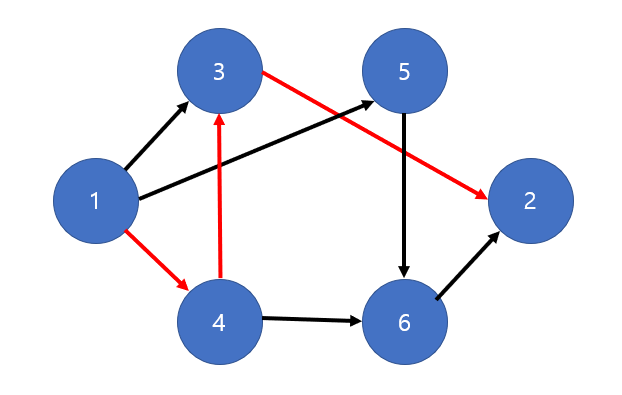
- DFS로 1 -> 4 -> 3 -> 2의 경로를 찾아 내었다.
- 1 -> 4의 용량은 1 유량은 0이므로 잔여 용량 = 1 - 0 = 1
- 4 -> 3의 용량은 1 유량은 0이므로 잔여 용량 = 1 - 0 = 1
- 3 -> 2의 용량은 1 유량은 0이므로 잔여 용량 = 1 - 0 = 1
-
해당 경로에 흐를 수 있는 총 유량 역시 1이 된다. (각 간선의 잔여 용량 최솟값)
-
용량이 1이므로, 한 번 지나간 것으로 해당 간선의 잔여 용량은 0이 된다. (빨간 선 표시)
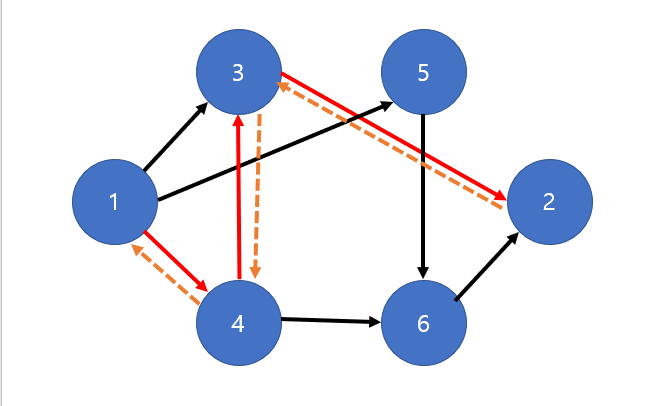
- 그리고 유량 대칭성에 의해 유량이 -1인 역방향 간선이 생성된다.
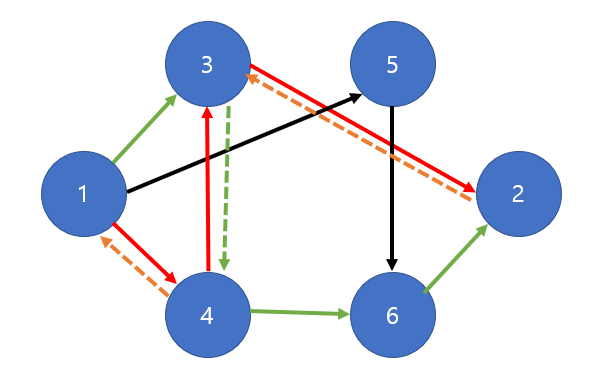
- 새로운 경로를 초록색으로 표시하였다.
- 1 -> 3의 용량은 1 유량은 0이므로 잔여 용량 = 1 - 0 = 1
- 3 -> 4의 용량은 0 유량은 -1이므로 잔여 용량 = 0 - (-1) = 1
- 4 -> 6의 용량은 1 유량은 0이므로 잔여 용량 = 1 - 0 = 1
- 6 -> 2의 용량은 1 유량은 0이므로 잔여 용량 = 1 - 0 = 1
- 3 -> 4 경로가 바로 유량 대칭성의 핵심으로, 원래라면 없는 간선(=용량 0)이지만 용량 대칭에 의해 생성된 음의 유량을 갖는 간선이다.
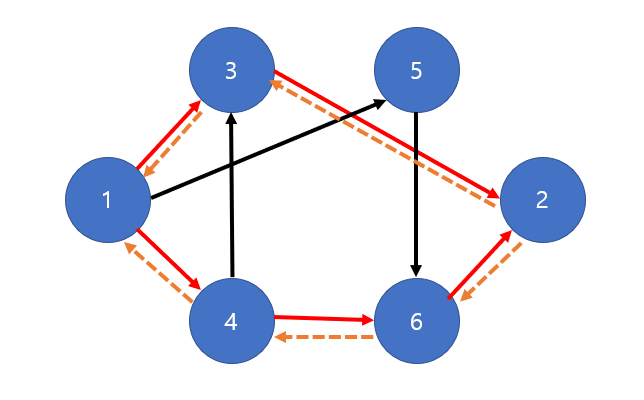
-
4 -> 3 간선은 용량 1, 유량 1로 잔여 유량이 0이었지만, 유량 대칭성에 의해 -1의 유량이 흘러 유량 0이 되었다. (빨간색 화살표 -> 검정색 화살표)
-
반대로 첫 경로에서 생성된 3 -> 4의 용량 0 유량 -1 간선은, 유량이 1 추가되어 유량 0이 되었다. (점선 화살표가 사라짐)
-
이제 가능한 경로는
1 -> 5 -> 6 -> 4 -> 3정도가 있는데, 싱크에 도달하지 못하는 경로이므로 탐색을 종료한다.
결론 정리
최종 탐색된 경로는 다음의 2개이다
1 -> 4 -> 3 -> 21 -> 3 -> 4 -> 6 -> 2

그런데 처음 그림을 보면 1 -> 3 -> 4 -> 6 -> 2는 불가능한 경로이다.
이는 3-4 사이에 유량이 유량대칭성에 의해 상쇄되었기 때문이다.
실제로는
1 -> 3 -> 21 -> 4 -> 6 -> 2
이 두가지 경로를 지난 것 과 같다.
이는 에드몬드-카프 알고리즘을 통해 소스에서 싱크로 가는 최대 유량(유량이 1이니 곧 최대 경로의 수)를 찾은 것이다.
구현에 집중하느라 자세한 원리는 설명하지 못했는데
사실 나도 완전히 잘 이해하지 못했다...
반복 연습하면서 익히는 것이 최선일 것 같다.
백준 연습문제
1. 단방향 그래프 - 17412. 도시 왕복하기
문제 : 도시 왕복하기 1
위에 설명한 알고리즘 그대로 전체 간선의 용량이 1인 네트워크 용량 문제이다.
import sys
from collections import deque
input = sys.stdin.readline
INF = 2147000000
MAX_N = 401
answer = 0
# 경로 탐색 알고리즘
def BFS(source, sink, visited):
que = deque()
que.append(source)
while que and visited[sink] == -1:
sv = que.popleft()
# 잔여용량이 있을 때만 해당 경로로 탐색 및 방문 체크
for dv in graph[sv]:
if capacity[sv][dv] - flow[sv][dv] > 0 and visited[dv] == -1:
que.append(dv)
visited[dv] = sv
# 싱크 정점에 도달 했을 때 빠져 나옴
if dv == sink:
break
# 경로를 다 돌았는데 싱크를 못찾았을 경우 탐색 종료
if visited[sink] == -1:
return True
else:
return False
def edmonds_karp(source, sink):
answer = 0
while True:
visited = [-1 for _ in range(MAX_N)]
if BFS(source, sink, visited):
break
min_flow = INF
# 탐색한 경로를 되짚어가면서 경로에 흐를 수 있는 유량을 구함 (이 문제에서는 무조건 1)
j = sink
while j != source:
i = visited[j]
min_flow = min(min_flow, capacity[i][j] - flow[i][j])
j = i
# 증가 경로는 유량 추가, 그리고 역방향으로 음수 유량을 추가 함
j = sink
while j != source:
i = visited[j]
flow[i][j] += min_flow
flow[j][i] -= min_flow
j = i
# sink로 도달한 유량 총량 저장
answer += min_flow
return answer
N, P = map(int, input().split())
graph = [[] for _ in range(MAX_N)]
capacity = [[0]*MAX_N for _ in range(MAX_N)]
flow = [[0]*MAX_N for _ in range(MAX_N)]
for _ in range(P):
sv, dv = map(int, input().split())
graph[sv].append(dv)
graph[dv].append(sv) # 음의 유량을 고려해서 양방향으로 추가함
capacity[sv][dv] = 1
print(edmonds_karp(1, 2))2. 양방향 그래프 (2316 - 도시 왕복하기 2)
문제 : 도시 왕복하기 2
-
양방향 그래프가 주어진 문제이다.
-
에드몬드-카프 알고리즘의 경우 모든 흐름을 u -> v로 간주하기 때문에, 양방향 그래프는 별도로 처리해야 한다.
-
흐름이 들어오는 정점, 흐름이 나가는 정점으로 분리해서 N * 2개의 정점을 생성하고 모든 간선을 단방향으로 처리해야 한다.
-
처리만 잘 해주면 알고리즘 구현 부분은 단방향 그래프와 동일하다.
참조 : > - 네트워크 유량(Network Flow) (수정: 2019-08-14) - 라이
스크롤을 내리면 도시 왕복하기2 문제를 설명하는 그림이 있다.
import sys
from collections import deque
input = sys.stdin.readline
INF = 2147000000
# 2배 필요
MAX_N = 401 * 2
def BFS(source, sink, visited):
que = deque()
que.append(source)
while que and visited[sink] == -1:
sv = que.popleft()
for dv in graph[sv]:
if capacity[sv][dv] - flow[sv][dv] > 0 and visited[dv] == -1:
visited[dv] = sv
que.append(dv)
if dv == sink:
break
if visited[sink] == -1:
return True
else:
return False
def edmonds_karp(source, sink):
answer = 0
while True:
visited = [-1 for _ in range(MAX_N)]
if BFS(source, sink, visited):
break
min_flow = INF
# 해당 경로의 가장 적은 잔여용량(min_flow) 구하기
dv = sink
while dv != source+1:
sv = visited[dv]
min_flow = min(min_flow, capacity[sv][dv] - flow[sv][dv])
dv = sv
# min_flow 만큼 경로의 유량 증가, 유량 대칭 적용
dv = sink
while dv != source+1:
sv = visited[dv]
flow[sv][dv] += min_flow
flow[dv][sv] -= min_flow
dv = sv
# source에서 sink로 흐르는 전체 유량 적용
answer += min_flow
return answer
N, P = map(int, input().split())
graph = [[] for _ in range(MAX_N)]
capacity = [[0] * MAX_N for _ in range(MAX_N)]
flow = [[0] * MAX_N for _ in range(MAX_N)]
for _ in range(P):
sv, dv = map(int, input().split())
# in, out 구분
sv_in = sv * 2 - 1
sv_out = sv_in + 1
dv_in = dv * 2 - 1
dv_out = dv_in + 1
graph[sv_out].append(dv_in)
graph[dv_in].append(sv_out)
graph[dv_out].append(sv_in)
graph[sv_in].append(dv_out)
capacity[sv_out][dv_in] = 1
capacity[dv_out][sv_in] = 1
# in -> out으로 흐르는 단방향 간선을 모든 정점에 대해 생성
for i in range(1, N+1):
sv = i * 2 - 1
dv = sv + 1
graph[sv].append(dv)
graph[dv].append(sv)
capacity[sv][dv] = 1
print(edmonds_karp(1, 3))