[TIL] 크루스칼 알고리즘

cjkangme·2023년 2월 19일

TIL 알고리즘

Algorithm

목록 보기

13/35

최소 비용 신장 트리 (Minimum Cost Spanning Tree)

최소 비용 신장 트리의 정의는 무방향 가중치 그래프에서 모든 노드를 최소 비용으로 연결하는 간선만을 나타낸 트리를 말한다.

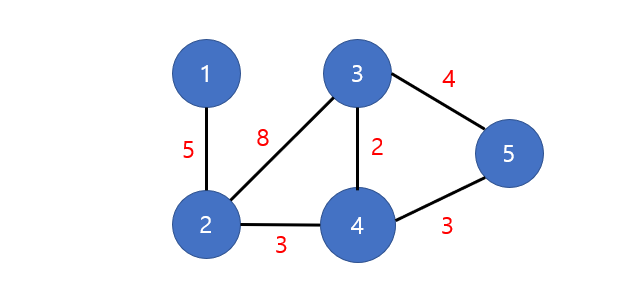
위와 같이 노드와 간선 및 가중치로 구성된 트리가 있다고 하자

여기서 신장 트리(Spanning tree)란 최소의 간선 수를 사용해서 각 노드를 연결한 트리이다.
모든 N개의 노드가 연결되어있을 경우 신장 트리의 간선 수는 N-1개이다.
신장트리는 여러 종류가 존재할 수 있다.

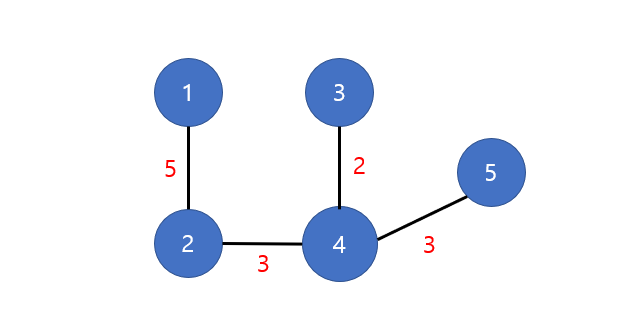
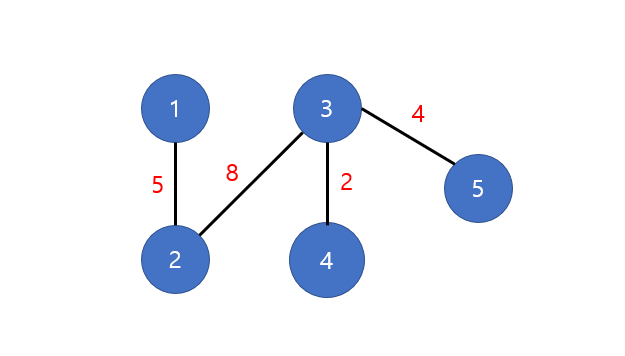
위 두가지는 모두 가능한 신장 트리의 경우이다.

최소 비용 신장 트리는 신장 트리 중 가중치의 합(비용)이 최소가 되도록 간선을 연결한 트리를 말한다.

그림 중 첫번째 신장트리의 총 비용은 13이며, 두번째 신장트리의 총 비용은 19이다.
트리에서 13보다 적은 비용으로 모든 노드를 연결하는 경우는 없으므로, 첫번째 신장 트리가 바로 최소 신장 트리이다.

크루스칼 알고리즘

크루스칼 알고리즘은 바로 무방향 가중치 그래프에서 최소 신장 트리를 찾아내는 알고리즘이다.

여기에 서로소 집합 자료구조라는 것이 이용되는데, 이와 관련해서는 매우 잘 정리해주신 분이 계셔서 해당 블로그 글을 참조하면 좋을 것 같다.

서로소 집합 자료구조 정리

알고리즘 개요

모든 간선을 가중치 기준으로 오름차순 정렬한 뒤,
가중치가 낮은 것부터 꺼내어 해당 간선이 노드를 연결하는데 도움이 되면 트리에 추가하는 방식이다.

여기서 도움이 되는 것의 기준은, 트리가 사이클을 이루지 않는 것이다.
러프하게 설명하면 그래프 내에서 자기들끼리 순환선을 이루는 것을 사이클이라 생각하면 된다.
정확한 개념은 해당 노드의 부모 노드가 동일할 때 사이클을 이룬다.

맨위 그림의 모든 간선을 가중치 기준으로 정렬하면 다음과 같다.

가중치	노드1	노드2
2	3	4
3	2	4
3	4	5
4	3	5
5	1	2
8	2	3

가장 가중치가 낮은 3-4 간선을 꺼내어 연결한다.
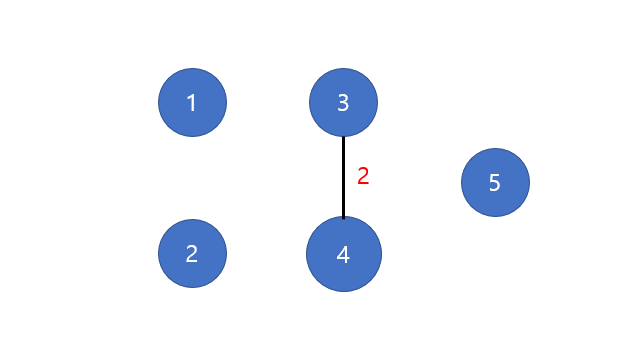
그 다음으로 가중치가 낮은 2-4 간선을 꺼내어 연결한다. (4-5와 순서 바뀌어도 상관 x)
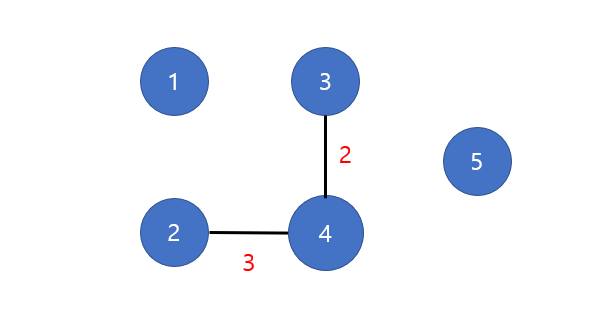
그 다음으로 가중치가 낮은 4-5 간선을 연결한다.
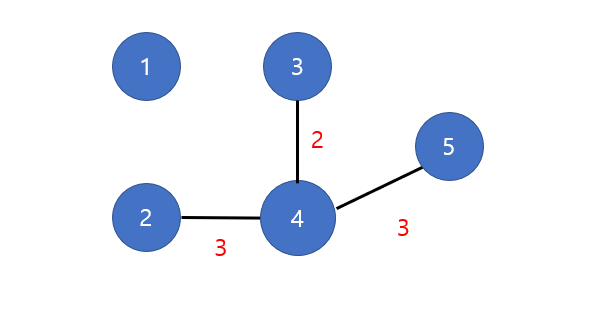
그 다음으로 가중치가 낮은 것은 3-5인데, 이 경우 3-4-5가 사이클을 이루게 된다.

정확히 설명하면 현 시점에서 3, 4, 5의 부모노드는 모두 2로 동일하기 때문에 사이클을 이룬다.

이 경우 3-5 간선은 노드 연결에 기여하지 않으므로 무시하고 다음 순서로 넘어간다 (점선표시)

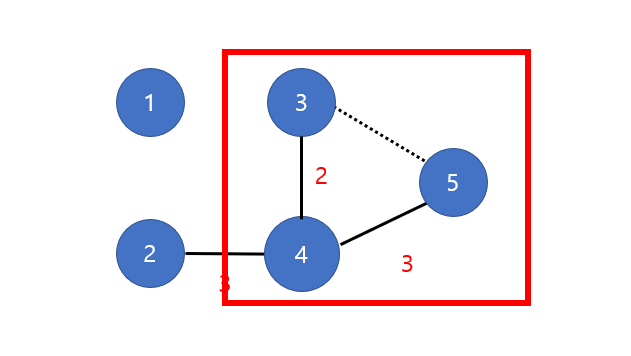
그 다음으로 가중치가 낮은 1-2 간선을 연결한다.

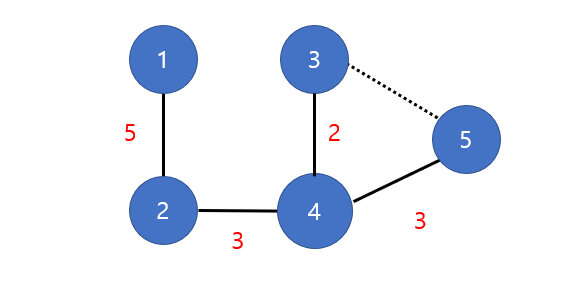
아직 간선이 남았지만 더이상 연결할 필요가 없다.
그 이유는 신장 트리의 간선 수는 항상 N-1개이기 때문이다.
이미 4개의 간선이 있으므로 최소 비용 신장 트리를 찾은 것이다.

알고리즘 절차

0. 서로소 집합 연산 정의

서로소 집합 자료구조에 필요한 find 연산과 union 연산을 정의한다.

def find(parents, x):
    if parents[x] != x:
        parents[x] = find(parents, parents[x])

    return parents[x]


def union(parents, a, b):
    a = find(parents, a)
    b = find(parents, b)

    if a > b:
        parents[a] = b
    else:
        parents[b] = a

find 연산의 경우 부모 노드를 찾는 연산을 수행하면서 자신의 값을 최신화한다.

예를들어 1-2-3-4-5의 계층으로 이루어진 트리가 다음과 같이 저장되어 있다고 가정하자.

노드번호	1	2	3	4	5
부모 노드	1	1	2	3	4

여기서 5를 호출하면
parents[x] = find(parents, parents[x])에 의해 4-3-2-1이 재귀적으로 호출되며 최종적으로 반환된 1을 이용해 자신의 부모 노드 값을 최신화할 수 있다.

노드번호	1	2	3	4	5
부모 노드	1	1	1	1	1

union 연산의 경우 두 간선을 연결할 경우 항상 낮은 번호를 가진 노드를 부모 노드로 취급하도록 했다.

1. 그래프 입력 받기

일반적으로 그래프를 입력받을 때와 달리 연결하는 두 노드와 가중치 정보만을 트리에 추가하면된다.

graph = []
for _ in range(M):
    # a, b : 노드, c : 가중치
    a, b, c = map(int, input().split())
    graph.append((a-1, b-1, c))

2. 정렬하기

가중치 기준 오름차순 정렬한다.

graph.sort(key=lambda x: x[2])

3. for loop & 부모 확인

정렬된 간선을 가중치가 낮은 것 부터 차례대로 꺼낸다.
간선의 연결된 두 노드의 부모가 같은지 확인한다.

부모가 같다면 사이클이므로 아무 액션 없이 다음 간선으로 넘어간다.
부모가 다르다면 해당 가중치를 총 비용에 추가하고 부모를 지정한다.

for a, b, weight in graph:
    if find(parents, a) != find(parents, b):
        answer += weight
        union(parents, a, b)

4. 종료 조건 및 출력

모든 graph를 다 돌아도 결과가 변하지는 않지만,
노드에 비해 간선 수가 많을 경우 연결된 간선이 N-1개에 도달했을 때 for loop을 빠져나오는 것이 효율적일 수 있다.

for a, b, weight in graph:
    if count == N-1:
        break
    if find(parents, a) != find(parents, b):
        answer += weight
        count += 1
        union(parents, a, b)
        
print(answer)