썸네일 메이커

Convolution

Convolution이란

• 두개의 함수를 섞어주는 방법 또는 연산자를 말한다.
• 주로 2D image convolution에 이용한다.

(I * K)(i, j) = Σ(m)Σ(n) I(m, n)K(i-m, j-n) = Σ(m)Σ(n) I(i-m, j-n)K(m, n) = O(i-m, j-n)
I : 전체 이미지 공간
K : 적용하고자 하는 convolution filter(kernel)
O : convolution의 결과로 출력되는 feature map

Convolution 예시

3x3의 필터 K를 사용할 때
O11 = I11K11 + I12K12 + I13K13 + I21K21 + I22K22 + I23K23 + I31K31 + I32K32 + I33K33 + bias

• 만약 3x3 필터의 값이 모두 1/9라면 output의 값은 이미지의 3x3을 평균한 것과 같기 때문에 blur 효과가 발생한다.
• 이 외에도 필터값에 따라 Emboss(강조), Outline(외곽선) 등의 출력이 가능하다.

RGB Image Convolution

• 가로, 세로 32px로 구성된 이미지는 32 x 32 x 3의 tensor가 된다.
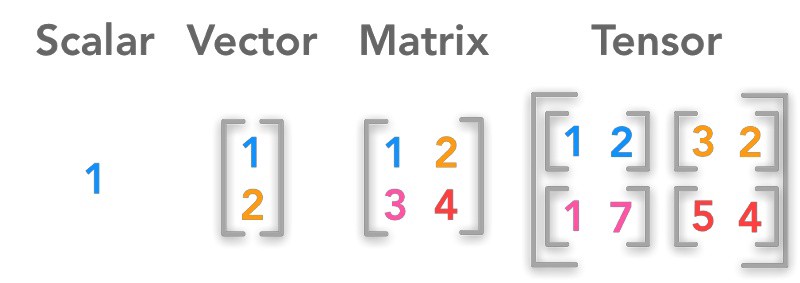
  ※ tensor : 3d 이상의 공간을 배열의 집합으로 나타내는 표기법(자료구조)이다. 3차원 공간에서는 방향과 크기를 나타낸 벡터 3개로 구성된다.
• 여기서 마지막의 3은 RGB를 의미한다.
  

참고자료

• kernel의 깊이는 이미지와 동일해야 한다. kernel의 크기를 5 x 5 x 3이라 했을 경우 28 x 28의 feature map이 출력된다.
• 이 때 kernel을 여러개 사용한다면 그만큼 feature map의 채널이 늘어난다.
• 즉 input 이미지의 채널과 output feature의 채널을 알면 kernel의 크기와 개수를 알 수 있다.

input image가 32 x 32 x 3이고, feature이 28 x 28 x 4라면 kernel은 5 x 5 x 3 4개 이다.

Convolutional Neural Networks(CNN)

Stack of Convolutions

• 신경망에서는 CONV를 거치고 각각의 파라미터에 활성함수를 적용하는 것을 반복하여 층을 깊이 쌓는다.
• 이때 각각의 단계에서 연산에 필요한 파라미터의 숫자를 계산할 수 있어야 한다.

파라미터의 수와 일반화 성능

• 일반적으로 머신러닝에서 학습하고자 하는 parameter가 늘어날수록 학습이 어려운 것은 물론, 일반화 성능이 떨어진다.
• 즉 아무리 학습이 잘 되어도 실제 deploy시 성능이 떨어진다는 것이다.
• 때문에 parameter 숫자를 줄이는 것이 CNN 발전의 방향이다.

CNN의 구조

• convolution layer, pooling layer, fully connected layer로 구성된다.
• convolution layer, pooling layer는 이미지에서 유용한 정보를 뽑아내기 위해 필요하다
• fully connected layer는 classification 등 decision making을 위해 필요하다
  - 파라미터가 가장 많은 부분으로, 점점 최소화되고 없어지는 추세이다.
  

Pooling?

참고자료

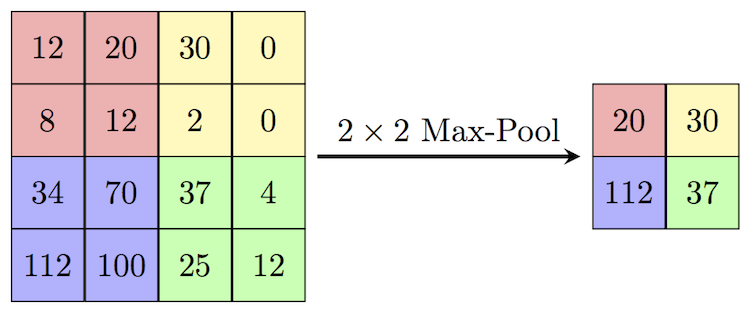
• 강의에서 자세히 다루지는 않는데, 간단히 설명하면 convolution의 결과로 나온 데이터를 보다 작은 크기로 줄이는 방법이다.
• max-pool의 경우 최대값만을 취하는 방법이고, 평균값을 취하는 average-pool이 있다.
• 신경망의 표현력을 줄여 overfitting을 억제하고, 데이터를 줄여 hardware resource를 줄인다는 장점이 있다.

파라미터 계산하기

• CNN 모델을 봤을 때 대략적으로라도 파라미터를 계산할 수 있는 것이 중요하다.
• 이를 위해 알야할 개념을 살펴보자

Stride

• convertion filter를 얼마나 dense하게 찍는지는 표현한다.
• 모든 픽셀마다 데이터를 찍는 것을 Stride = 1이라 한다.
• 한 픽셀을 건너 뛰면서 데이터를 찍는 것을 Strider = 2라 한다.
• 2D image에서는 width, height 두 방향으로 각각 stride를 적용한다.

참고자료

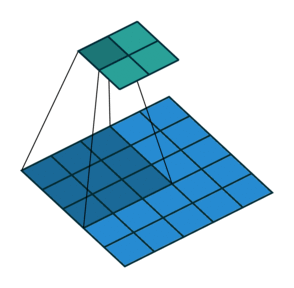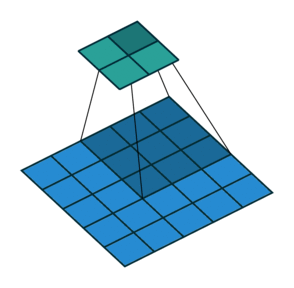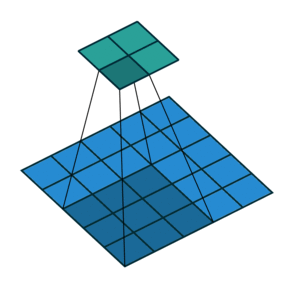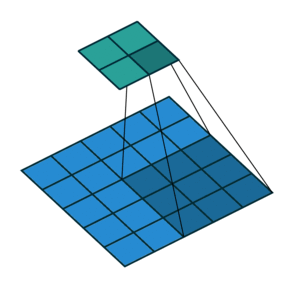
5 x 5 input에 3 x 3 kernel, stride = 2를 적용한 예시

Padding

• input의 boundary 정보가 버려지는 것을 막기 위해 input 가장자리에 추가하는 값이다.
• Zero padding이라 하면 input 가장자리에 0 값을 추가하는 것을 말한다.
• kernel에 맞게 적절한 padding을 사용하면 input의 spatial dimension과 output의 spatial dimension이 동일하게 된다.

참고자료

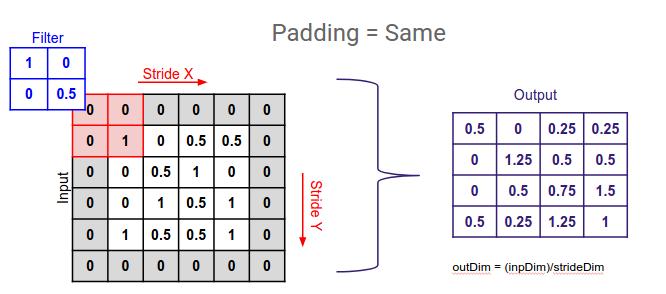
• 3 x 3 kernel의 경우 padding = 1을 적용하면 동일한 spatial dimension을 가진 output feature를 얻을 수 있다.
• 마찬가지로 5 x 5라면 2, 7 x 7이라면 3을 적용하면 된다.

직접 계산해보기

GoogLeNet 논문

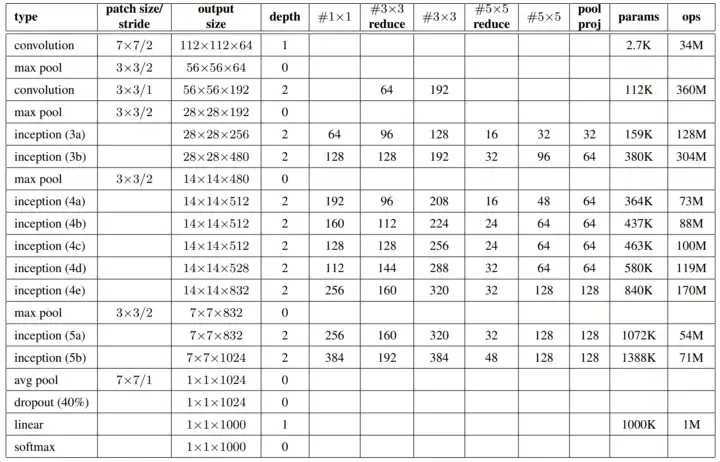
두번째 convolution

• kernel의 크기는 3 x 3, input 채널은 64개 output의 채널은 192개이므로

3 3 64 * 192 = 110,592 ≒ 110K

• 다음과 같이 파라미터를 계산할 수 있다.

1 x 1 convolution

• kernel의 크기가 1x1인 convolution으로 spatial dimension은 유지한 채 채널을 줄여 파라미터 숫자를 줄이는 방법이다.
• convolution layer을 깊이 쌓으면서도 parameter를 줄일 수 있어 굉장히 자주 사용된다.