벡터 연산, 행렬 연산,

내적 (inner product)

점곱(dot product)이라고 부르기도 한다.

표기법

$a \cdot b = <a, b> = a^Tb = \left | a \right | \left | b \right | \cos{\theta} = \sum{a_k b_k}$

• 내적하는 두 벡터의 길이(성분 갯수)가 같아야 한다.
• 내적의 결과는 하나의 스칼라이다.
  • $\sum{a_k b_k}$에서 알 수 있듯이, 서로 대응하는 성분끼리 곱한 뒤 이를 모두 합하여 하나의 값으로 만든다.
• 자기자신과의 내적은 자신의 벡터 크기의 제곱과 같다. $a \cdot a = \left \| a \right \|^2$
• 내적은 교환 법칙, 분배 법칙이 성립한다. 그러나 결합 법칙은 성립하지 않는다.
  • 결합 법칙이 성립하지 않는 것은 두 벡터의 내적 결과가 스칼라라는 것에서 쉽게 유추할 수 있다.
• $\left | a \right | \left | b \right | \cos{\theta}$에서 알 수 있듯이, 서로 수직인 벡터를 내적하면 $0$이다.
• 내적을 통해 두 벡터간의 각도를 계산할 수 있다.
  • $\theta = cos^{-1}\frac{a \cdot b}{\left | a \right | \left | b \right |}$

외적 (outer product)

표기법

$a \otimes b = ab^T = \begin{bmatrix} a_0b_0 & a_0b_1 & \cdots & a_0b_{n-1} \\ a_1b_0 & a_1b_1 & \cdots & a_1b_{n-1} \\ \vdots & \vdots & \vdots & \vdots \\ a_{n-1}b_0 & a_{n-1}b_1 & \cdots & a_{n-1}b_{n-1} \end{bmatrix}$

• 성분이 m개인 벡터 a와 성분이 n개인 벡터 b에 대해 외적하였을 때, (m x n) 행렬이 결과로 나온다.
• 성분들의 모든 조합을 나열한다는 특징이 있어, 서로 다른 vector를 혼합할 때 쓰일 수 있다.

벡터곱 (vector product)

가위곱 (cross product)이라고 부르기도 한다.

외적, 벡터곱이 앞서 말한 outer product와 동일한 의미로 사용되는 경우가 있어 주의가 필요하다.

여기서 말하는 벡터곱은 3차원 유클리드 공간에서의 연산이며 연산 결과가 벡터이다.

$a \times b =\hat{n} \left | a \right | \left | b \right | \sin{\theta} = [a_1b_2 - a_2b_1, a_0b_2 - a_2b_0, a_0b_1 - a_1b_0]$

• $\hat{n}$은 두 벡터에 모두 수직인 단위 벡터이다.
• 두 벡터가 서로 같은 방향(평행)일 때 영벡터, 서로 수직일 때 최댓값을 갖는다.

행렬곱

말 그대로 행렬간의 곱셈을 말한다.

행렬곱의 성질

• $A(BC) = (AB)C$ → 결합 법칙 성립
• $A(B+C) = AB + AC, (A+B)C = AC + BC$ → 분배 법칙 성립
• $AB \neq BA$ → 교환 법칙이 성립하지 않음
• $(n \times m)(m \times k) = (n \times k)$
  • 앞 행렬의 열 갯수, 뒷 행렬의 행 갯수가 같아야 연산할 수 있다.

내적과 외적의 행렬 곱셈 표현

벡터는 행벡터(n x 1), 열벡터(1 x n)로 나타낼 수 있기 때문에 이를 이용해 행렬곱으로 내적과 외적을 표현할 수 있다.

• 내적 : $a^Tb = (1 \times n)(n \times 1)$
• 외적 : $ab^T = (n \times 1)(1 \times m)$

앞서 보았던 내적, 외적의 규칙이 그대로 성립하는 것을 볼 수 있다.

정방 행렬

기하학적 관점에서 행렬곱은 일종의 함수로 한 공간의 점을 다른 공간의 점으로 변환하는 수단이라 할 수 있다.

그 중 정방행렬은 (n x n) 형태의 행과 열의 갯수가 같은 행렬로, 한 점을 같은 공간 내에 투영하는 역할을 한다고 볼 수 있다.

예를 들어 아핀 변환은 정방행렬의 행렬곱과 병진 이동으로 표현할 수 있다.

• $y = Ax + b$
  
  ${\displaystyle {\begin{bmatrix}x\\y\end{bmatrix}}\mapsto {\begin{bmatrix}0&1\\2&1\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}+{\begin{bmatrix}-100\\-100\end{bmatrix}}}$
  출처: 위키피디아 - Affine Transformation

행렬식 (determinant)

행렬식은 정방행렬을 하나의 스칼라 값으로 사상하는 함수이다.
행렬식은 행렬의 고유값을 계산하는데 사용하거나, 벡터곱을 간단히 표현하는데 사용되기도 한다.

$det(A) = \begin{vmatrix} a_{00} & a_{01} & a_{02}\\ a_{10} & a_{11} & a_{12}\\ a_{21} & a_{22} & a_{23} \end{vmatrix} \in \mathbb{R}$

행렬식의 주요 성질

1. 모든 성분이 0인 행이나 열이 존재하면 $det(A) = 0$이다.
2. 동일한 두 행이 존재하면 $det(A) = 0$이다.
3. 삼각행렬, 대각행렬일 경우 행렬식의 결과는 주대각 성분의 부분곱($\Pi{a_{ii}}$)이다.
4. $det(I) = 1$
5. $det(A)det(B) = det(AB)$
6. $det(A) = det(A^T)$

역행렬 (inverse matrix)

역행렬은 정방행렬에 대한 역원을 말한다.
즉 행렬에서 역행렬은 연산한 결과가 항등 행렬일 때의 상대쪽의 행렬을 말한다.

• $AA^{-1} = A^{-1}A = I$
• 행렬식을 통해 역행렬의 존재 여부를 알 수 있다.
  • $det(I) = 1$
  • $det(A)det(A^{-1}) = det(AA^{-1}) = 1$
  • $\therefore det(A) = \frac{1}{det(A^{-1})}$
  • 즉 $det(A)=0$일 때 위 방정식이 성립하지 않으므로, det(A)=0일 때 A의 역행렬이 존재하지 않는다.

대각행렬의 역행렬은 각 주대각성분에 역수를 취한 것과 같다.

고유값과 고유벡터

영벡터가 아닌 정방행렬에 의해 투영된 벡터를 $v' = Av (v \neq 0)$라고 할 때,
한 스칼라 값 $\lambda$에 대해 다음의 방정식을 만족할 경우 행렬 A에 대한 고유벡터를 구할 수 있다.

• $Av = \lambda v$
  • $v$: $A$에 대한 고유벡터(eigenvector)
  • $\lambda$: 교유벡터에 대한 고유값(eignevalue)

어떤 행렬에 대한 고유벡터는 여러개 있거나 아예 없을수도 있다.

고유값과 고유벡터 구하기

$\lambda$는 스칼라이므로, 방정식을 풀기 위해 단위 행렬을 곱해 $A$와 동일한 크기의 정방행렬로 만들 수 있다.

• $Av = \lambda I v → (A - \lambda I)v = 0$

즉 영벡터가 아닌 벡터 $v$를 영벡터로 사상되게 하는 $(A - \lambda I)$가 존재해야한다.
이 조건을 만족하기 위해서는 $(A - \lambda I)$의 역행렬이 존재하지 않아야 한다. 즉, $det(A-\lambda I) = 0$일 때 고유벡터와 고유값이 존재한다.
역행렬이 존재할 경우 $(A - \lambda I)^{-1}(A - \lambda I)v = 0 → v=0$이 되어 $v$가 영벡터일 때만 식이 성립하게 되기 때문이다.

이를 이용하여 아래의 방정식을 만들 수 있다.

• $A - \lambda I = \begin{bmatrix} a-\lambda & b \\ c & d-\lambda \end{bmatrix}$
• $det(A-\lambda I) = (a-\lambda)(d-\lambda) - bc = 0$

삼각행렬, 대칭행렬에서는 주대각 성분이 곧 고유값이 된다. (행렬식이 주대각 성분의 부분곱이기 때문)

근 $\lambda$를 알았다면, 다시 첫번째 식에 대입하여 고유벡터 $v$를 구할 수 있다.
이렇게 구한 고유벡터는 주성분 분석(PCA) 등, 머신러닝/딥러닝에서 자주 쓰인다.

공분산 행렬(Covariance matrix)

공분산 행렬은 여러 특징(열)을 갖는 여러 데이터(행)로 구성된 행렬에서, 각 특징이 서로 어떤 관계를 갖는지를 분산으로 나타내는 행렬이다.

n x m 행렬의 공분산 행렬은 m x m의 정방행렬이다.

• $\sum_{ij} = \frac{1}{n-1}\sum_{k=0}^{n-1}{(x_{ki} - \bar{x_i})(x_{kj} - \bar{x_j})}$
  • i, j는 비교하는 각 특징을, k는 k번째 성분임을 나타낸다.
  • i = j일 때 $(x_{ki} - \bar{(x_i)}$이므로 특징 i의 분산(불편추정량)이 된다.
  • i = j일 때 공부산 값은 특징 i, j에 대해 한 변수가 변할 때 다른 변수가 어떠한 연관성을 갖고 변하는지를 나타낸다.

공분산 행렬 역시 주성분 분석(PCA)에서 사용되는 등, 머신러닝/딥러닝에서 자주 쓰인다.

주성분 분석(Principal Component Analysis, PCA)

주성분 분석은 데이터가 어느 방향으로 흩어져 있는지를 파악하기 위한 기법이다.
머신러닝/딥러닝에서는 고차원 raw 데이터의 차원을 줄이면서 서로 독립적인 성분으로 변환하기 위해 사용한다.

주성분 (Principal Component)

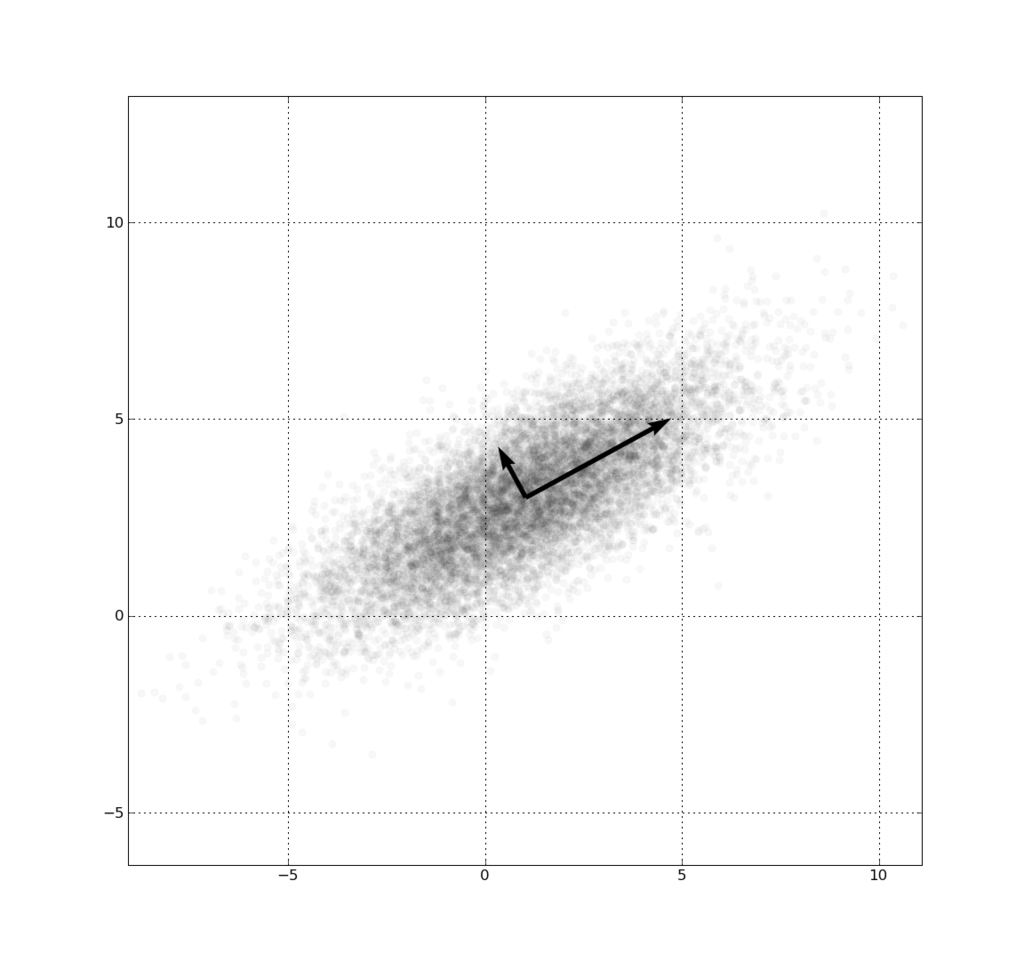
출처 : 위키피디아

주성분은 데이터 집합에서 데이터들이 길게 흩어져 있는 방향을 나타낸다.

데이터(벡터)를 하나의 축으로 사상했을 때, 가장 길게 늘어지는 방향이 첫번째 주성분이 되고, 첫번째 주성분과 직교하면서 두번째로 길게 늘어지는 방향이 두번째 주성분이 된다.

즉 각각의 주성분은 이전에 구한 모든 주성분과 직교한다.

주성분 분석의 의의

앞서 말했듯 주성분 분석은 데이터 집합의 차원을 줄이기 위해 주로 사용되는데, 100차원의 데이터에서 주성분 2개가 데이터 산포의 대부분을 설명한다면, 데이터(벡터)를 두 주성분 축을 따라 직교 변환하는 것으로 충분히 데이터를 특징잡을 수 있게 된다.

즉 훨씬 더 적은 차원(적은 메모리)으로 데이터를 나타낼 수 있게 된다.
또 주성분은 서로 독립적이기 때문에 머신러닝에서 다중공선성 문제를 해소할 수 있다.

주성분 분석 과정

1. 데이터 집합을 mean centering한다. ($x_{ij} - \bar{x}_i$, 특징별로 각 관측값에서 평균을 빼는 연산 과정)
2. 평균 중심화된 데이터의 공분산 행렬 $\Sigma$를 구한다.
3. $\Sigma$의 고유값, 고유벡터를 구한다. 공분산 행렬은 항상 대칭행렬이므로 공분산 행렬의 주대각 성분, 즉 특징별 분산이 고유값이 된다.
4. 고유값을 내림차순 정렬한다.
5. 가장 작은 고유값, 고유벡터를 폐기한다 (생략 가능)
6. 나머지 고유벡터들로 변환행렬 W를 만든다.
7. 변환 행렬을 기존 데이터 집합에 적용해 새 데이터 집합 $x' = Wx$를 구한다. 이렇게 구한 새 데이터 집합의 변수를 파생 변수라 부른다.
8. 위 과정을 원하는 차원이 될 때까지 반복한다.

• 주성분 분석에서 주의할 점은 분산을 탈락한 성분이 분산에 대한 기여도는 낮아도, 실제로는 데이터의 특징을 분류하는 중요한 성분일 수도 있다는 것이다. 때문에 충분한 실험으로 주성분 분석 전후 결과를 비교해야 한다.