강의 주소 : https://www.boostcourse.org/ai251/lecture/540315?isDesc=false

Recap

• Ax = b의 선형 방정식에 대해 선형결합 강의에서 b가 재료벡터로 이루어진 span에 포함될 경우 해가 존재한다는 것을 배웠다.
• 그렇다면 해가 하나만 존재한다(unique 하다)는 것은 어떻게 알 수 있을까?

Uniqueness of Solution

• 결론부터 말하자면 각각의 재료벡터가 모두 선형독립(linearly independent)이라면 해가 하나만 존재(unique)한다.
• 반대로 선형의존(linearly dependent)이라면 해는 무수히 많이 존재한다.

선형독립의 정의

Practical Definition

• p개의 벡터에 대해 1, 2, 3, ... ,j 번째까지 span을 벡터를 하나씩 추가해가며 구한다고 생각해보자.
• 이 때, j번째 벡터가 이전의 벡터(1, 2, 3, ..., j-1번째)로 구한 span에 포함된다면, 벡터를 추가하여도 span의 공간적 범위는 늘어나지 않는다.
• 이러한 벡터가 적어도 하나 이상 존재한다면, p개의 벡터로 이루어진 집합은 선형의존이라 한다.
• 이러한 벡터가 하나도 없다면, 선형독립이라 한다.

• 이를 그림으로 풀어 설명하면 다음과 같이 된다.

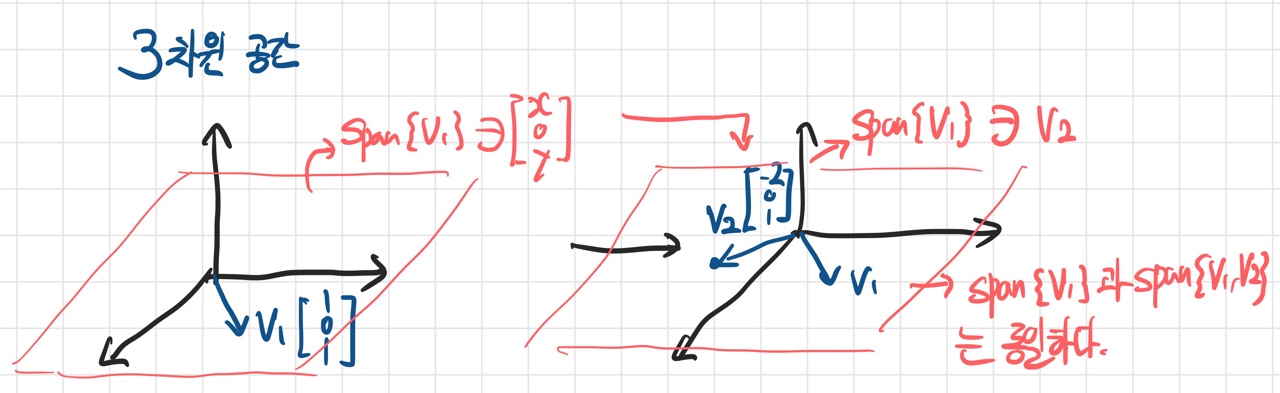
• 위 그림에서 2번째 벡터v2는 v1 벡터의 span에 포함되므로 span의 공간적 범위는 늘어나지 않고, {v1, v2}는 선형의존이다.

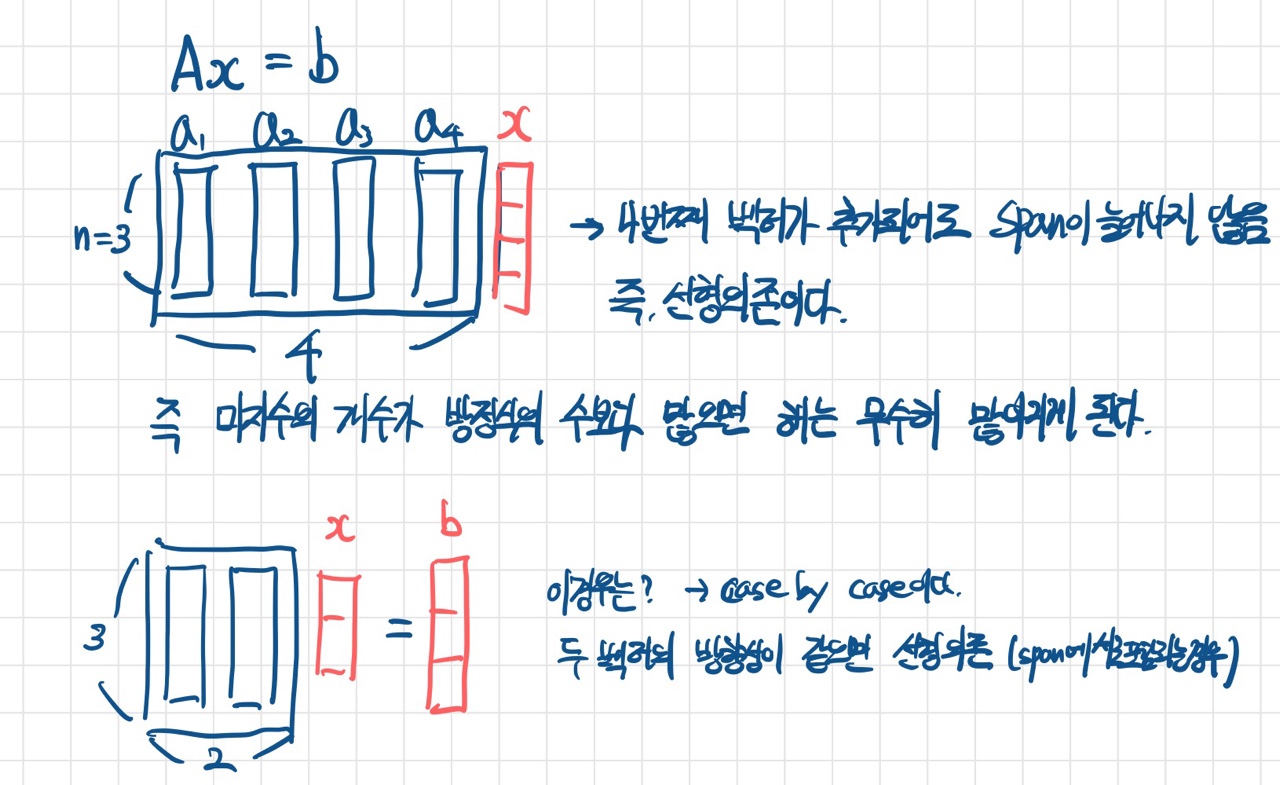
• 미지수가 4개(=재료벡터가 4개)이고, 방정식의 수(재료벡터의 차원)가 3개라고 가정하자.
  • 3개의 재료벡터로 이루어진 span은 3차원 공간 전체집합과 같으므로, 4번째 재료벡터가 3차원인 이상 어디에 벡터가 추가되어도 span이 늘어나지 않게 된다. 이 경우 무조건 선형의존이라 할 수 있다.

Formal Definition

• b = 0(영벡터)이라고 가정할 경우 벡터 방정식은 다음과 같다.

• 이 때, 모든 계수가 0이라는 해가 무조건 하나 존재하게 된다.
• 이 해를 trivial solution(자명해)이라 한다.
  • trivial은 '하찮은, 사소한'이란 뜻인데, 해가 0이라는게 너무나 당연(자명)해서 사소하게 느껴지는 해라는 의미이다.

• 만약 해가 trivial solution만 존재한다면 선형독립일 것이다.
• trivial solution외의 해, 즉 xi가 하나라도 0이 아닌 해(nontrivial solution)가 존재한다면 선형의존일 것이다.

Nontrivial Solution의 조건

• 결론부터 말하면, 서로 상쇄되어 0벡터로 가는 성분 조합이 존재한다면 nontrivial solution이 존재하고, 선형의존이다.

• nontrivial solution이 존재하는 조건을 다음과 같이 설명할 수 있다.
  

• v1을 상쇄하여 0벡토로 가기 위해v2, v4를 사용할 수 있다.
  

• 즉 다음과 같은 nontrivial solution이 존재한다.
  

• 이를 다음과 같은 수식으로 표현할 수 있다.
  

b ≠ 0 일때도 성립할까?

• 어떤 벡터 방정식에 대해, 다음과 같은 해가 있다고 가정하자.
  
• 이때 재료벡터의 각 성분이 앞서 구했던 0벡터를 만족하는 조합과 같다면 다음과 같이 표현할 수 있다.
  * 오타 : 6v2가 아니라 6v3이다.
  
• 즉 다음과 같은 another solution이 존재한다.
  

결론

• 재료벡터가 linearly independent 할 때 벡터 방정식의 solution은 unique하다.
• nontrivial solution이 존재하지 않을 때 linearly independent하다고 할 수 있다.