
Linear Combinations(선형결합)
- n차원 벡터 p개에 p개의 계수(가중치)를 각각 곱한 것을 더하여 새로운 n차원의 벡터를 얻는 것을 말한다.
Vector Equation
- Linear system의 행렬 방정식을 벡터 방정식으로도 나타낼 수 있다.
행렬 방정식
Ax = b
벡터 방정식
- 위와 같이 나타낸 형태를 벡터 방정식이라한다.
- 그렇다면 벡터 방정식에서 해가 있는지 없는지는 어떻게 확인할 수 있을까?
Span
- 유한한 개수의 재료벡터(벡터 방정식에서 계수 a에 해당)로 만들 수 있는 가능한 모든 선형 결합 결과의 집합을 말한다.
- 결과적으로 벡터 방정식의 결과 b가 a의 span 공간안에 있다면 그 벡터 방정식에는 해가 있다고 할 수 있다.
span의 기하학적 의미
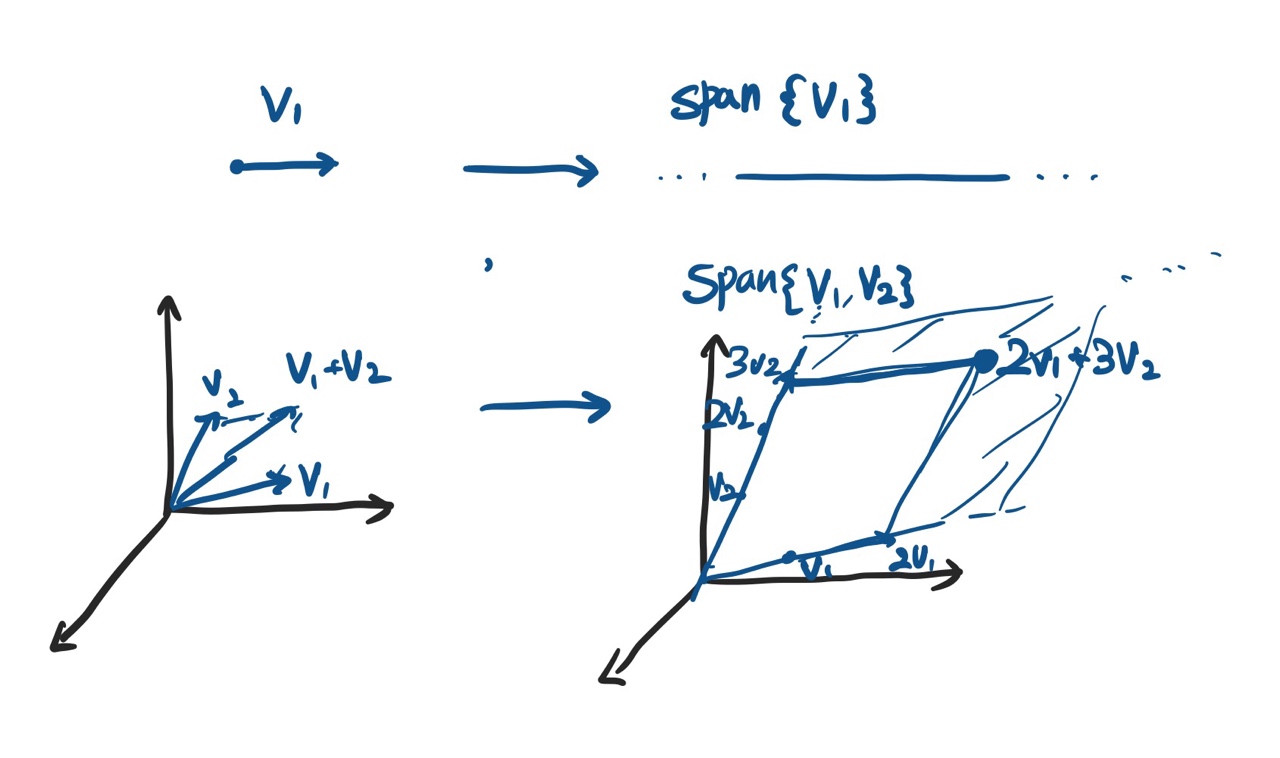
- 재료벡터가 1개라면, span은 하나의 무한한 line이 된다.
- 재료벡터가 2개라면, span은 하나의 무한한 2D 평면이 된다.
- 재료벡터가 3개라면, span은 3차원 공간 전체 집합이 된다. (하지만 4차원 공간의 일부이다)
- 즉 b의 차원이 재료벡터의 개수와 같다면, b는 재료벡터의 span의 어느 한 점에 위치한다는 뜻이고, 이는 해가 있음을 의미한다. (행렬 방정식에서
n=m이고 역행렬이 존재하는 상황과 같다)
행렬곱의 표현
- 행렬곱을 이해하는 시각에는 4가지가 있다.
XY = A
1. 내적
- 행렬간의 곱셈은 기본적으로 두 행렬간의 내적으로 정의할 수 있다.
2. Column Combinations
- 왼쪽의 행렬이 base, 오른쪽의 행렬이 가중치(coefficients)가 되는 선형 결합으로 생각할 수 있다.
3. Row Combinations
- 열벡터를 transpose하면 행벡터가 되므로 행벡터간 선형 결합으로도 행렬곱을 나타낼 수 있다.
- 이 경우 왼쪽의 행렬이 가중치(coefficients), 오른쪽 행렬이 base가 된다.
4. Sum of Rank-1 Outer Products
- 머신러닝에서 중요하게 다루는 개념으로, 외적의 합으로 행렬곱을 나타낼 수 있다.
- 이 강의에서 자세히 다루지는 않았지만, 이 개념은 Low rank factroization과 Covariance matrix(공분산 행렬) 등에서 matrix를 나타내는데 중요하게 쓰인다.
이번 강의의 핵심
- 행렬간의 곱연산을 vector간의 선형 결합을 통해 한번에 표현할 수 있다는 것을 이해
- span의 개념 이해













